1.基本介绍

主串：形如 “hello world”的字符串作为一个整体

子串：上面主串的一部分如“world”

在计算机世界，主串找子串的模式很常见，比如要在word文件中找一句指定的话，那么面对海量的信息，我们匹配算法也有不断的优化，本文会介绍不同的匹配算法和给出对应的代码实现。

模式串：要在主串中找子串的那个字符串。

2.简单匹配--BF算法（暴力搜索）

1.实现

主串为n，子串为m。用一个下标，指向主串并且遍历，依次对应字串的字符，如果不同则指针往下走；如果相同则判断下一个字符是否相同，如果能匹配返回下标，不匹配返回0。（这里的字串开头下标为1，所以0下标没有用来存储数据）

1.如果不匹配，i要变成i-j+2，也就是i和j都遍历的原先位置的下一个；

2.匹配，则i++，j++；

3.如果j走到最后，则说明最后j大于T._len，那么返回的i原先的值；即为i-T._len；

4.不匹配，则直接return 0；

struct String
{
	char* _ch;
	size_t _len;
};//ch中的ch[0]位置不存放东西

//S为主串，T为子串
int Index(String S, String T)
{
	int i = 1, j = 1;
	while (i <= S._len && j <= T._len)
	{
		//判断不匹配，i需要回到原来的位置的后一个
		if (S._ch[i] != T._ch[j])
		{
			i = i - j + 2; //i-j+1得到的是原先的i位置，再+1
			j = 1; //
		}
		//匹配，下面再对比
		else
		{
			i++;
			j++;
		}
	}
	if (j > T._len)
		return i - T._len; // 返回i原先的位置
	return 0;  //走到这里说明没有，返回0
}

2.分析

前提条件：S有n个，T有m个

最坏的情况：每个字串都检查了m次，一共检查了n-m+1次，那么其复杂度为O(nm)

最好情况：只要检查一次，对比了m个数据，那么其复杂度为O(m)

2.KMP算法

1.引入

分析为什么BF算法如此之墨迹

1.BF之所以慢的核心点其实是i是依次遍历的，j也是依次遍历的

2.而之所以ij都依次遍历，其实该算法是将元素一视同仁了，在这套算法下，主串不管是什么都不会影响算法的走向

3.就是这种一视同仁的思想，以至于i跟j对比遍历过，一旦对比失败，i又回溯到前面遍历过的位置，已知晓的信息又变成了未知的东西

4.但是那些遍历过的信息何尝不是一种可以用来处理优化算法的东西呢？i不回溯，前面的信息保留，j也可以通过保留的信息知道哪些东西是不需要再遍历一次，直接往后到需要的位置处。

5.那么KMP的核心就是i不回溯，j通过之前i遍历的信息，省略一些遍历直接匹配有效要匹配的位置跟i的字符进行比较

6.那么现在的问题就变成了，怎么得知这些有效信息，以及如何保存呢？ -- 其实是next数组来解决该问题的

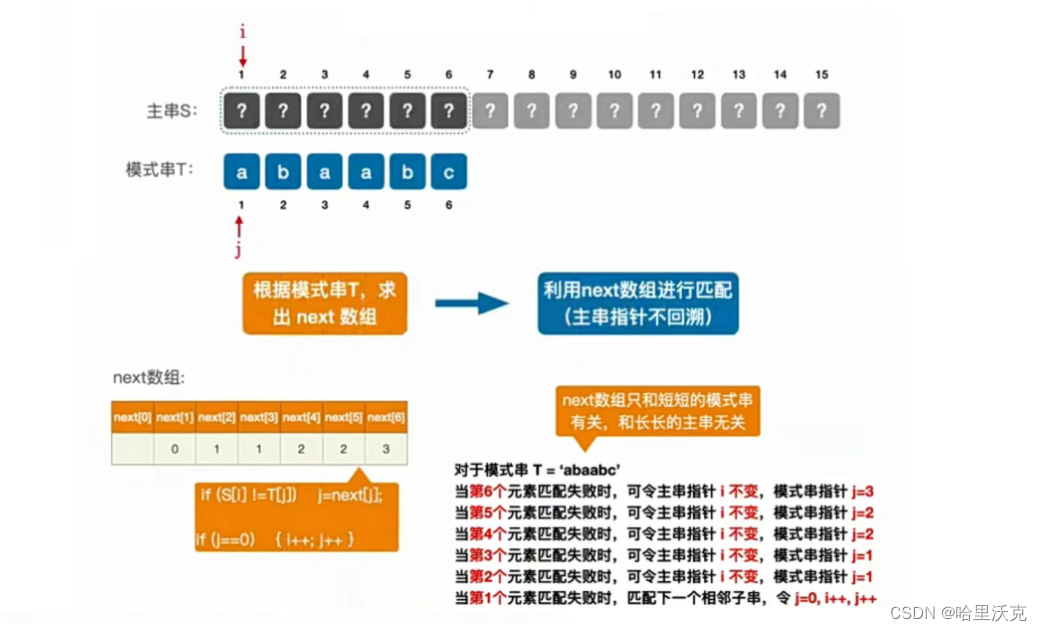
2.next数组理论

其中心思想就是：当字串的第j位置不匹配时，要怎么移动子串和主串的i（不回溯）重新对比

用例子更好说明，直接看图

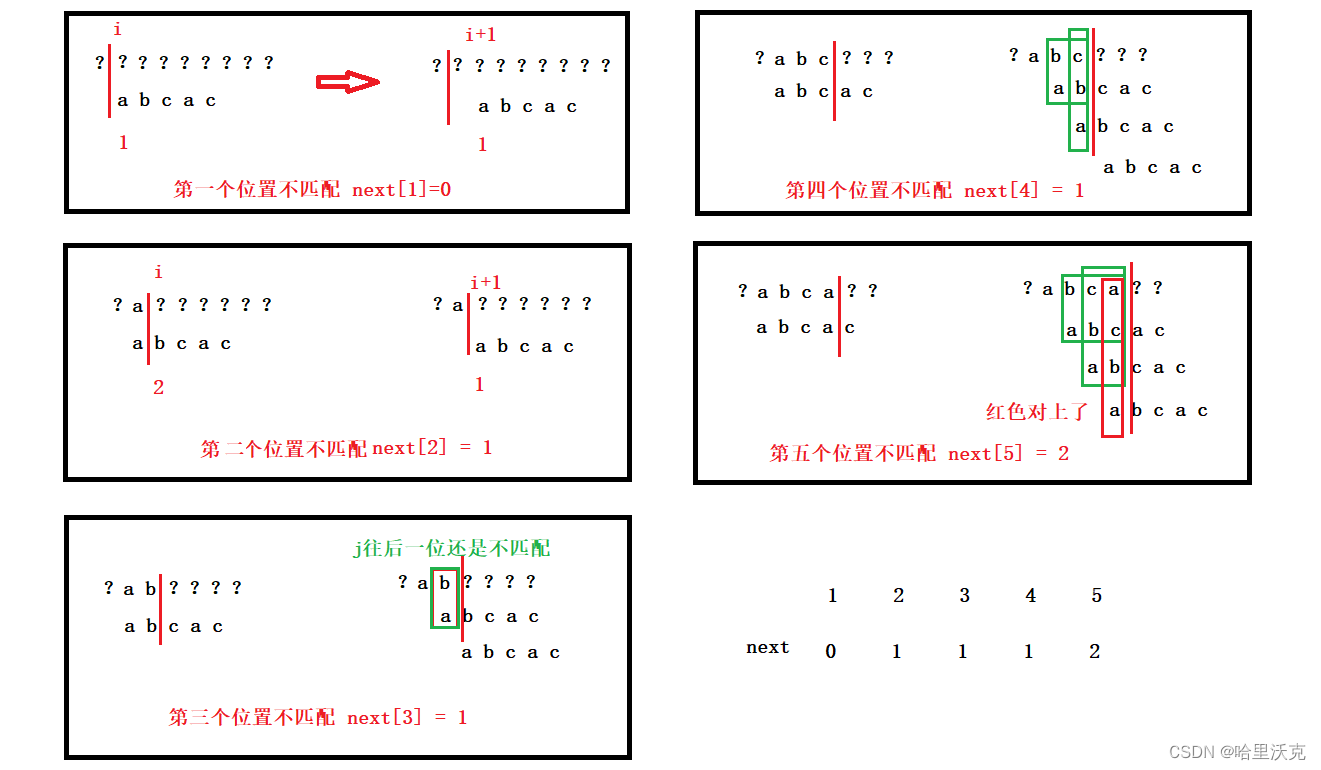
3.优化next数组

本质就算next数组中的指向下标对应的字符和next位置的字符是否相等

1.相等，说明了其实两个等价，既然next位置都对不上，那指向的那个字符跟next位置字符一样，说白了不还是一样对不上吗，所以可以直接替换成next所指位置的next值

2.不相同，则无法优化

if(ch[ next[ j ] ] == ch[ j ]) ------- next[ j ] =next[ next[ j ] ]

4.next数组实现

为了得到next数组，我们需要一些基础的定义：

前缀：以aacfd为例子，{a，aa，aac，aacf}都是前缀，不包含为尾字母

后缀：以aacfd为例子，{d，fd，cfd，acfd}都是后缀，不包含为头字母

最长相等前后缀：以aacfd为例子，都对不上，所以最长相等前后缀为0

前缀表：指前缀的最长相等前后缀对应的表

{a --> 0，aa  --> 1，aac --> 0，aacf --> 0}

此时，前缀表就是一种next表

1.某个位置的字符不匹配，前一个字符需要得到最长相等前后缀

2.最长相等前后缀意味着，在该字符的前缀长度为2跟自己相互匹配，那反映到主串也是一样（换句话说，主串的前缀和子串的后缀相等的最长数都不需要比较了，因为相同，我们只要比较子串的后一个位置即可），那么我们要跳到与之匹配的下一个进行判断

前缀表所有元素往后移，第一位为-1，最后全体+1，这样得到的就是最上面原始的next数组

// next数组，s为子串
void GetNext(int* next, string s)
{
	int i, j;
	//1.初始化
	j = 0; //j为前缀末尾，j最后也是放入next数组的值
	next[0] = 0;

	for (i = 1; i < s.size(); i++)
	{
		while (j >= 0 && s[i] != s[j])
			j = next[j - 1];
		if (s[i] == s[j])
			j++;
		next[i] = j;
	}
}