数据结构 | 排序 - 总结

news2025/4/5 9:06:07

排序的方式

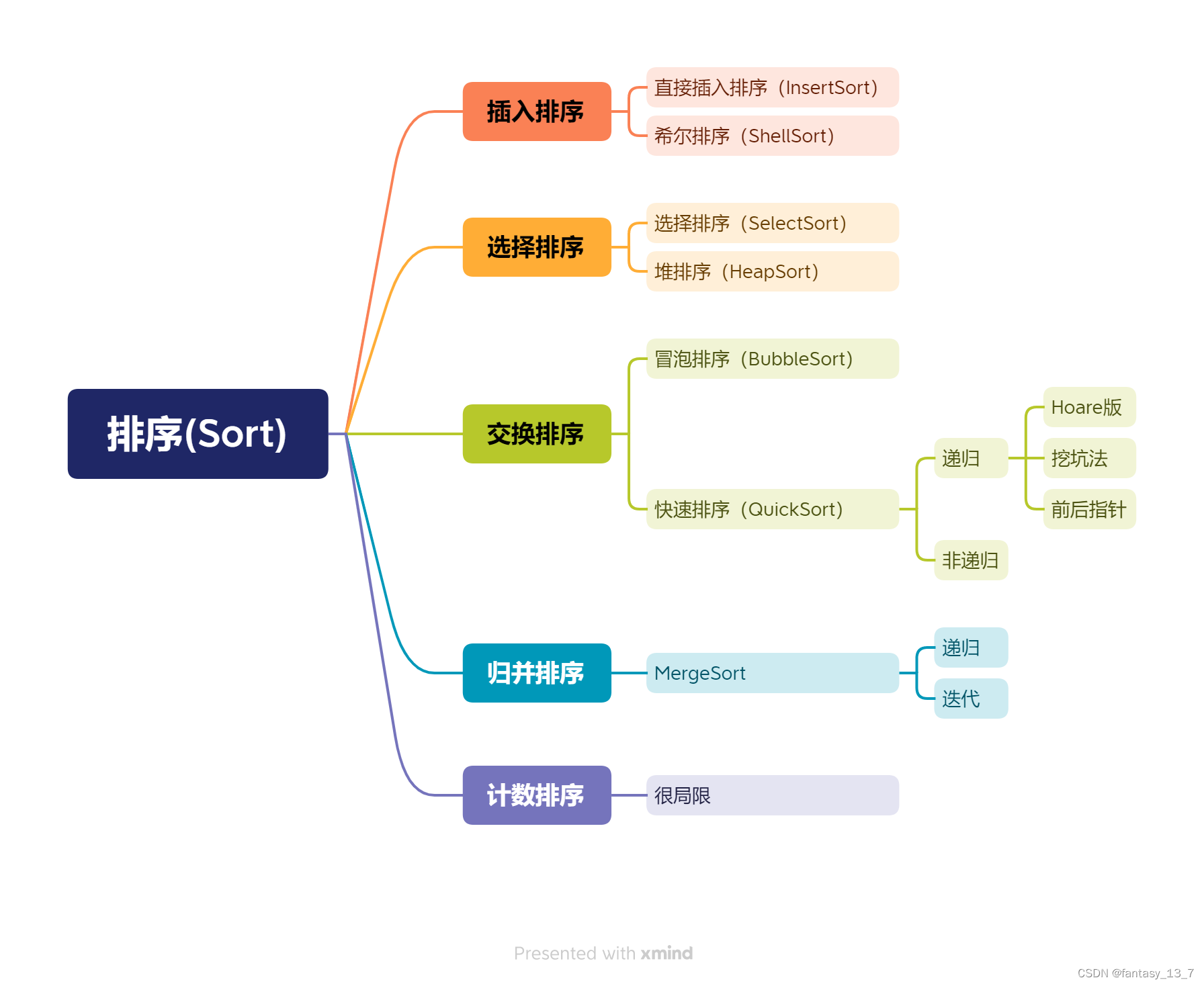
在这里插入图片描述

排序的稳定性

  • 什么是排序的稳定性？
    不改变相同数据的相对顺序

  • 排序的稳定性有什么意义？

    • 假定一个场景：
      一组成绩：100，88，98，98，78，100（按交卷顺序排列，先交在前）
      先需要对这组数据按降序排列，如果分数相同，先交卷的排在前面。

在以上这种场景下，选择具有稳定性的排序方式就很有必要。

排序方式分析比较汇总

排序方式时间复杂度空间复杂度稳定性
InsertO(N2)O(1)√
ShellO(N1.3)O(1)×（预排序相同数可能分到不同组）
SelectO(N2)O(1)×（9,9,4,4）(swap(4,9)后4和4的相对顺序改变)
HeapO(N*logN)O(1)×
BubbleO(N2)O(1)√
QuickO(N*logN)（大量重复数据：N2）O(logN)(递归调用栈帧)×（最后相遇那下交换会打乱）
MergeO(N*logN)O(N+(logN) )√
CountO(N+range)O(range)×

912.排序数组 - 力扣（LeetCode）

👉题目链接

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

//栈
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
	STDataType* _a;
	int _top;		// 栈顶
	int _capacity;  // 容量 
}Stack;
// 初始化栈 
void StackInit(Stack* ps)
{
	STDataType* tmp = (STDataType*)malloc(4 * sizeof(STDataType));
	if (!tmp)
	{
		perror("malloc fail");
		exit(-1);
	}
	ps->_a = tmp;
	ps->_top = 0;
	ps->_capacity = 4;
}
// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
	if (ps->_capacity == ps->_top)
	{
		STDataType* tmp = (STDataType*)realloc(ps->_a, 2 * ps->_capacity * sizeof(STDataType));
		if (!tmp)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->_a = tmp;
		ps->_capacity *= 2;
	}
	ps->_a[ps->_top] = data;
	ps->_top++;
}
// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	assert(ps->_top);

	ps->_top--;

}
// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);
	assert(ps->_top);
	return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->_top;
}
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->_top == 0;
}
// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->_a);
	ps->_capacity = ps->_top = 0;
	ps->_a = NULL;
}


//插入排序
void InsertSort(int* a, int n)
{
	assert(a);
	for (int i = 1; i < n; i++)
	{
		int tmp = a[i];
		int end = i - 1;
		while (end >= 0)
		{
			if (a[end] <= tmp)
			{
				break;
			}
			//a[end + 1] = a[end--];???为什么错误
            a[end + 1] = a[end];
            end--;
		}
		a[end + 1] = tmp;
    }

}

// 希尔排序
void ShellSort(int* a, int n)
{
	assert(a);

	int gap = n / 2;
	while (gap)
	{
		for (int i = 1; i < n; i++)
		{
			int tmp = a[i];
			int end = i - gap;
			while (end >= 0)
			{
				if (a[end] <= tmp)
				{
					break;
				}
				a[end + gap] = a[end];
				end -= gap;
			}
			a[end + gap] = tmp;
		}
		gap /= 2;
	}
}

void Swap(int* x, int* y)
{
	assert(x && y);
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

// 选择排序
void SelectSort(int* a, int n)
{
	assert(a);
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		int mini = begin, maxi = end;

		//[begin+1,end-1]
		for (int j = begin; j <= end; j++)
		{
			if (a[j] < a[mini])
				mini = j;
			if (a[j] > a[maxi])
				maxi = j;
		}
		//swap之前 min==a[mini]  max==a[maxi]
		Swap(&a[begin], &a[mini]);
		//swap之后:begin → min ; mini → original-a[begin]
		//if(original-a[begin] → max)则会影响 a[maxi] =? max
		if (begin == maxi)//如果原本begin指向的数是max，则swap之后这个数已经被交换到了mini所指向的位置
			maxi = mini;
		Swap(&a[end], &a[maxi]);
		++begin;
		--end;
	}
}

// 堆排序
void AdjustDwon(int* a, int n, int root)
{
	assert(a);
	int parent = root;
	int child = parent * 2 + 1;

	while (child < n)
	{
		if ((child + 1) < n && a[child + 1] > a[child])
			++child;
		if (a[parent] < a[child])
			Swap(&a[parent], &a[child]);
		else
			break;

		parent = child;
		child = parent * 2 + 1;
	}
}
void HeapSort(int* a, int n)
{
	assert(a);

	//建大堆
	for (int parent = (n - 1 - 1) / 2; parent >= 0; parent--)
	{
		AdjustDwon(a, n, parent);
	}

	int end = n - 1;
	while (end)
	{
		Swap(&a[0], &a[end]);
		AdjustDwon(a, end, 0);
		end--;
	}
}
// 冒泡排序
void BubbleSort(int* a, int n)
{
	assert(a);
	for (int j = 0; j < n; j++)
	{
		for (int i = 0; i < n - j - 1; i++)
		{
			if (a[i] > a[i + 1])
				Swap(&a[i], &a[i + 1]);
		}
	}
}

// 快速排序递归实现
// 三数取中
int GetMidIndex(int* a, int left, int right)
{
	int begin = left, end = right;
	int middle = (left + right) / 2;

	if (a[begin] < a[end])
	{
		if (a[middle] < a[begin])
			return begin;
		else if (a[middle] > a[end])
			return end;
		else
			return middle;
	}
	else
	{
		if (a[middle] < a[end])
			return end;
		else if (a[middle] > a[begin])
			return begin;
		else
			return middle;
	}

}
// 快速排序hoare版本
int hoareSort1(int* a, int left, int right)
{
	assert(a);
	if (left >= right)
		return;

	// if ((right - left + 1) < 5)
	// {
	// 	InsertSort(a + left, right - left + 1);
	// }
	else
	{
		int key = left, begin = left, end = right;

		int mid = GetMidIndex(a, left, right);

		Swap(&a[mid], &a[key]);
		while (left < right)
		{
			while (left < right && a[right] >= a[key])
			{
				--right;
			}
			while (left < right && a[left] <= a[key])
			{
				++left;
			}
			Swap(&a[left], &a[right]);
		}
		Swap(&a[key], &a[right]);//left==right

		//[begin,left-1] [right+1,end]
		hoareSort1(a, begin, left - 1);
		hoareSort1(a, right + 1, end);
	}
	return right;
}

// 快速排序挖坑法
int HoleSort2(int* a, int left, int right)
{
	if (left >= right)
		return;
	int key = a[left];
	int hole = left, begin = left, end = right;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			--right;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			++left;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[right] = key;

	//[begin,left-1] [right+1,end]
	HoleSort2(a, begin, left - 1);
	HoleSort2(a, right + 1, end);

	return right;
}

// 快速排序前后指针法
int PointSort3(int* a, int left, int right)
{
	assert(a);
	if (left >= right)
		return;
	int keyi = left;
	int prev = left, cur = left;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && cur != prev)
			Swap(&a[++prev], &a[cur]);

		++cur;
	}
	Swap(&a[keyi], &a[prev]);

	//[left,prev-1][prev+1,right]
	PointSort3(a, left, prev - 1);
	PointSort3(a, prev + 1, right);

	return prev;
}

// 快速排序 非递归实现
void QuickSort(int* a, int left, int right)
{
	assert(a);
	Stack st;
	StackInit(&st);
	StackPush(&st, left);
	StackPush(&st, right);
	while (!StackEmpty(&st))
	{
		int end = StackTop(&st);
		StackPop(&st);
		int begin = StackTop(&st);
		StackPop(&st);
		int keyi = hoareSort1(a, begin, end);

		//[begin,keyi-1] keyi [keyi+1,end]
		if (keyi + 1 < end)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, end);
		}
		if (begin < keyi - 1)
		{
			StackPush(&st, begin);
			StackPush(&st, keyi - 1);
		}
	}

	StackDestroy(&st);
}
// 归并排序递归实现
void _MergeSort(int* a, int left, int right, int* tmp)
{
	assert(a && tmp);

	if (left == right)
		return;

	int middle = (left + right) / 2;
	//[left,  middle] [middle+1,right]
	//[begin1,end1]   [begin2,end2]
	int begin1 = left, end1 = middle, begin2 = middle + 1, end2 = right;

	//递归分解
	_MergeSort(a, begin1, end1, tmp);
	_MergeSort(a, begin2, end2, tmp);

	//merge
	int i = begin1;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* a, int n)
{
	assert(a);
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (!tmp)
	{
		perror("malloc fail");
		exit(-1);
	}

	_MergeSort(a, 0, n - 1, tmp);

    free(tmp);
    tmp = NULL;
}

// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
	assert(a);
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (!tmp)
	{
		perror("malloc fail");
		exit(-1);
	}

	int range = 1;
	while (range < n)
	{
		for (int i = 0; i < n; i += 2 * range)
		{
			int begin1 = i, end1 = i + range - 1;
			int begin2 = i + range, end2 = i + 2 * range - 1;
			int j = begin1;

			//越界
			//end1越界
			if (end1 >= n)
			{
				end1 = n - 1;
				begin2 = end2 + 1;//begin2 > end2;
			}
			else if (begin2 == n)
			{
				begin2 = end2 + 1;//begin2 > end2;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}
			//merge
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

		}
		memcpy(a, tmp, sizeof(int)*n);

		range *= 2;
	}

	free(tmp);
	tmp = NULL;
}

// 计数排序
void CountSort(int* a, int n)
{
	assert(a);
	int min = a[0], max = a[0];
	for (size_t i = 0; i < n; i++)
	{
		if (a[i] > max)
			max = a[i];
		if (a[i] < min)
			min = a[i];
	}
	int size = max - min + 1;
	int* tmp = (int*)calloc(size, sizeof(int));
	if (!tmp)
	{
		perror("calloc fail");
		exit(-1);
	}

	//计数
	for (size_t i = 0; i < n; i++)
	{
		++tmp[*(a + i) - min];
	}
	int j = 0;
	for (size_t i = 0; i < size; i++)
	{
		while (tmp[i]--)
		{
			a[j++] = i + min;
		}
	}
    free(tmp);
    tmp = NULL;
}

int* sortArray(int* nums, int numsSize, int* returnSize){
   *returnSize=numsSize;
    //InsertSort(nums,numsSize);//超出时间限制
    //ShellSort(nums,numsSize);

    //SelectSort(nums,numsSize);//超出时间限制
    //HeapSort(nums,numsSize);

    //BubbleSort(nums,numsSize);//超出时间限制
    //hoareSort1(nums,0,numsSize-1);//对于大量重复数据，超出时间限制
    //HoleSort2(nums,0,numsSize-1);//超出时间限制
    //PointSort3(nums,0,numsSize-1);//对于大量有序数据，超出时间限制
    //QuickSort(nums,0,numsSize-1);//对于大量重复数据，超出时间限制

    //MergeSort(nums,numsSize);
    //MergeSortNonR(nums,numsSize);

    //CountSort(nums,numsSize);
    return nums;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/434716.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【数据结构】队列（循环队列和链队列）详细讲解各种操作

【数据结构】队列（循环队列和链队列）详细讲解各种操作

&#x1f38a;专栏【数据结构】 &#x1f354;喜欢的诗句&#xff1a;更喜岷山千里雪 三军过后尽开颜。 &#x1f386;音乐分享【勋章】 大一同学小吉&#xff0c;欢迎并且感谢大家指出我的问题&#x1f970; 图片来源网络&#xff0c;如果侵权&#xff0c;请联系我 目录 ⭐队…
阅读更多...
爱智EdgerOS之深入解析离线下载任务

爱智EdgerOS之深入解析离线下载任务

一、需求分析 在日常使用计算机的过程中&#xff0c;看到喜欢的资源不可避免地想把它下载到我们的设备上保存下来&#xff0c;比如图片&#xff0c;音视频资源&#xff0c;文档资源等&#xff0c;基于这种应用场景&#xff0c;现在来看看在爱智设备上可以如何实现呢&#xff1…
阅读更多...
日撸 Java 三百行day33

日撸 Java 三百行day33

文章目录 说明day33 图的广度优先遍历1.思路2.多个连通分量2 代码实现 说明 闵老师的文章链接&#xff1a; 日撸 Java 三百行&#xff08;总述&#xff09;_minfanphd的博客-CSDN博客 自己也把手敲的代码放在了github上维护&#xff1a;https://github.com/fulisha-ok/sampled…
阅读更多...
82.qt qml-2D粒子系统、粒子方向、粒子项（一）

82.qt qml-2D粒子系统、粒子方向、粒子项（一）

由于粒子系统相关的类比较多, 所以本章参考自QmlBook in chinese的粒子章节配合学习: 由于QmlBook in chinese翻译过来的文字有些比较难理解,所以本章在它的基础上做些个人理解,建议学习的小伙伴最好配合QmlBook in chinese一起学习。 1.介绍 粒子模拟的核心是粒子系统(Partic…
阅读更多...
ResNet残差网络

ResNet残差网络

ResNet 目的 Resnet网络是为了解决深度网络中的退化问题&#xff0c;即网络层数越深时&#xff0c;在数据集上表现的性能却越差。 原理 ResNet的单元结构如下&#xff1a; 类似动态规划的选择性继承&#xff0c;同时会在训练过程中逐渐增大&#xff08;/缩小&#xff09;该…
阅读更多...
数字图像基础【7】应用线性回归最小二乘法(矩阵版本)求解几何变换(仿射、透视)

数字图像基础【7】应用线性回归最小二乘法(矩阵版本)求解几何变换(仿射、透视)

这一章主要讲图像几何变换模型&#xff0c;可能很多同学会想几何变换还不简单嚒&#xff1f;平移缩放旋转。在传统的或者说在同一维度上的基础变换确实是这三个&#xff0c;但是今天学习的是2d图像转投到3d拼接的基础变换过程。总共包含五个变换——平移、刚性、相似、仿射、透…
阅读更多...
尚融宝10-Excel数据批量导入

尚融宝10-Excel数据批量导入

目录 一、数据字典 &#xff08;一&#xff09;、什么是数据字典 &#xff08;二&#xff09;、数据字典的设计 二、Excel数据批量导入 &#xff08;一&#xff09;后端接口 1、添加依赖 2、创建Excel实体类 3、创建监听器 4、Mapper层批量插入 5、Service层创建监听…
阅读更多...
2023年，想要靠做软件测试获得高薪，我还有机会吗？

2023年，想要靠做软件测试获得高薪，我还有机会吗？

时间过得很快&#xff0c;一眨眼&#xff0c;马上就要进入2023年了&#xff0c;到了年底&#xff0c;最近后台不免又出现了经常被同学问道这几个问题&#xff1a;2023年还能转行软件测试吗&#xff1f;零基础转行可行吗&#xff1f; 本期小编就“2023年&#xff0c;入行软件测…
阅读更多...
一文解决nltk安装问题ModuleNotFoundError: No module named ‘nltk‘，保姆级教程

一文解决nltk安装问题ModuleNotFoundError: No module named ‘nltk‘，保姆级教程

目录 问题一&#xff1a;No module named ‘nltk‘ 问题二&#xff1a;Please use the NLTK Downloader to obtain the resource 下载科学上网工具 问题三&#xff1a;套娃报错 如果会科学上网&#xff0c;可以直接看问题三 问题一&#xff1a;No module named ‘nltk‘ Mo…
阅读更多...
【微服务笔记16】微服务组件之Gateway服务网关基础环境搭建

【微服务笔记16】微服务组件之Gateway服务网关基础环境搭建

这篇文章&#xff0c;主要介绍微服务组件之Gateway服务网关基础环境搭建。 目录 一、Gateway服务网关 1.1、什么是Gateway 1.2、Gateway基础环境搭建 &#xff08;1&#xff09;基础环境介绍 &#xff08;2&#xff09;引入依赖 &#xff08;3&#xff09;添加路由配置信…
阅读更多...
软件测试工程师的进阶之旅

软件测试工程师的进阶之旅

很多人对测试工程师都有一些刻板印象&#xff0c;比如觉得测试“入门门槛低&#xff0c;没有技术含量”、“对公司不重要”、“操作简单工作枯燥”“一百个开发&#xff0c;一个测试”等等。 会产生这种负面评论&#xff0c;是因为很多人对测试的了解&#xff0c;还停留在几年…
阅读更多...
Lesson12 udptcp协议

Lesson12 udptcp协议

netstat命令->查看网络状态 n 拒绝显示别名&#xff0c;能显示数字的全部转化成数字l 仅列出有在 Listen (监听) 的服務状态p 显示建立相关链接的程序名t (tcp)仅显示tcp相关选项u (udp)仅显示udp相关选项a (all)显示所有选项&#xff0c;默认不显示LISTEN相关 pidof命令-&…
阅读更多...
SQL select详解（基于选课系统）

SQL select详解（基于选课系统）

表详情&#xff1a; 学生表&#xff1a; 学院表&#xff1a; 学生选课记录表&#xff1a; 课程表&#xff1a; 教师表&#xff1a; 查询&#xff1a; 1. 查全表 -- 01. 查询所有学生的所有信息 -- 方法一&#xff1a;会更复杂&#xff0c;进行了两次查询&#xff0c;第一…
阅读更多...
机器学习笔记之正则化(六)批标准化(BatchNormalization)

机器学习笔记之正则化(六)批标准化(BatchNormalization)

机器学习笔记之正则化——批标准化[Batch Normalization] 引言引子&#xff1a;梯度消失梯度消失的处理方式批标准化 ( Batch Normalization ) (\text{Batch Normalization}) (Batch Normalization)场景构建梯度信息比例不平衡批标准化对于梯度比例不平衡的处理方式 ICS \text{…
阅读更多...
《抄送列表》：过滤次要文件，优先处理重要文件

《抄送列表》：过滤次要文件，优先处理重要文件

目录 一、题目 二、思路 1、查找字符/字符串方法&#xff1a;str1.indexOf( ) 2、字符串截取方法&#xff1a;str1.substring( ) 三、代码 详细注释版&#xff1a; 简化注释版&#xff1a; 一、题目 题目&#xff1a;抄送列表 题目链接&#xff1a;抄送列表 …
阅读更多...
Java[集合] Map 和 Set

Java[集合] Map 和 Set

哈喽&#xff0c;大家好~ 我是保护小周ღ&#xff0c;本期为大家带来的是 Java Map 和 Set 集合详细介绍了两个集合的概念及其常用方法&#xff0c;感兴趣的朋友可以来学习一下。更多精彩敬请期待&#xff1a;保护小周ღ *★,*:.☆(&#xffe3;▽&#xffe3;)/$:*.★* ‘ 一、…
阅读更多...
JVM知识汇总

JVM知识汇总

1、JVM架构图 2、Java编译器 Java编译器做的事情很简单&#xff0c;其实就是就是将Java的源文件转换为字节码文件。 1. 源文件存储的是高级语言的命令&#xff0c;JVM只认识"机器码"&#xff1b; 2. 因此将源文件转换为字节码文件&#xff0c;即是JVM看得懂的"…
阅读更多...
Node.js—Buffer（缓冲器）

Node.js—Buffer（缓冲器）

文章目录 1、概念2.、特点3、创建Buffer3.1 Buffer.alloc3.2 Buffer.allocUnsafe3.3 Buffer.from 4、操作Buffer4.1 Buffer 与字符串的转化4.2 Buffer 的读写 参考 1、概念 Buffer 是一个类似于数组的对象 &#xff0c;用于表示固定长度的字节序列。Buffer 本质是一段内存空间…
阅读更多...
视觉学习(四) --- 基于yolov5进行数据集制作和模型训练

视觉学习(四) --- 基于yolov5进行数据集制作和模型训练

环境信息 Jetson Xavier NX&#xff1a;Jetpack 4.4.1 Ubuntu&#xff1a;18.04 CUDA: 10.2.89 OpenCV: 4.5.1 cuDNN&#xff1a;8.0.0.180一.yolov5 项目代码整体架构介绍 1. yolov5官网下载地址&#xff1a; GitHub: https://github.com/ultralytics/yolov5/tree/v5.0 2. …
阅读更多...
单元测试中的独立运行

单元测试中的独立运行

单元测试中的独立运行 单元测试是针对代码单元的独立测试。要测试代码单元&#xff0c;首先要其使能够独立运行。项目中的代码具有依赖关系&#xff0c;例如&#xff0c;一个源文件可能直接或间接包含大量头文件&#xff0c;并调用众多其他源文件的代码&#xff0c;抽取其中的一…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023