这一章主要讲图像几何变换模型，可能很多同学会想几何变换还不简单嚒？平移缩放旋转。在传统的或者说在同一维度上的基础变换确实是这三个，但是今天学习的是2d图像转投到3d拼接的基础变换过程。总共包含五个变换——平移、刚性、相似、仿射、透视

平移、刚性、相似

我们先看最简单的几何变换模型——平移和刚性。首先是平移变换，就一组参数 tx 和 ty组成的一个向量。这个跟我们之前学习OpenGL的时候是一致的，这里就不多说了。然后就是刚性变换，刚性变换在平移变换的基础上，增加旋转角度θ相关的矩阵。刚性变换的一个特点，就是不改变图像内部结构的长度和角度。

那么旋转矩阵的它是怎么来的，我们可以利用变换前后的两组点位置，用数学关系推导。两坐标点通过圆半径等长作为中间恒量，就可以写出数学恒等式。然后会发现，旋转矩阵是一个很完美的矩阵，它是一个正交矩阵。

• 正交矩阵的行列式为1
• 且每个列向量都是单位向量且相互正交
• 它的逆等于它的转置 R(-1)是R(T)

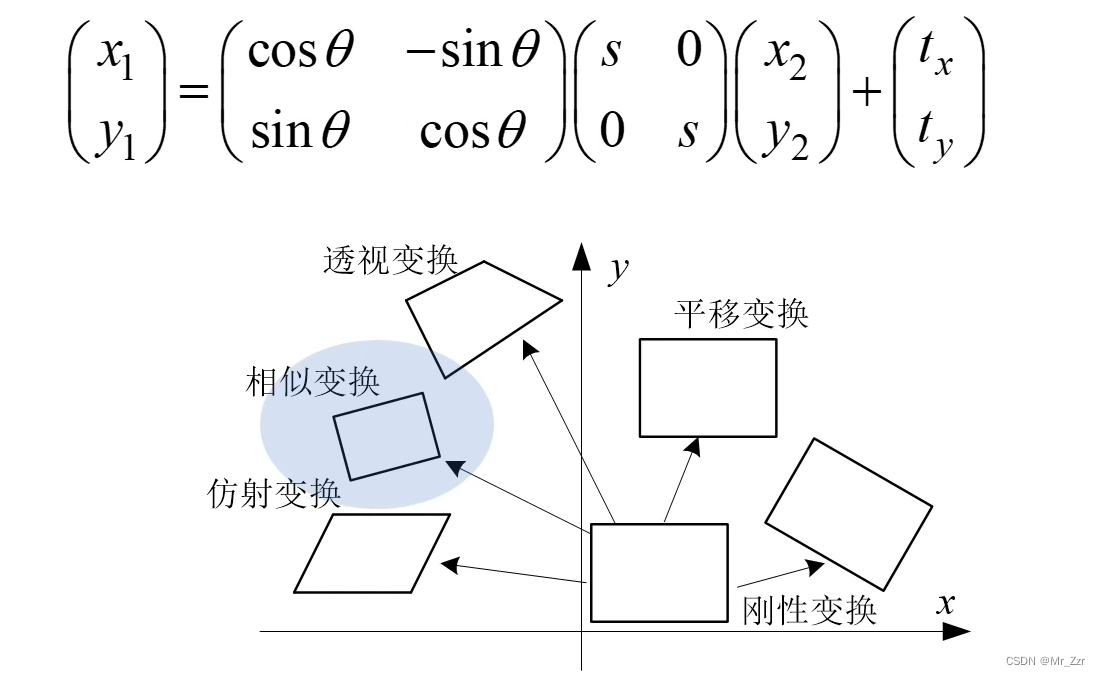
接着我们再说第三个变换，相似变换。这个变换又是在前者（刚性变换）的基础上增加了缩放尺度的矩阵。因为存在缩放，所以相似变换它会改变目标内部结构的长度，但还是保持着对象内部角度的不变性。这些都在OpenGL的时候接触过，数学原理就不在这展开了。（建议同学可以在平时吃午饭的时候回顾一下线性代数，推荐B站的这套教学视频）

仿射、透视

接下来说说本篇的重点，仿射变换和透视变换。两者在机器视觉里面是很重要的变换，无论是在二维的图像处理和三维的网格处理当中都经常使用到。

我们先看仿射变换，它由一个线性变换矩阵+平移向量组成。线性变换矩阵T=[a, b, c, d]四个参数来表示。上图很清楚的表达了仿射变换前后带来的变形，其对象内部结构也会发生变换，但是其内部结构的平行性是可以得到保持的。下面我们来看一个仿射变换的例子。

当设置单位矩阵(a、d = 1.0)的时候，是一个有缩放能力的单位阵，图形对象保持原样没有变形；把参数b=0.2以后，原来的正方形的两边发生了倾斜变形；把参数c=0.2以后，原来的正方形的上下底边发生了旋转进而使得正方形也发生了变形；所以仿射变换它不仅会带来旋转而且还会变形，但图像内的平行性是相对不变的，是一个相对自由的线性变换。

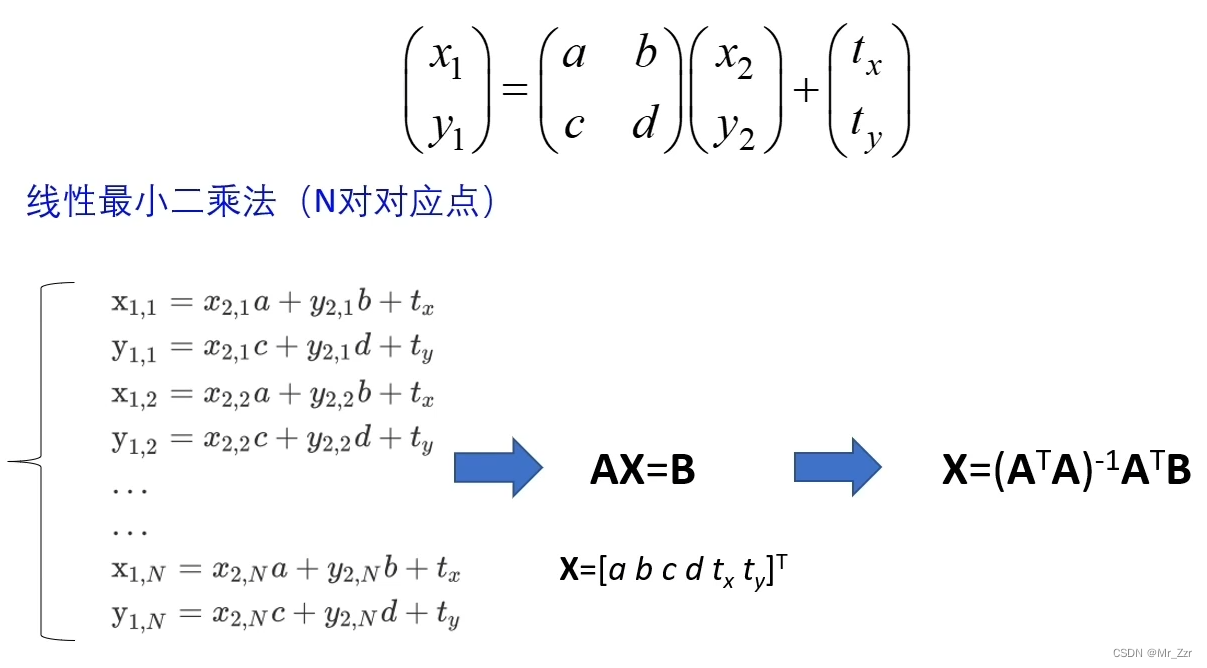
有了概念之后，那么是如何求 仿射变换的矩阵系数呢？细想后发现，我们可以把仿射变换的矩阵看成K，那么仿射变换是不是就变成了小时候学习的二元一次方程 Y=KX+B ？此时就需要N组变换点，注意上图给的例子，(x1.1，y1.1) 和 (x2.1，y2.1)对应，表示第一组变换点。(x1.2，y1.2) 和 (x2.2，y2.2)对应，表示第二组变换点，如此类推到第N组变换点，各自都写成了矩阵乘法的代数式，总共有2N个代数式。

由线性回归的思想，在用最小二乘法就可以推导出X的公式，代入就可以求出其矩阵的具体参数。

紧接着我们看最后一个变换——透视变换（也叫投影变换）我们在说仿射变换的时候呢，它保持着图形对象内部结构的不变性。在透视变换中，图形对象内部结构的平行性也不能保持不变了，它是一个更加灵活自由度最大的一个变换模型。

从参数矩阵分析，此模型变换共有8个可变参数(也叫8个自由度)，有两种表达形式数学代数形式 和 矩阵形式。当写成矩阵形式的时候，这个矩阵名称叫 H 单应矩阵(Homography)。这个透视变换它是计算机世界里面一个很重要的模型，比如说我们用一个针孔相机去拍一个平面，那么平面上的目标和我们图像上的目标会有一个对应关系，这个关系就可以用这个单应矩阵来表达（假设这个相机不存在畸变）

这里給出一个例子，介绍如何求解透视变换的单应矩阵。我们可以把输入输出写成特征矩阵的形式，仍然是一对点，2组方程，就可以利用线性回归的最小二乘法求解得到其单应矩阵参数。

线性回归——最小二乘法（矩阵版本）

那么对应到矩阵的二元一次方程该是如何计算呢？有请主角——矩阵版本的“最小二乘法”。

先看看百度百科是如何描述的：最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合，其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

这里我尝试用最简单直白的语言描述一下矩阵版本的最小二乘法的核心思想。与其说最小二乘法是一个数学方法，我觉得它是由离散(特征)点去推导线性关系的一种解题细想。如果输入输出确定存在某种大致的线性关系，那么用真实的 Y' 值，减去 KX（K未知）其差值应该为0，或者其差值为恒定值B。注意这里的 “真实的 Y' 值”，并不是上面二元一次方程 Y=KX+B的Y，这里一定要区分开。那么这里就可以引申出机器学习中的损失函数的概念：

SSELoss(k) = || Y' - KX ||²

那么我们只需要把SSELoss损失函数的值控制在最小，也或者是说对SSELoss求导后，令其为0（函数斜率恒定，不在有变化）那么就可以得到我们的所希望的线性关系的参数代数式。

原理思想就是这个，那么我们这里开始深入分析最小二乘法，并尝试以矩阵形式进行展开。

第一步，列举一个多元线性方程的通用公式 f(x) = w₁x₁ + w₂x₂ ... wnxn + b， 这里的共n个自变量（x₁、x₂一直到xn）和n个特征（w₁、w₂一直到wn），常数b表示截距的意思。

第二步，改写矩阵相乘的形式，把特征提取成一个特征矩阵w = [w₁,w₂, ... wn]┬，自变量x = [x₁,x₂, ... xn]┬（┬代表矩阵的转置）那么第一步的通用公式就可以写成 f(x) = w┬·x + b（加粗效果w和x代表矩阵）

第三步，把多组自变量数据(假设共有m组测试数据)，每一组改写成自变量矩阵x的形式。这样左边就能组成一个m行，n+1列的输入矩阵。右边就是对应的因变量构成m行1列的结果矩阵。这样 f(x) = w┬·x + b就具体形象起来了。

第四步，我们考虑把截距b也纳入进特征矩阵，另其也当成一个恒定的特征量。新定义w-hat = [w₁,w₂, ... wn, b]┬，相对应的x-hat = [x₁,x₂, ... xn, 1]┬，并定义由所有测试数据集所组成的矩阵 X-hat 。这样原来的f(x) = w┬·x + b，就可以改写成 f(x) = w-hat┬ · x-hat。而对应具体的测试数据集和结果集就可以写成 y =​​​​​​​ ​​​​​​​X-hat · w-hat（注意矩阵乘法顺序、转置不能搞错）

第五步，构造损失函数SSELoss(w)，我们用真实结果集 y 减去 X-hat·w-hat，再求2-范式。根据2-范式的定义，我们可以巧妙的把损失函数-代数2-范式的形式，改写成矩阵相乘的写法。（可以仔细想想 1xN的矩阵 和 Nx1的矩阵相乘后的代数式展开）

第六步，也是最后一步，就和开始前介绍思想原理的时候说的，对损失函数SSELoss(w)求导，并求解其导函数为0的时候，特征矩阵w的表达形式。

详情请参考B站这套课程。Lesson 2.2 机器学习矩阵求导与最小二乘法_哔哩哔哩_bilibili

That ‘ s All.