用二叉树或栈求表达式的值--代码实现+算法分析

news2024/11/24 17:29:28

解决表达式求值问题有两种方法，一种是利用栈和后缀表达式求解，另一种是二叉树中序存储表达式。所以本文分为栈和二叉树两大部分带领读者求解表达式。

1. 利用栈解决表达式求值问题

所谓表达式，就是由变量、常量以及运算符组合而成的式子。其中，常用的运算符无非 !（阶乘运算符）、^（指数 运算符）、+、-、*、/ 、( ) 这几种，比如 3!+4*2/(1-5)^2 就是一个表达式。 那么，如何用求一个表达式的值呢。用后缀表达式法。

什么是后缀表达式？就是将表达式中所有运算符放在它的运算项后面

这里以 3!+4*2/(1-5)^2 为例：6+8/16

  • ! 运算符对应的运算项为 3，转换后得到3!
  • +运算符对应的运算项是 3! 和 4*2/(1-5)^2，转换之后得到：3! 4*2/(1-5)^2 +
  • *运算符对应的运算项是 4 和 2，转换之后得到 4 2 *
  • / 运算符对应的运算项是4 2 *和(1-5)^2，转换后得到 4 2 * (1-5)^2 /
  • -运算符对应的运算项是 1 和 5，转换后得到1 5 -
  • ^运算符对应的运算项是1 5 -和2，转换后得到 1 5 - 2 ^。

整合之后，整个普通表达式就转换成了 3 ! 4 2 * 1 5 - 2 ^ / +这就是其对应的后缀表达式。

得到的后缀表达式，如何计算？首先创建一个栈。接着按照从左到右的顺序扫描后缀表达式，遇到运算项就入栈。遇到n元运算符，就出栈顶元素n个计算并将计算结果压回栈中。代码实现应注意的是：从栈出来的先后顺序，对应原来运算的哪一个运算项！

如：遇到阶乘（一元运算符），出栈顶计算。遇到乘法（二元运算符），出栈顶两元素计算并压回栈中。循环上述操作，最后栈中最后一个元素，即为此运算项即为整个表达式的值。

  • 根据后缀表达式求值代码实现
double calculate(char* out)
{
	int index = 0;
	stack<double>result;
	while (out[index] != '\0')
	{
		char c = out[index];
		switch (c)
		{
			case '!':
			{
				double i = result.top();
				result.pop();
				double end = 1;
				while (i != 1) end *= i-- ;
				result.push(end);
				break;
			}
			case '*':
			{
				double right = result.top();
				result.pop();
				double left = result.top();
				result.pop();
				result.push(left * right);
				break;
			}
			case '/':
			{
				double right = result.top();//被除数
				result.pop();
				double left = result.top();//除数
				result.pop();
				if (!right)
				{
					cout << "分母为零，错误" << endl;
					exit(-1);
				}
				else
				{
					result.push(left / right);
					break;
				}
			}
			case '+':
			{
				double right = result.top();
				result.pop();
				double left = result.top();
				result.pop();
				result.push(left + right);
				break;
			}
			case '-':
			{
				double right = result.top();//被减数
				result.pop();
				double left = result.top();//减数
				result.pop();
				result.push(left - right);
				break;
			}
			case '^':
			{
				double exp = result.top();//指数
				result.pop();
				double base = result.top();//底数
				result.pop();
				if (!base)
				{
					cout << "底数为零" << endl;
					exit(-1);
				}
				else
				{
					double end = 1;
					for (int i = 0; i < exp; i++)
					{
						end *= base;
					}
					result.push(end);
					break;
				}
			}
			default:
			{
				result.push(c - 48);
			}
		}
		index++;
	}
	return result.top();

}

1.2 根据表达式求后缀表达式

表达式求值的核心就是将波兰式（一般常见的表达式）转化为逆波兰式（后缀表达式）。上面讲过了如何根据后缀表达式求解表达式的值，那么如何获得后缀表达式？可以用二叉树，也可以用栈，这里讲解用栈的方式。

首先看规则：

普通表达式转换为后缀表达式需要用到一个空栈（假设名为Optr）和一个空数组（数组名）

  • 如果为 ‘0’~‘9’ 的字符，将其添加到 postexp 数组的末尾；
  • 如果该字符为除 ‘(’ 和 ‘)’ 以外的运算符，将其与 Optr 栈顶的运算符进行优先级比较（如乘法高于加法），如果该运算符优先级高于或等于栈顶运算符，则将其入栈；反之，如果该运算符优先级小于或等于栈顶运算符，则将栈顶运算符出栈并添加到 postexp 数组的尾部，然后继续拿当前运算符同新的栈顶运算符做大小比较，以此类推。
  • 如果该字符为 ‘(’ 运算符，直接入栈；如果为 ‘)’ 运算符，依次取 Optr 栈顶运算符并将其添加到 postexp 数组末尾，直到遇到 ‘(’ 字符为止（注意，‘(’ 字符也从栈顶取出，但不将其添加 postexp 数组中）。

依照以上处理过程，直到将普通表达式遍历完毕，如果 Optr 栈中仍有运算符，依次将它们出栈并添加到 postex数组尾部。最终，postexp 数组内存储的表达式就是转换后的后缀表达式。

总结一句：运算项直接放数组中，运算符压入栈中，只有遇到比栈顶运算符优先级低的或栈空才出栈放入数组中。括号单独考虑。

如此一来运算符优先级高的就紧随运算项，先运算。运算符优先级低的往往在后缀表达式最右边。

下面是表达式3 ! 4 2 * 1 5 - 2 ^ / +转换为后缀表达式的过程：（按序号看）

image-20221029002310515

代码实现

void transform(char* expr, char* out)
{
	stack<char>temp;
	int index = 0;//作为输出数组的下标
	int i = 0;//表达式的下标
	while(expr[i]!='\0')
	{
		char c = expr[i];
		switch (c)
		{
			case '!':
			{
				while (!temp.empty()) 
				{
					if (temp.top() == '!')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('!');
				i++;
				break;
			}case '*':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' || temp.top() == '/')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('*');
				i++;
				break;
			}case '/':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' || temp.top() == '/')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('/');
				i++;
				break;
			}case '+':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' 
						|| temp.top() == '/' || temp.top() == '+' || temp.top() == '-')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('+');
				i++;
				break;
			}case '-':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*'
						|| temp.top() == '/' || temp.top() == '+' || temp.top() == '-')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('-');
				i++;
				break;
			}case '(':
			{
				temp.push('(');
				i++;
				break;
			}case ')':
			{
				while (temp.top() != '(')
				{
					char ch = temp.top();
					temp.pop();
					out[index++] = ch;
				}
				temp.pop();//此时栈顶为（
				i++;
				break;
			}case '^':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!'||temp.top()=='^')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('^');
				i++;
				break;
			}default :
			{
				out[index++] = c;
				i++;
				break;
			}
		
		}
	}
	//此时将栈中多有的数据逐一出栈
	while (!temp.empty())
	{
		out[index++] = temp.top();
		temp.pop();
	}
	out[index] = '\0';//最后给后缀表达式加上尾\0
}
int main() {
	char* s = (char*)malloc(15 * sizeof(char));
	char* out = (char*)malloc(13 * sizeof(char));
	char temp[] = "3!+4*2/(1-5)^2";
	//cout << strlen(s);
	for (int i = 0; i < 15; i++)
	{
		s[i] = temp[i];
	}
	transform(s,out);
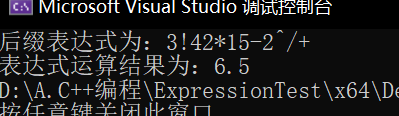
	cout << "后缀表达式为："<< out << endl;
	cout <<"表达式运算结果为："<< calculate(out);

}
image-20221029141426025

2. 二叉树求表达式值

2.1 二叉树存储表达式

表达式转换成二叉树的思路和栈其实类似，下面是具体算法思路

【算法步骤】

  1. 初始化OPTR栈和EXPT栈

  2. 按序逐个读取表达式字符。则循环执行以下操作。

    • 若ch不是运算符，则以ch为根创建一棵只有根节点的二叉树，且将该树根节点压入EXPT栈。

    • 若ch是运算符。若栈为空直接入栈，不用处理。若栈非空，则将ch运算符和根据OPTR的栈顶元素优先级比较结果，进行不同的处理；

      若ch优先级大于栈顶，则将ch压入OPTR栈

      若ch优先级小于或等于栈顶，则弹出OPTR栈顶的运算符，从EXPT栈弹出两个表达式子树的根节点。运算符为根节点，以EXPT栈中弹出的第二个子树作为左子树，以EXPT栈中弹出的第第一个子树作为右子树，创建一棵新二叉树并将该树根节点压入EXPT栈，成为新的表达式子树

此处的代码只考虑了±*/（），代码包括按序取字符，针对不同字符用switch语句处理，代码量主要就是在switch语句这里

#include<iostream>
#include<stack>
using namespace std;

typedef char BTDataType;
struct BTNode {
	BTDataType data;
	BTNode* left;
	BTNode* right;
};

BTNode* newNode(BTDataType data) {
	BTNode* root = new BTNode;
	root->data = data;
	root->left = NULL;
	root->right = NULL;
	return root;
}
//将表达式换成对应的二叉树
BTNode* transform(string exp) {
	stack<char>OPTR;//运算符栈
	stack<BTNode*>EXPT;//表达式栈

	for (int i = 0; i < exp.size(); i++) {
		if (exp[i] >= 48 && exp[i] <= 57) {
			BTNode* root = newNode(exp[i]);
			EXPT.push(root);
		}
		else {
			if (OPTR.empty()||exp[i]=='(')OPTR.push(exp[i]);
			else {
				//考虑到的运算有：+-*/()
				switch (exp[i]) {
					case '*': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '+' || top == '-' || top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环在循环外统一入栈
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;
								
								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('*');
						break;
					}
					case '/': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '+' || top == '-' || top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('/');
						break;
					}
					case '-': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								OPTR.push('-');
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('-');
						break;
					}
					case '+': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('+');
						break;
					}
					case '(': {
						OPTR.push('(');
						break;
					}
					case ')': {
						while (OPTR.top()!='(') {
							//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
							char top = OPTR.top();
							BTNode* root = newNode(top);
							OPTR.pop();

							//取得前两个表达式
							BTNode* exp1 = EXPT.top();
							EXPT.pop();
							BTNode* exp2 = EXPT.top();
							EXPT.pop();

							//左右子树链接
							root->left = exp2;
							root->right = exp1;

							//表达式压回栈
							EXPT.push(root);
						}
						OPTR.pop();//将（出栈
						break;
					}
				}
			}
		}
	}
	//此时将OPTR栈中所有的元素出栈，换称对应的表达式到EXPT中
	while (!OPTR.empty()) {
		//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
		char top = OPTR.top();
		BTNode* root = newNode(top);
		OPTR.pop();

		//取得前两个表达式
		BTNode* exp1 = EXPT.top();
		EXPT.pop();
		BTNode* exp2 = EXPT.top();
		EXPT.pop();

		//左右子树链接
		root->left = exp2;
		root->right = exp1;

		//表达式压回栈
		EXPT.push(root);
	}
	return EXPT.top();
}

2.2 用二叉树求表达式的值

表达式树的求值【算法步骤】

  1. 设变量lvalue和rvalue分别用以记录表达式树中左子树和右子树的值,初始均为0。
  2. 如果当前节点为叶子（节点为操作数），则返回该节点的数值,否则(节点为运算符）执行以下操作:
    递归计算左子树的值，记为Ivalue;递归计算右子树的值,记为rvalue;
    根据当前节点运算符的类型，将lvalue和rvalue进行相应运算并返回。

代码实现：

double valueBTree(BTNode* root)
{
	if (root->data >= 48 && root->data <= 57)return root->data-48;
	else {
		double lvalue = valueBTree(root->left);
		double rvalue = valueBTree(root->right);
		switch (root->data) {
			case '+': {
				return lvalue + rvalue;
				break;
			}
			case '-': {
				return lvalue - rvalue;
				break;
			}
			case '*': {
				return lvalue * rvalue;
				break;
			}
			case '/': {
				return lvalue / rvalue;
				break;
			}
		}
	}
}

2.3 二叉树求表达式完整测试代码

#include<iostream>
#include<stack>
using namespace std;

typedef char BTDataType;
struct BTNode {
	BTDataType data;
	BTNode* left;
	BTNode* right;
};

BTNode* newNode(BTDataType data) {
	BTNode* root = new BTNode;
	root->data = data;
	root->left = NULL;
	root->right = NULL;
	return root;
}
//将表达式换成对应的二叉树
BTNode* transform(string exp) {
	stack<char>OPTR;//运算符栈
	stack<BTNode*>EXPT;//表达式栈

	for (int i = 0; i < exp.size(); i++) {
		if (exp[i] >= 48 && exp[i] <= 57) {
			BTNode* root = newNode(exp[i]);
			EXPT.push(root);
		}
		else {
			if (OPTR.empty()||exp[i]=='(')OPTR.push(exp[i]);
			else {
				//考虑到的运算有：+-*/()
				switch (exp[i]) {
					case '*': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '+' || top == '-' || top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环在循环外统一入栈
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;
								
								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('*');
						break;
					}
					case '/': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '+' || top == '-' || top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('/');
						break;
					}
					case '-': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								OPTR.push('-');
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('-');
						break;
					}
					case '+': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('+');
						break;
					}
					case '(': {
						OPTR.push('(');
						break;
					}
					case ')': {
						while (OPTR.top()!='(') {
							//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
							char top = OPTR.top();
							BTNode* root = newNode(top);
							OPTR.pop();

							//取得前两个表达式
							BTNode* exp1 = EXPT.top();
							EXPT.pop();
							BTNode* exp2 = EXPT.top();
							EXPT.pop();

							//左右子树链接
							root->left = exp2;
							root->right = exp1;

							//表达式压回栈
							EXPT.push(root);
						}
						OPTR.pop();//将（出栈
						break;
					}
				}
			}
		}
	}
	//此时将OPTR栈中所有的元素出栈，换称对应的表达式到EXPT中
	while (!OPTR.empty()) {
		//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
		char top = OPTR.top();
		BTNode* root = newNode(top);
		OPTR.pop();

		//取得前两个表达式
		BTNode* exp1 = EXPT.top();
		EXPT.pop();
		BTNode* exp2 = EXPT.top();
		EXPT.pop();

		//左右子树链接
		root->left = exp2;
		root->right = exp1;

		//表达式压回栈
		EXPT.push(root);
	}
	return EXPT.top();
}

double valueBTree(BTNode* root)
{
	if (root->data >= 48 && root->data <= 57)return root->data-48;
	else {
		double lvalue = valueBTree(root->left);
		double rvalue = valueBTree(root->right);
		switch (root->data) {
			case '+': {
				return lvalue + rvalue;
				break;
			}
			case '-': {
				return lvalue - rvalue;
				break;
			}
			case '*': {
				return lvalue * rvalue;
				break;
			}
			case '/': {
				return lvalue / rvalue;
				break;
			}
		}
	}
}
int main() {
	string sample = "(1+2)*3-4/5";
	BTNode* root =transform(sample);
	cout << endl;
	cout << "输入：" << sample << endl;
	cout << "输出" << valueBTree(root) << endl;

	sample = "1+2*3-4/5";
	root = transform(sample);
	cout << endl;
	cout << "输入：" << sample << endl;
	cout << "输出" << valueBTree(root) << endl;
}

image-20221128172659999

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/43201.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

集群部署看过来，低代码@AWS智能集群的架构与搭建方案

集群部署看过来，低代码@AWS智能集群的架构与搭建方案

亚马逊AWS是葡萄城的生态合作伙伴。为了帮助您充分利用AWS的托管服务快速构建起一套集群环境&#xff0c;彻底去掉“单一故障点”&#xff0c;实现最高的可用性&#xff0c;我们准备了**《低代码智能集群AWS的架构与搭建方案》**看完本文&#xff0c;带你掌握“基于nginx配置服…
阅读更多...
Origin绘制多折线图

Origin绘制多折线图

Origin的优势区间相对于python和R在于数据量大时处理方便 尤其是多维度、多线、多拟合 尝试复现上图 1.首先把20列数据复制过去 2.全选之后&#xff08;ctrlA&#xff09;&#xff0c;然后点Plot——Line 3.随便选一根线&#xff0c;双击进入属性设置&#xff08;Origin交互设…
阅读更多...
计算机网络-传输层：TCP协议

计算机网络-传输层：TCP协议

目录 一、协议格式 二、协议特性 1.面向连接 1.1三次握手建立连接 1.2四次挥手断开连接 为什么握手是三次&#xff0c;挥手是四次&#xff1f; 三次握手失败后&#xff0c;两端如何处理&#xff1f; 一台主机上出现了大量CLOSE_WAIT状态连接的原因&#xff1f; TIME_W…
阅读更多...
基于神经网络多项式插值的图像超分辨重构研究-附Matlab代码

基于神经网络多项式插值的图像超分辨重构研究-附Matlab代码

⭕⭕ 目 录 ⭕⭕✳️ 一、引言✳️ 二、基于单帧图像的超分辨率重构技术✳️ 2.1 最近邻域插值法✳️ 2.2 双线性插值法✳️ 2.3 双三次插值法(Keys’插值)✳️ 三、神经网络插值原理✳️ 3.1 训练阶段&#xff1a;✳️ 3.2 测试阶段✳️ 四、实验验证✳️ 4.1 基于神经网络双线…
阅读更多...
Hive、Impala、Hue集成LDAP

Hive、Impala、Hue集成LDAP

1.LDAP简介 轻型目录访问协议&#xff0c;是一个开放的&#xff0c;中立的&#xff0c;工业标准的应用协议&#xff0c;通过IP协议提供访问控制和维护分布式信息的目录信息。在hadoop生态圈中&#xff0c;LDAP主要是用来做账号管理的。 2.LDAP安装配置 2.1 安装LDAP&#xf…
阅读更多...
基于PHP+MYSQL宠物领养系统的开发与设计

基于PHP+MYSQL宠物领养系统的开发与设计

市面上的宠物之家网站大多只是给爱宠人士一个交流的平台,给爱宠人士一个学习宠物习性,宠物购买的一个集合性的平台。很少有宠物领养功能,然而现在社会上有着太多的流浪宠物需要得到人们的关爱,这是很多宠物之家网站没有做到的。宠物之家网站正是顺应了当下的宠物热潮,为广大消费…
阅读更多...
LeetCode | 1851.包含每个查询的最小区间

LeetCode | 1851.包含每个查询的最小区间

LeetCode | 1851.包含每个查询的最小区间 给你一个二维整数数组 intervals &#xff0c;其中 intervals[i] [lefti, righti] 表示第 i 个区间开始于 lefti 、结束于 righti&#xff08;包含两侧取值&#xff0c;闭区间&#xff09;。区间的 长度 定义为区间中包含的整数数目&…
阅读更多...
基于java+ssm+shiro的出租房管理平台

基于java+ssm+shiro的出租房管理平台

✌博主介绍✌:一个致力于全战开发的代码热爱者 龙门客栈管理平台一、前言介绍&#xff1a;二、系统设计&#xff1a;2.1 系统整体架构&#xff1a;2.1.1 数据库表结构的介绍&#xff1a;2.1.2 系统功能设计&#xff1a;三、功能截图&#xff1a;3.1 登录注册&#xff1a;3.2 基…
阅读更多...
使用react-grid-layout和echarts-for-react实现一个支持拖拽的自定义响应式dashboard页面

使用react-grid-layout和echarts-for-react实现一个支持拖拽的自定义响应式dashboard页面

使用react-grid-layout和echarts-for-react实现一个支持拖拽的自定义响应式dashboard页面 需求概要 在前端工作中&#xff0c;我们会经常遇到自定义dashboard页这样的需求。然后我想做一个能够让用户可以在面板上自由的拖拽&#xff0c;固定&#xff08;不允许拖拽&#xff0…
阅读更多...
游戏源码编程软件，对于新手来说十分友好，纯中文的界面让所有功能都一目了然，操作相当简单

游戏源码编程软件，对于新手来说十分友好，纯中文的界面让所有功能都一目了然，操作相当简单

这是一款免费的图像化编程工具，使用者无需会任何编程语言即可通过拼接积木的形式搭建出属于自己的程序。 编程猫kitten使用教程： 1、打开软件，进入软件主界面，运行界面如下图。 2、点击文件，可选择打开、新建、打开本地作品等。 3、可在方框内输入作品名称，快速进行输入…
阅读更多...
安静！听听AI眼中岛国老师的声音~

安静！听听AI眼中岛国老师的声音~

大家好&#xff0c;我是鸟哥。一个半路出家的程序员。 最近在折腾自己的微信机器人&#xff0c;除了自动回复&#xff0c;自动拉群等常规的功能外&#xff0c;我准备给它赋予一些AI功能&#xff0c;毕竟这两年人工智能火的一塌糊涂。例如前段时间风靡朋友圈的人物头像动漫化&am…
阅读更多...
如何保存/同步多架构容器 Docker 镜像

如何保存/同步多架构容器 Docker 镜像

前言 随着容器、芯片技术的进一步发展&#xff0c;以及绿色、节能、信创等方面的要求&#xff0c;多 CPU 架构的场景越来越常见。典型的应用场景包括&#xff1a; 信创&#xff1a;x86 服务器 鲲鹏 ARM 等信创服务器&#xff1b;个人电脑&#xff1a;苹果 Mac M1 Windows 电…
阅读更多...
Triton Inference Server 环境配置

Triton Inference Server 环境配置

本人环境 Ubuntu18.04&#xff0c;3090显卡&#xff0c;显卡驱动版本510.85.02&#xff0c;cuda版本11.6&#xff0c;docker版本20.10.12(注意&#xff1a;docker一定要通过apt安装&#xff0c;用snap安装会报错) 安装步骤 1. 根据驱动版本和cuda版本下载对应版本的Triton D…
阅读更多...
java计算机毕业设计ssm驾校预约考试管理系统a3cf7（附源码、数据库）

java计算机毕业设计ssm驾校预约考试管理系统a3cf7（附源码、数据库）

java计算机毕业设计ssm驾校预约考试管理系统a3cf7&#xff08;附源码、数据库&#xff09; 项目运行 环境配置&#xff1a; Jdk1.8 Tomcat8.5 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#…
阅读更多...
第四章. Pandas进阶—日期数据处理

第四章. Pandas进阶—日期数据处理

第四章. Pandas进阶 4.7 日期数据处理 1.DataFrame的日期数据转换&#xff08;to_datetime&#xff09; 在日常工作中&#xff0c;常见的日期方式有很多种&#xff0c;例如’20221123’&#xff0c;‘2022.11.23’&#xff0c;‘2022/11/23’&#xff0c;‘23/11/2022’&#…
阅读更多...
Deepwalk详解

Deepwalk详解

算法思想 源于word2vec &#xff0c;word2vec通过语料库中的句子序列来描述词与词之间的共现关系。进而学习到词语的向量表示&#xff0c;deepwalk则使用图中的节点与节点的共像现关系来学习节点的向量表示。这种借鉴的前提是点在图中的分布和词在句子中的分布都是幂律分布。 …
阅读更多...
关于MuLoginWebGL介绍说明：

关于MuLoginWebGL介绍说明：

WebGL就是俗称的硬件显卡型号的意思&#xff0c;在MuLogin中我们提供了多个平台和品牌的显卡芯片指纹。 我们在做实验时&#xff0c;Chrome浏览器和Internet Explorer&#xff08;Edge&#xff09;测试取WebGL vendor 会有两种不同值 &#xff0c;Chrome 取为 Google Inc. Int…
阅读更多...
2023年湖北监理工程师考试科目有哪些？考试题型什么样子的？

2023年湖北监理工程师考试科目有哪些？考试题型什么样子的？

2023年湖北监理工程师考试科目有哪些&#xff1f;考试题型什么样子的&#xff1f; 一、监理工程师考试科目&#xff1a; 监理工程师考试一共考四科 1. 《建设工程监理基本理论和相关法规》(客观题) 2. 《建设工程合同管理》(客观题) 3. 《建设工程目标控制》(客观题) 4. 《…
阅读更多...
社交电商时代，切勿剑走偏锋，始终以产品为中心，模式为辅助

社交电商时代，切勿剑走偏锋，始终以产品为中心，模式为辅助

社交电商这个名词近期十分火&#xff0c;参与这个方式的人数以亿计&#xff0c;可以这样说“十亿人民九亿商&#xff0c;八亿人在做电商”。 我们感悟&#xff1a;“传统电商火热&#xff0c;社交电商更火”&#xff01;那么什么是社交电商呢&#xff1f;社交电商概念&#xff…
阅读更多...
必须了解的海外新闻稿写作要点 ️

必须了解的海外新闻稿写作要点 ️

随着经济全球化的发展&#xff0c;中国企业走向世界是必然的趋势。媒介易小编发现了全球的海外消费者一般了解一个品牌都是去搜索引擎搜索&#xff0c;所以确认海外媒体投放新闻稿是中国企业走向世界必经之路&#xff0c;是密不可分的哟。 新闻稿是公司或机构向媒体发送的手稿。…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023