Value Iteration Algorithm

其算法思想是: 在每一个状态s下，
之迭代算法流程如下：
初始化状态价值state value，即对每个状态的价值都赋一个初始值，一般是0
计算每一个状态-动作对的动作价值函数，通常通过创建一个二维表格，称为q表格
对每个状态s，最优策略 $a^*=\argmax_a q(s,a)$
策略更新： $\pi(a \mid s)=1$ if $a=a^*$
价值更新：

policy update:
$\pi_{k+1}(s)=\arg \max _{\pi} \sum_{a} \pi(a \mid s) \underbrace{\left(\sum_{r} p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_{k}\left(s^{\prime}\right)\right)}_{q_{k}(s, a)}, \quad s \in \mathcal{S}$

value update
$v_{k+1}(s)=\sum_{a} \pi_{k+1}(a \mid s) \underbrace{\left(\sum_{r} p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_{k}\left(s^{\prime}\right)\right)}_{q_{k}(s, a)}, \quad s \in \mathcal{S}$
因为这里的 $\pi_{k+1}$ 是贪婪方法，所以上式可以简化成：
$v_{k+1}(s)=\max_a q_k(a,s)$
在这里插入图片描述
步骤1：更新策略，求 $\pi_{k+1}$

一个例子

下图是一个例子，如何在一个2*2网格世界中，找到任何一个网格到蓝色方格的最短路径，即寻找最优策略pi。

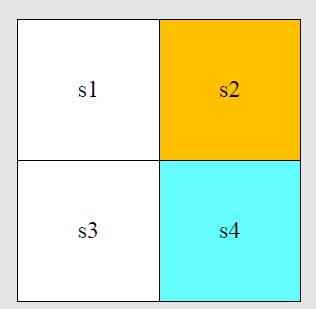
状态空间 $S=\{s_i\}_{i=1}^4$ ；
动作空间 $A=\{a_i\}_{i=1}^5$ ， $a_1$ (向上移动)， $a_2$ (向右移动)， $a_3$ (向下移动)， $a_4$ (向左移动)， $a_5$ (原地不动)；
奖励为： $r_{boundary}=r_{forbidden}=-1,r_{target}=1$ ；
折扣率 $\gamma=0.9$

手推求解

初始化所有 $v(s_i)=0,i=1,2,3,4$
初始化q表格，根据动作价值函数 $q (s, a)$ 表达式写出q表格如下：

第1轮迭代：

令 $v_0(s_1)=v_0(s_2)=v_0(s_3)=v_0(s_4)=0$ ，将 $v_0(s_i)$ 带入刚才的q表格，有：

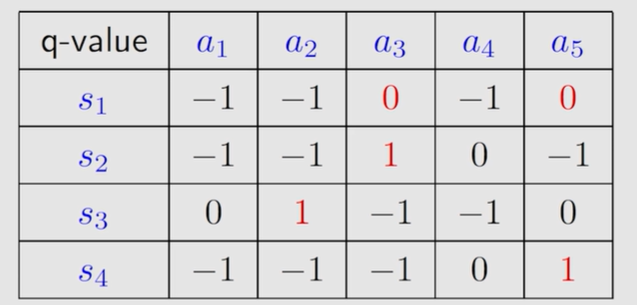
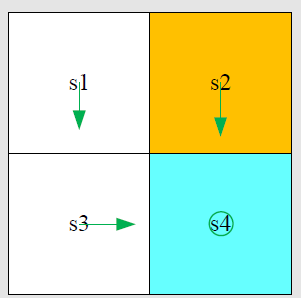
有了上方表格，可以进行Policy update，并将该策略绘制出来：
$\pi_1(a_5 \mid s_1)=1$
$\pi_1(a_3 \mid s_2)=1$
$\pi_1(a_2 \mid s_3)=1$
$\pi_1(a_5 \mid s_4)=1$

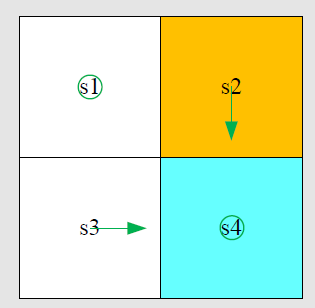
有了策略可以进行Value update：
$v_1(s_1)=0$
$v_1(s_2)=1$
$v_1(s_3)=1$
$v_1(s_4)=0$

继续迭代k=1，将 $v_1(s_i)$ 的值，带入q表格中：

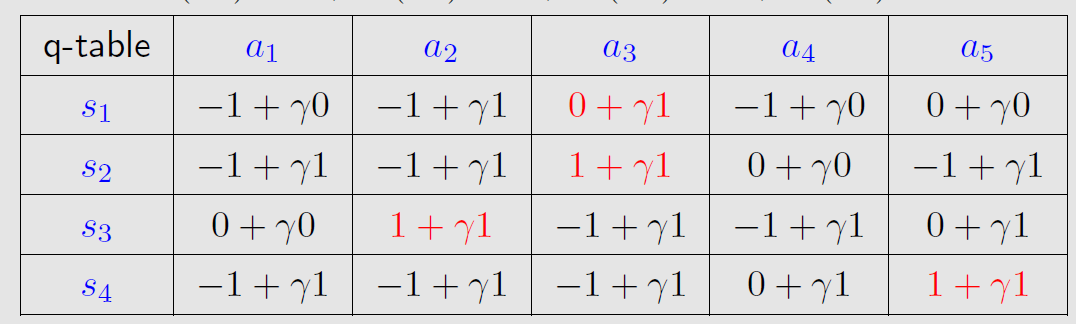
有了上方表格，可以进行Policy update，并将该策略表示出来：
$\pi_2(a_3 \mid s_1)=1$
$\pi_2(a_3 \mid s_2)=1$
$\pi_2(a_2 \mid s_3)=1$
$\pi_2(a_5 \mid s_4)=1$

有了策略可以进行Value update：
$v_2(s_1)=\gamma1=0.9$
$v_2(s_2)=1+\gamma=1.9$
$v_2(s_3)=1+\gamma=1.9$
$v_2(s_4)=1+\gamma=1.9$

此时，肉眼观察，已经得出最优策略。在编程时，则需要继续迭代k=2,3,…，直至 $||v_k-v_{k+1}||<\varepsilon,\varepsilon \to 0$

2 编程求解

定义网格世界GridWorld如下图，求解每个状态的价值函数。
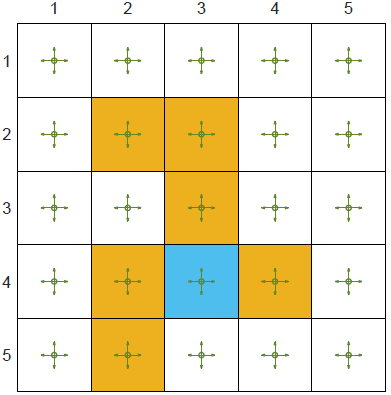
在这里插入图片描述
状态空间：

`{0: (0, 0), 1:  (0, 1), 2:  (0, 2), 3:  (0, 3), 4:  (0, 4), 
  5: (1, 0), 6:  (1, 1), 7:  (1, 2), 8:  (1, 3), 9:  (1, 4), 
 10: (2, 0), 11: (2, 1), 12: (2, 2), 13: (2, 3), 14: (2, 4), 
 15: (3, 0), 16: (3, 1), 17: (3, 2), 18: (3, 3), 19: (3, 4), 
 20: (4, 0), 21: (4, 1), 22: (4, 2), 23: (4, 3), 24: (4, 4)}`

动作空间：有5种动作，上右下左，不动

{0: '↑', 1: '→', 2: '↓', 3: '←', 4: '○'}

import numpy as np

class GridWorldEnv:

    def __init__(self, isSlippery=False):
        self.seed = np.random.seed(47)
        self.shape = (5, 5)
        self.gridWorld = np.zeros(shape=self.shape, dtype=np.int64)
        self.forbiddenGrid = [(1, 1), (1, 2), (2, 2), (3, 1), (3, 3), (4, 1)]
        self.targetGrid = (3, 2)

        self.stateSpace = self.initStateSpace()
        self.actionSpace = {0: "↑", 1: "→", 2: "↓", 3: "←", 4: "○", }

        self.action_dim = len(self.actionSpace)
        self.state_dim = np.prod(self.shape)
        self.buildGridWorld()
        self.curState = 0

        print("状态空间", self.stateSpace)
        print("动作空间", self.actionSpace)
        print("网格世界\n", self.gridWorld)

    def buildGridWorld(self):
        for x in range(5):
            for y in range(5):
                if (x, y) in self.forbiddenGrid:
                    self.gridWorld[x][y] = -1
        self.gridWorld[3][2] = 1

    def initStateSpace(self):
        stateSpace = {}
        for x in range(5):
            for y in range(5):
                stateSpace[5 * x + y] = (x, y)

        return stateSpace

    def step(self, a):
        x, y = divmod(self.curState, 5)
        oldState = 5 * x + y

        if a == 0: x -= 1  # 上
        if a == 1: y += 1  # 右
        if a == 2: x += 1  # 下
        if a == 3: y -= 1  # 左

        reward = 0
        nextState = 5 * x + y
        done = False
        # 尝试越过边界，奖励-1
        if (x < 0 or y < 0) or (x > 4 or y > 4):
            reward = -1
            nextState = oldState
            self.curState = oldState
        # 进入forbidden区域，奖励-10
        if (x, y) in self.forbiddenGrid:
            reward = -10
            done = True
        # 达到目标点，奖励1
        if (x, y) == self.targetGrid:
            reward = 1
            done = True

        return nextState, reward, done

    def reset(self, state=None):

        if state is None:
            self.curState = 0
            return 0
        else:
            self.curState = state
            return state


class ValIter:
    def __init__(self, env: GridWorldEnv):
        self.env = env
        self.policy = np.zeros(shape=self.env.state_dim, dtype=np.int64)
        self.value = np.zeros(shape=self.env.state_dim, dtype=np.float64)
        self.q_table = np.zeros(shape=(env.state_dim, env.action_dim))
        self.trace = {"pi": [self.policy], "v": [self.value], "q_table": [self.q_table]}

    def policyUpdate(self, q_table):
        for s in self.env.stateSpace:
            self.policy[s] = np.argmax(q_table[s])
        self.trace["pi"].append(self.policy)

    def valueUpdate(self, q_table):
        for s in self.env.stateSpace:
            self.value[s] = np.max(q_table[s])
        self.trace["v"].append(self.value)
        self.trace["q_table"].append(self.q_table)

    def stateValFunc(self, s):
        return self.value[s]

    def actionValFunc(self, s, a):
        self.env.reset(s)
        next_state, reward, _ = self.env.step(a)
        return reward + 0.9 * self.stateValFunc(next_state)

    def valueIteration(self):

        iter = 0
        while True:
            for s in self.env.stateSpace.keys():
                for a in self.env.actionSpace:
                    self.q_table[s][a] = self.actionValFunc(s, a)

            old_state_val = np.sum(self.value)

            self.policyUpdate(self.q_table)
            self.valueUpdate(self.q_table)

            new_state_val = np.sum(self.value)
            iter += 1

            if np.abs(new_state_val - old_state_val) < 1e-6:
                print("iter=", iter)
                break

        pi = self.trace["pi"][-1]
        v = self.trace["v"][-1]
        q_table = self.trace["q_table"][-1]
        for s in self.env.stateSpace.keys():
            a = pi[s]
            print(self.env.actionSpace[a], end="\t")
            if (s + 1) % 5 == 0:
                print()
        for s in self.env.stateSpace.keys():
            print("%.4f" % v[s], end="\t")
            if (s + 1) % 5 == 0:
                print()
        print(q_table)


if __name__ == '__main__':
    env = GridWorldEnv()
    valIter = ValIter(env)
    valIter.valueIteration()