目录
负温度系数电压
正温度系数电压
带隙基准
小结
如何产生一个不受温度变化,保持恒定的电压基准呢?
我们假设,如果将两个具有相反温度系数(TC)的量以适当的权重相加,那么结果就会成为零温度系数,即与温度变化无关。
在半导体工艺的各种不同器件参数中,双极晶体管的特性参数被证实具有最好的重复性,并且具有能提供正温度系数和负温度系数的、严格定义的量。
负温度系数电压
双极晶体管的基极-发射极电压,或者更一般地说,PN结二极管地正向电压,具有负温度系数。
公式推导太复杂,放出推导结果:
基极-发射极电压地温度系数:
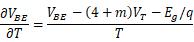
从中可以看出,温度系数与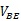 本身大小有关,与绝对温度温度T有关。当
本身大小有关,与绝对温度温度T有关。当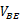 ≈750mV,T=300K时,
≈750mV,T=300K时,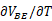 ≈ -1.5mV/K。
≈ -1.5mV/K。
正温度系数电压
如果两个双极晶体管工作在不相等的电流密度(电流密度定义为集电极电流Ic与饱和电流Is的比值)下,那么它们的基极-发射极电压的差值就与绝对温度成正比。
如下图所示:
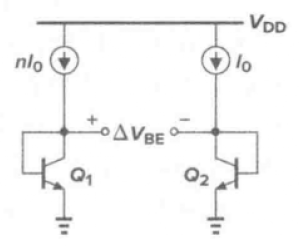
如果两个同样的晶体管(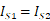 )偏置的集电极电流分别为
)偏置的集电极电流分别为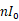 和
和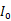 并忽略他们的基极电流,那么
并忽略他们的基极电流,那么
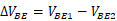
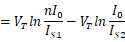
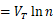
 的差值表现出的正温度系数:
的差值表现出的正温度系数:
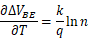
带隙基准
利用前面得到的正、负温度系数的电压,便可以设计出一个令人满意的零温度系数基准。即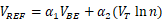 ,这里
,这里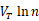 是两个工作在不同电流密度下的双极晶体管的基极-发射极电压的差值。根据负温度系数电压部分可知,在室温下,
是两个工作在不同电流密度下的双极晶体管的基极-发射极电压的差值。根据负温度系数电压部分可知,在室温下,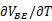 ≈-1.5mV/K;根据正温度系数电压部分算出,
≈-1.5mV/K;根据正温度系数电压部分算出,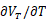 ≈+0.087mV/K,所以我们令
≈+0.087mV/K,所以我们令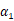 =1,选择
=1,选择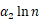 使得
使得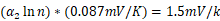 ,也就是,
,也就是,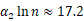 ,表明零温度系数的基准为:
,表明零温度系数的基准为:
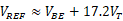
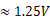
首先考虑如下图所示电路,这里假设基极电流可以忽略,晶体管Q2是由n个并联的单元晶体管组成,而Q1是一个单元晶体管。假设我们用某种方法强制VO1和VO2相等,那么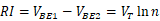 ,所以
,所以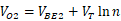 ,这就意味着:如果lnn≈17.2 ,VO2就可以作为与温度无关的基准(注:这种情况下左右两路电流是不一样的,只是保证VO1和VO2相等)。
,这就意味着:如果lnn≈17.2 ,VO2就可以作为与温度无关的基准(注:这种情况下左右两路电流是不一样的,只是保证VO1和VO2相等)。
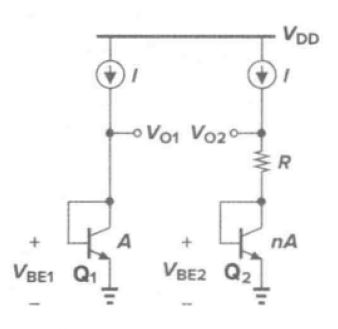
下图所示为一个可以实现上述功能的实际电路。
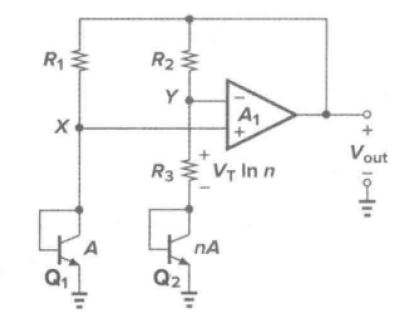
这里,放大器A1以Vx和Vy为输入,驱动R1和R2(R1=R2)的上端,使得X点和Y点稳定在近似相等的电压。基准电压可以在放大器的输出端得到而不是Y点。根据前面的分析,我们有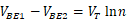 ,得到流过右边支路的电流为
,得到流过右边支路的电流为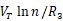 ,因此输出电压为:
,因此输出电压为:
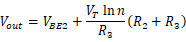
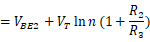
其中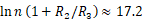 ,例如,可以选择n=31,
,例如,可以选择n=31,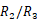 =4。
=4。
小结
根据式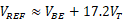 产生的电压被成为“带隙基准”,我们将输出电压写为:
产生的电压被成为“带隙基准”,我们将输出电压写为:
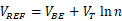
再经过各种公式代入与推导,得到:
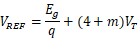
这样,额定零温度系数的电压基准就由一些基本数字给出:硅的带隙电压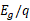 ,迁移率的温度指数m,和热电势
,迁移率的温度指数m,和热电势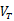 。因为当T趋近于0时,
。因为当T趋近于0时,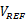 趋近于
趋近于 ,所以这里使用“带隙”这个术语。
,所以这里使用“带隙”这个术语。