说明

闵老师的文章链接：日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

day25 二叉树深度遍历的栈实现 (中序)

1.具有通用性的对象栈

package datastructure.stack;

import sun.applet.Main;

public class ObjectStack {
    /**
     * The depth.
     */
    public static final int MAX_DEPTH = 10;

    /**
     * The actual depth.
     */
    int depth;

    /**
     * The data
     */
    Object[] data;

    /**
     * Construct an empty sequential list.
     */
    public ObjectStack() {
        depth = 0;
        data = new Object[MAX_DEPTH];
    }

    /**
     * Overrides the method claimed in Object, the superclass of any class.
     * @return
     */
    public String toString() {
        String resultString = "";
        for (int i = 0; i < depth; i++) {
            resultString += data[i];
        }

        return resultString;
    }

    /**
     * Push an element.
     * @param paraObject  The given object.
     * @return Success or not.
     */
    public boolean push(Object paraObject){
        if (depth == MAX_DEPTH) {
            System.out.println("Stack full.");
            return false;
        }

        data[depth] = paraObject;
        depth++;

        return true;
    }

    /**
     * Pop an element.
     * @return The object at the top of the stack.
     */
    public Object pop() {
        if (depth == 0) {
            System.out.println("Nothing to pop.");
            return '\0';
        }

        Object resultObject = data[depth - 1];
        depth--;

        return resultObject;
    }

    /**
     * Is the stack empty?
     * @return True if empty.
     */
    public boolean isEmpty() {
        if (depth == 0) {
            return true;
        }

        return false;
    }

    public static void main(String args[]) {
        ObjectStack tempStack = new ObjectStack();

        for (char ch = 'a'; ch < 'm'; ch++) {
            tempStack.push(new Character(ch));
            System.out.println("The current stack is: " + tempStack);
        }

        char tempChar;
        for (int i = 0; i < 12; i++) {
            tempChar = ((Character)tempStack.pop()).charValue();
            System.out.println("Poped: " + tempChar);
            System.out.println("The current stack is: " + tempStack);
        }
    }

}

2.栈实现中序遍历

2.1 思路

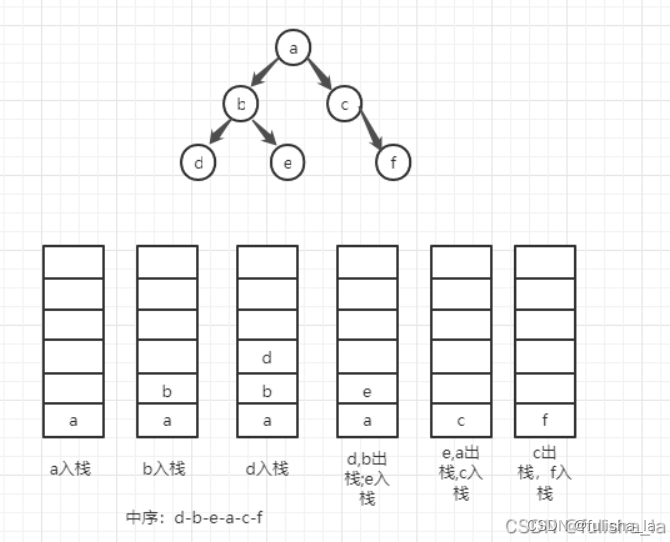
结合下图，先考虑假设一颗最简单的二叉树，一个根结点a和左右两个子结点b,c，利用栈，a，b入栈，将b出栈，判断b是否有右孩子，无则继续出栈a,再判断a是否有右孩子，有c,则将c入栈，再判断c是否有左孩子若无，再出栈,再判断c是否有右孩子，无，则顺序是b-a-c

在这里插入图片描述
由最简单的二叉树到一般二叉树，我们知道中序遍历顺序是左-根-右，结合栈，先将左子树的左节点入栈（左子树不为空），当最左节点入栈后就开始出栈，每出一个节点就要判断是否有右子树，若有则需要入栈（这又像一颗子树，又要重复和原来一样的操作，入最左结点再出栈判断出栈结点是否有右子树），操作和那最大那一棵树的操作一样。（看着图理解就一目了然了）
在这里插入图片描述

2.2 代码


    /**
     * In-order visit with stack.
     */
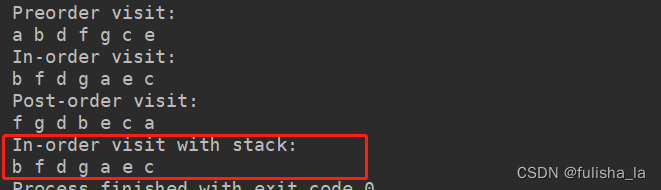
    public void inOrderVisitWithStack(){
        ObjectStack tempStack = new ObjectStack();
        BinaryCharTree tempNode = this;
        while (!tempStack.isEmpty() || tempNode != null){
            if (tempNode != null){
                tempStack.push(tempNode);
                tempNode = tempNode.leftChild;
            } else {
                tempNode = (BinaryCharTree)tempStack.pop();
                System.out.print("" + tempNode.value + " ");
                tempNode = tempNode.rightChild;
            }
        }
    }

在这里插入图片描述

day26 二叉树深度遍历的栈实现 (前序和后序)

1.前序遍历

前序遍历顺序是根-左-右，而在入栈时入栈顺序和中序是一样的，而要输出中序顺序，则需要修改一下，在push之前先输出

    /**
     * Pre-order visit with stack.
     */
    public void preOrderVisitWithStack() {
        ObjectStack tempStack = new ObjectStack();
        BinaryCharTree tempNode = this;
        while (!tempStack.isEmpty() || tempNode != null) {
            if (tempNode != null) {
                System.out.print("" + tempNode.value + " ");
                tempStack.push(tempNode);
                tempNode = tempNode.leftChild;
            } else {
                tempNode = (BinaryCharTree) tempStack.pop();
                tempNode = tempNode.rightChild;
            }
        }
    }

2.后序遍历

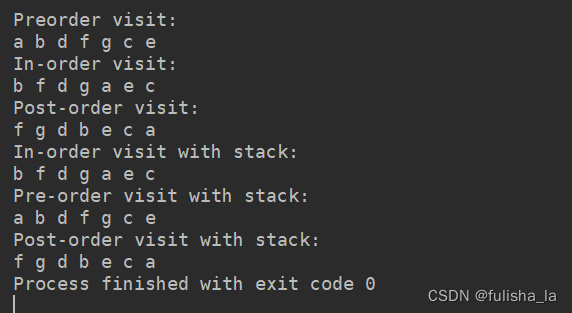
结合文章中后序遍历的两种思想，第一种是直接写，第二种是逆向思维，等价替换问题（这个思维很好，学习到了。），由前序遍历：根-左-右，交换左右子树为根-右-左，最后再将其逆序变为左-右-根。借助两个栈，一个栈和前序中序的存节点出入栈一样，这样保证入栈顺序，另一个栈是将原本需要输入的数据存入栈中（输入顺序为根-右-左），在所有节点遍历完，再将这个存出栈顺序数据的栈打印输出就是以左-右-根输出（将栈先进后出用到极致）

    /**
     * Pre-order visit with stack.
     */
    public void preOrderVisitWithStack() {
        ObjectStack tempStack = new ObjectStack();
        BinaryCharTree tempNode = this;
        while (!tempStack.isEmpty() || tempNode != null) {
            if (tempNode != null) {
                System.out.print("" + tempNode.value + " ");
                tempStack.push(tempNode);
                tempNode = tempNode.leftChild;
            } else {
                tempNode = (BinaryCharTree) tempStack.pop();
                tempNode = tempNode.rightChild;
            }
        }
    }

    /**
     * Post-order visit with stack.
     */
    public void postOrderVisitWithStack() {
        ObjectStack tempStack = new ObjectStack();
        BinaryCharTree tempNode = this;
        ObjectStack tempOutputStack = new ObjectStack();

        while (!tempStack.isEmpty() || tempNode != null) {
            if (tempNode != null) {
                //Store for output.
                tempOutputStack.push(new Character(tempNode.value));
                tempStack.push(tempNode);
                tempNode = tempNode.rightChild;
            } else {
                tempNode = (BinaryCharTree) tempStack.pop();
                tempNode = tempNode.leftChild;
            }
        }

        //Now reverse output.
        while (!tempOutputStack.isEmpty()) {
            System.out.print("" + tempOutputStack.pop() + " ");
        }
    }

在这里插入图片描述