Cheaptrick，a spectral envelope estimator for high-qualityspeech synthesis

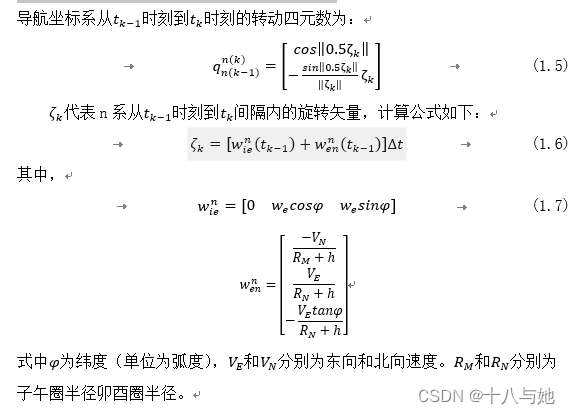
转载请注明出处！

2015年Morise发表在SPEECH COMMUNICATION期刊上的一篇文章。

该算法目的是获得一个准确的、时间稳定的谱包络，采用基频(F0)，由F0自适应加窗、功率谱平滑和频率域频谱恢复三部分组成。

引言

一些估计算法，如倒谱(Noll, 1964;Oppenheim, 1969)和线性预测编码(LPC) (Atal和Hanauer, 1969)及许多改进的算法，如离散全极建模(El-Jaroudi和Makhoul,1991)，加权最大似然自回归和移动平均建模(Badeau和David, 2009)，以及惩罚似然方法(Campedel-Oudot等人，2001)。但是这些算法合成的语音音质比使用PSOLA等基于波形的合成方法要差，很难实现高质量的语音转换。
STRAIGHT (Kawahara et al.1999)被认为是一种有效的高质量语音合成框架。为了在保持音质的同时减少计算成本，提出了TANDEM_STRAIGHT，在庞大的数据库可实现实时应用(Morise et al.， 2009)和统计分析。

待解决问题

根据STRAIGHT的思想，浊音包含F0、谱包络和非周期性信息。为了简化讨论，我们只处理固定的F0和谱包络，而忽略非周期性。要求从语音波形中获得精确的频谱包络，而不考虑加窗的时间位置。
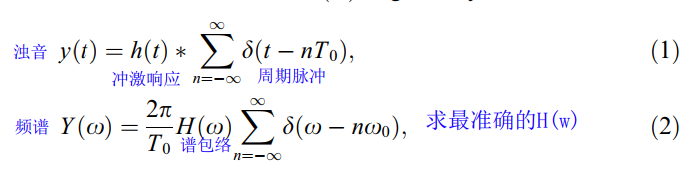
在这里插入图片描述
*表示卷积，T0是基音周期，w0是基本角频率（=2Π/T0）。
谱恢复还需要补偿离散化的影响。由于加窗波形的功率谱依赖于窗函数的时间位置，因此也需要去除这种影响(本文中的时变分量)。
传统算法除了STRAIGHT算法和TANDEM-STRAIGHT，在估计性能上不能满足这两个要求，并且不能去除时变分量。本文介绍了一种算法
它在客观上和主观上都优于传统算法。CheapTrick的名字来源于它基于f0自适应窗口和倒谱方法等传统算法的cheap和trick的设计。

Cheaptrick算法

CheapTrick由三个步骤组成:f0自适应窗口，平滑功率谱，以及平滑和频谱恢复的提升处理。

第一步：计算F0自适应功率谱

第一步是在基音同步分析的理想基础上设计窗口函数(Mathews et al.， 1961)。

（1）加窗
该算法采用长度为3T0的汉宁窗。

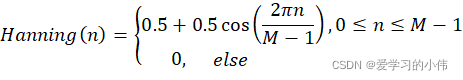
在这里插入图片描述
窗口在ω0 Hz处的功率比主瓣的功率(0 Hz)低30 dB，这表明在30 dB以下谐波结构对邻近结构有影响。由于实际语音包含时间波动、非周期性和噪声，我们假设30 dB足够小。

waveform = GetWindowedWaveform(x, fs, current_f0, current_position);

function waveform = GetWindowedWaveform(x, fs, current_f0, current_position)
%  prepare internal variables
half_window_length = round(1.5 * fs / current_f0);%1169=round(1.5 * 88200 / 113.21)
base_index = (-half_window_length : half_window_length)';%2339*1 = (-1169 : 1169)'
index = round(current_position * fs + 0.001) + 1 + base_index;%2339*1 = round(0*88200+0.001)+1+2339*1(所有值全加1)
safe_index = min(length(x), max(1, round(index)));% 只取2339*1？ 

%  wave segments and set of windows preparation
segment = x(safe_index);
time_axis = base_index / fs / 1.5;
window = 0.5 * cos(pi * time_axis * current_f0) + 0.5;
window = window / sqrt(sum(window .^ 2));
waveform = segment .* window - window * mean(segment .* window) / mean(window);

周期信号y(t)经过加窗w(t)，计算功率谱：

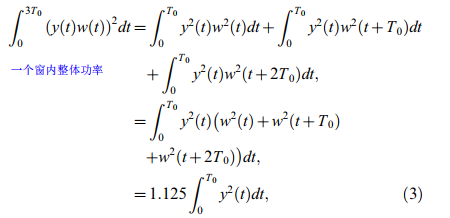
在这里插入图片描述
T0是基音周期。该方程表明，一个窗内的周期信号的总功率是时间稳定的。

power_spectrum = GetPowerSpectrum(waveform, fs, fft_size, current_f0);

function power_spectrum = GetPowerSpectrum(waveform, fs, fft_size, f0)
power_spectrum = abs(fft(waveform(:), fft_size)) .^ 2;
% DC correction
frequency_axis = (0 : fft_size - 1)' / fft_size * fs;
low_frequency_axis = frequency_axis(frequency_axis <  f0 + fs / fft_size);
low_frequency_replica = interp1(f0 - low_frequency_axis,...
  power_spectrum(frequency_axis < f0 + fs / fft_size),...
  low_frequency_axis(:), 'linear', 'extrap');
power_spectrum(frequency_axis < f0) =...
  low_frequency_replica(frequency_axis < f0) +...
  power_spectrum(frequency_axis < f0);
power_spectrum(end : -1 : fft_size / 2 + 2) = power_spectrum(2 : fft_size / 2);

第二步：功率谱平滑

log0的值是负无穷，所以需保证log域的功率不能为0。
通过一个矩形窗进行简单滤波来实现平滑：
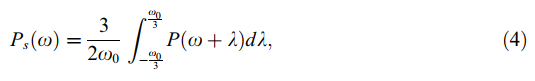
在这里插入图片描述
P(ω)是加汉宁窗的功率谱。由于矩形窗宽为2ω0/3，这一步确保了与第一步一样相邻结构之间的影响小于30db。

smoothed_spectrum = LinearSmoothing(power_spectrum, current_f0, fs, fft_size);

function smoothed_spectrum = LinearSmoothing(power_spectrum, f0, fs, fft_size)
double_frequency_axis = (0 : 2 * fft_size - 1)' / fft_size * fs - fs;
double_spectrum = [power_spectrum; power_spectrum];

double_segment = cumsum(double_spectrum * (fs / fft_size));
center_frequency = (0 : fft_size / 2)' / fft_size * fs;
low_levels = interp1H(double_frequency_axis + fs / fft_size / 2,...
  double_segment, center_frequency - f0 / 3);
high_levels = interp1H(double_frequency_axis + fs / fft_size / 2,...
  double_segment, center_frequency + f0 / 3);

smoothed_spectrum = (high_levels - low_levels) * 1.5 / f0;
smoothed_spectrum =...
  smoothed_spectrum + abs(randn(length(smoothed_spectrum), 1)) * eps;

第三步：倒频域提升

目的：去除离散化引起的频率波动。同时进行了光谱恢复。
时变分量是由周期脉冲卷积和加窗引起的。

时域：周期为T0的周期脉冲
频域：谱是周期为ω0的周期脉冲
倒谱：也是倒频率域内周期为T0的周期脉冲，如下图
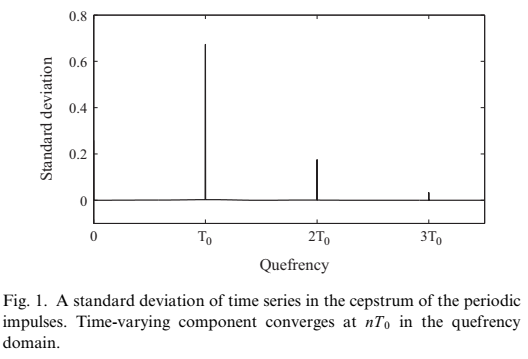
在这里插入图片描述
为了明确计算nT0处的时变分量，信号的采样频率为65536 Hz, F0为128 Hz, FFT长度为65,536，信号长度为1 s，帧移长度为一个样本。
为了去除时变分量和提取低定量分量，采用sinc函数作为提升函数。
谱恢复基于一致采样理论(Unser, 2000)。一致采样理论是采样理论的扩展，要求AD转换后的数字信号必须等于AD/DA/AD转换后的数字信号。这种采样使线性滤波器的设计能够满足这一要求。
在一致性采样的基础上，设计了提升功能作为补偿滤波器。该函数可以补偿nω0 Hz处的误差，这些误差是由第二步和第三步平滑引起的。

TANDEM-STRAIGHT的频域上进行了基于一致采样的谱恢复(Kawahara et al.， 2008)：
在这里插入图片描述
本文的提升恢复谱计算方法如下：

频域矩形窗，该窗在图2所示的quefency域的nT0处为零。
试错实验，得到q0=1.18, q1=-0.09。

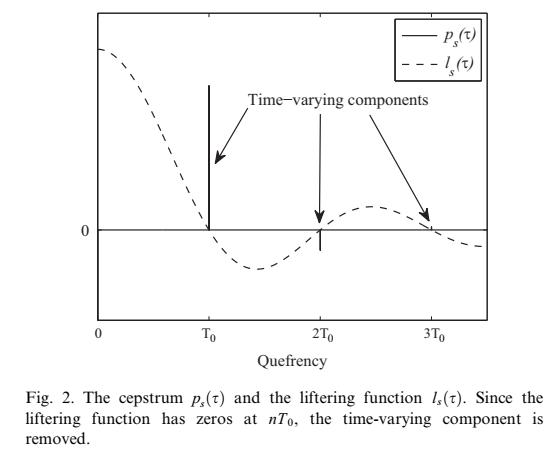
在这里插入图片描述
每个处理都是在离散时频表示上进行的。Pl(k,n)，其中k表示离散频率索引，n表示帧数。

spectral_envelope = SmoothingWithRecovery(...
  [smoothed_spectrum; smoothed_spectrum(end - 1 : -1 : 2)], current_f0, fs,...
  fft_size, q1);


function spectral_envelope =...
  SmoothingWithRecovery(smoothed_spectrum, f0, fs, fft_size, q1)
quefrency_axis = (0 : fft_size - 1)' / fs;
smoothing_lifter = sin(pi * f0 * quefrency_axis) ./ (pi * f0 * quefrency_axis);
smoothing_lifter(fft_size / 2 + 2 : end) =...
  smoothing_lifter(fft_size / 2 : -1 : 2);
smoothing_lifter(1) = 1;

compensation_lifter =...
  (1 - 2 * q1) + 2 * q1 * cos(2 * pi * quefrency_axis * f0);
compensation_lifter(fft_size / 2 + 2 : end) =...
  compensation_lifter(fft_size / 2 : -1 : 2);
tandem_cepstrum = fft(log(smoothed_spectrum));
tmp_spectral_envelope =...
  exp(real(ifft(tandem_cepstrum .* smoothing_lifter .* compensation_lifter)));
spectral_envelope = tmp_spectral_envelope(1 : fft_size / 2 + 1);