来源:力扣(LeetCode)
描述:
给定二叉树的根节点 root,找出存在于 不同 节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
示例 1:
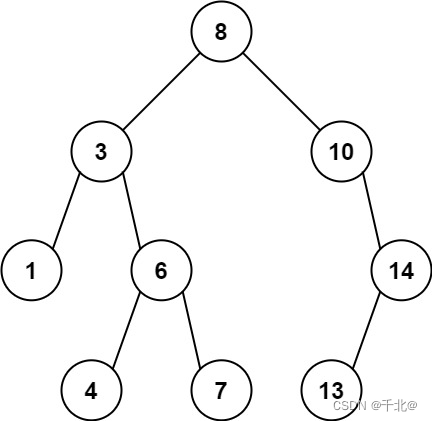
输入:root = [8,3,10,1,6,null,14,null,null,4,7,13]
输出:7
解释:
我们有大量的节点与其祖先的差值,其中一些如下:
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
在所有可能的差值中,最大值 7 由 |8 - 1| = 7 得出。
示例 2:
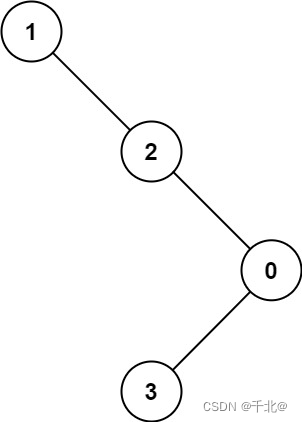
输入:root = [1,null,2,null,0,3]
输出:3
提示:
- 树中的节点数在 2 到 5000 之间。
- 0 <= Node.val <= 105
方法:深度优先搜索
题目要求找出所有祖先节点与它的子孙节点的绝对差值的最大值。按照枚举的思路,我们可以枚举子孙节点,然后找出它的所有祖先节点,计算绝对差值。同样地,我们也可以枚举祖先节点,然后找出它的所有子孙节点,计算绝对差值。
以第一种思路为例,并非所有祖先节点都需要被考虑到,我们只需要获取最小的祖先节点以及最大的祖先节点。我们对二叉树执行深度优先搜索,并且记录搜索路径上的节点的最小值 mi 与最大值 ma。假设当前搜索的节点值为 val,那么与该子孙节点与它的所有祖先节点的绝对差值最大值为 max(∣val − mi∣, ∣val − ma∣),搜索该节点的左子树与右子树时,对应的 mi = min(mi, val),ma = max(ma, val)。
- 为什么只需要获取最小的祖先节点以及最大的祖先节点?
假设某一子孙节点为 x,对应的最小的祖先节点为 mi,最大的祖先节点为 ma。有任一祖先节点为 y,显然 mi ≤ y ≤ ma。如果 x ≤ y,那么 ∣x − y∣ = y − x ≤ ma − x = ∣x − ma∣,如果 x > y,那么 ∣x − y∣= x − y ≤ x − mi =∣x − mi∣,因此最大的绝对差值与祖先节点 y 无关。
第二种思路是否可行?
可行,需要返回当前子树的最小值和最大值,方法类似。
代码:
class Solution {
public:
int dfs(TreeNode *root, int mi, int ma) {
if (root == nullptr) {
return 0;
}
int diff = max(abs(root->val - mi), abs(root->val - ma));
mi = min(mi, root->val);
ma = max(ma, root->val);
diff = max(diff, dfs(root->left, mi, ma));
diff = max(diff, dfs(root->right, mi, ma));
return diff;
}
int maxAncestorDiff(TreeNode* root) {
return dfs(root, root->val, root->val);
}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:10.4 MB, 在所有 C++ 提交中击败了34.05%的用户
复杂度分析
时间复杂度:O(n),其中 n 是二叉树的节点数目。遍历二叉树的所有节点需要 O(n)。
空间复杂度:O(n)。最坏情况下,二叉树退化为链表,递归栈的空间为 O(n)。
author:LeetCode-Solution