一、InnoDB 中的索引方案

1. 聚簇索引

聚簇索引 有两个特点：

1. 使用记录主键值的大小进行记录和页的排序，这包括3方面的含义.

   （1）页〈包括叶子节点和内节点〉内的记录按照主键的大小顺序排成一个单向链表，页内的记录被划分成若干个组，每个组中主键值最大的记录在页内的偏移量会被当作槽依次存放在页目录中(当然 Supremum 录比任何用户记录都大) ，我们可以在页目录中通过二分法快速定位到主键列等于某个值的记录。
   （2）各个存放用户记录的页也是根据页中用户记录的主键大小顺序排成一个双向链表。
   （3）存放目录项记录页分为不同的层级， 在同一层级中的页也是根据页中目录项记录的主键大小顺序排成一个双向链表。

2. B+ 树的叶子节点存储的是完整的用户记录。
   所谓完整的用户记录，就是指这个记录中存储了所有列的值(包括隐藏列)。

我们把具有这两个特点的 B+ 树称为聚簇索引，所有完整的用户记录都存放在这个聚簇索引的叶子节点处。这种聚簇索引并不需要我们在 SQL 语句中显式地使用 INDEX 语句去创建(后边会介绍索引相关的语句)，InnoDB 存储引擎会自动为我们创建聚簇索引。另外有趣的一点是，在 InnoDB 存储引擎中，聚簇索引就是数据的存储方式(所有的用户记录都存储在了叶子节点) ，也就是所谓的"索引即数据，数据即索引"。

2. 二级索引

1） 二级索引（或，辅助索引）

以非主键列的大小为排序规则而建立的B+树需要执行回表操作才可以定位到完整的用户记录，这种 B+ 树也称为二级索引 (Secondary Index) 或辅助索引。

2）索引列

由于我们是c2 列的大小作为 B+ 树的排序规则，所以我们也称这棵 B+ 树为 c2 列建立的索引，把 c2列称为索引列。

3）回表

1. 回表：通过携带主键信息 到 聚簇索引中 重新定位完整的用户记录的过程。

2. 为什么还需要一次回表操作呢?直接把完整的用户记录放到叶子节点不就好了么?你说得对，如果把完整的用户记录放到叶子节点是可以不用回表，但是太占地方了 一相当于每建立一棵B+树都需要把所有的用户记录复制一遍，这就太浪费存储空间了。

3. 应用： 以非主键列的大小为排序规则而建立的 B+ 树需要执行回表操作才可以定位到完整的用户记录。

4）二级索引、聚簇索引 异同

二级索引记录和聚簇索引记录使用的是一样的记录行格式，只不过二级索引记录存储的列不像聚簇索引记录那么完整。
聚簇索引或者二级索引的叶子节点中的记为用户记录。为了区分，

• 聚簇索引叶子节点中的记录称为完整的用户记录。

  •  完整的用户记录：指这个记录中存储了所有列的值(包括隐藏列)。
    

• 二级索引叶子节点中的记录称为不完整的用户记录。

3. 联合索引

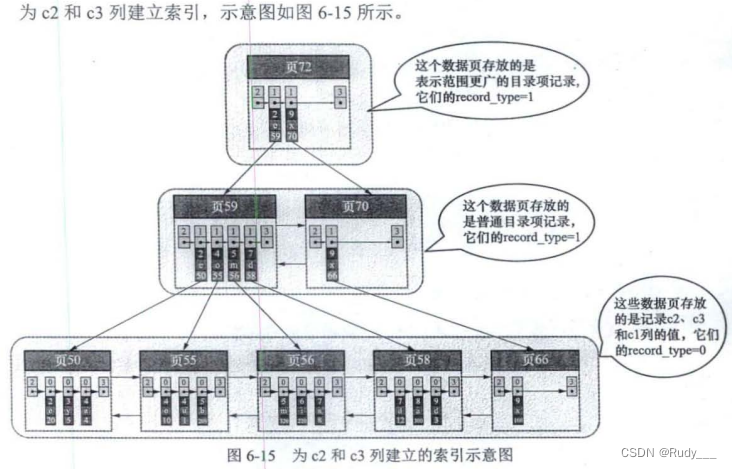
以c2列和c3列的大小为排序规则建立的 B+ 树称为联合索引，也称为复合索引或多列索引。它本质上也是一个二级索引，它的索引列包括 c2、c3。

注意：“以c2和c3列的大小为排序规则建立联合索引” 和 "分别为c2和c3列建立索引” 的表述是不同的，不同点如下.

• 建立联合索引只会建立如图 6-15 所示的一棵 B+ 树.
• 为c2和c3列分别建立索引时，则会分别以 c2 和 c3 列的大小为排序规则建立两棵 B+ 树.
  

4. InnoDB 中 B+ 树索引的注意事项

1） 根页面万年不动窝

一个 B+ 树索引的根节点自创建之日起便不会再移动(也就是页号不再改变)。

2） 内节点中目录项记录的唯一性

二级索引的内节点的目录项记录的内容实际上是由三部分构成的:

 - 索引列的值 
 - 主键值
 - 页号。

	对于二级索引记录来说，是先按照二级索引列的值进行排序，
	在二级索引列值相同的情况下，再按照主键值进行排序。

3）一个页面至少容纳2条记录

为了避免 B+ 树的层级增长得过高。

二、MylSAM 中的索引方案 和 InnoDB 中的索引方案 对比

1） 结构

• lnnoDB 中索引即数据，也就是聚簇索引的那棵 B+ 树的叶子节点中已经包含了
  所有完整的用户记录。
• MyISAM 中"索引是索引，数据是数据”。 MyISAM 索引方案虽然也使用树形结构，但是却将索引和数据分开存储。
  • 将表中的记录按照记录的插入顺序单独存储在一个文件中(称之为数据文件)。这个文件并不划分为若干个数据页 ，有多少记录就往这个文件中塞多少记录。这样一来，我们可以通过行号快速访问到一条记录。
  • 使用 MyISAM 存储引擎的表会把索引信息单独存储到另外一个文件（称为索引文件)。 MyISAM 会为表的主键单独创建一个索引，只不过在索引的叶子节点中存储的不是完整的用户记录，而是主键值与行号的组合。也就是先通过索引找到对应的行号再通过行号去找对应的记录。

2） 查询方式

• 在 InnoDB 存储引擎中，我们只需要根据主键值对聚簇索引进行一次查找就能找到对应的记录。
• 而在 MyISAM 中却需要进行一次回表操作，这也意味着 MyISAM 中建立的索引相当于全部都是二级索引。
  • 如果有必要，我们也可以为其他列分别建立索引或者建立联合索引，其原理与lnnoDB中的索引差不多，只不过在叶子节点处存储的是相应的列+行号。这些索引也全部都是二级索引。
  • MyISAM 的行格式有定长记录格式 （Static）、变长记录格式 （Dynamic） 压缩记录格式( Compressed )等。
    • 定长记录格式，指记录占用的存储空间是固定的。这样就可以使用行号轻松算出某条记录在数据文件中的地址偏移量了。
    • 变长记录格式， MyISAM 直接在索引叶子节点处存储该条记录在数据文件中的地址偏移量。此可以看出， MyISAM 的回表操作是十分快速的，因为它是拿着地址偏移量直接到文件中取数据，而InnoDB 是通过获取主键之后再去聚簇索引中找记录，虽然说也不慢，但还是比不上直接用地址去访问。

——仅做笔记，总结摘抄自《MySQL是怎样运行的》