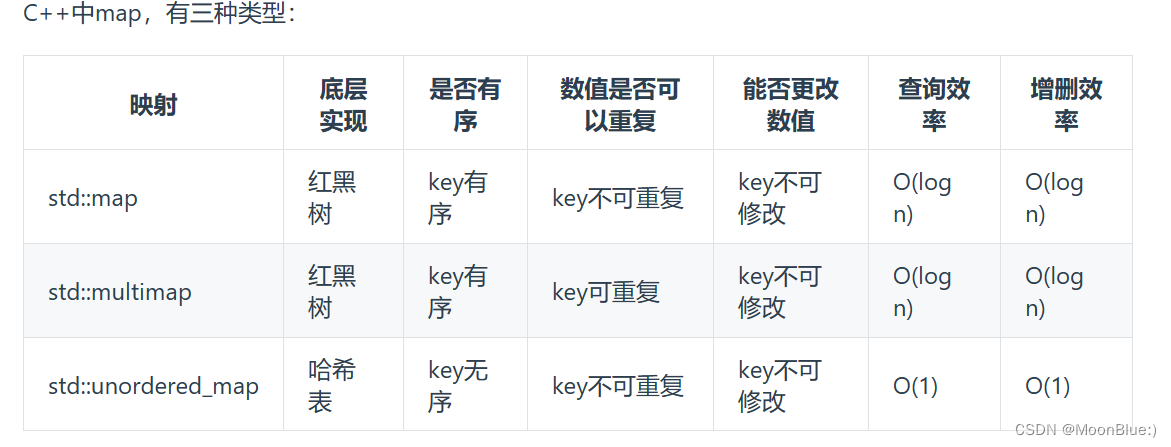
哈希表

哈希碰撞：拉链法（链表）线性探测法（顺序向后）
std::unordered_map, std::unordered_set：增删效率和查询效率都是O(1)
判断一个元素是否出现过 -> 哈希法
牺牲空间换时间，使用额外的数组，set或map存放数据

242 有效的字母异位词

思路

若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。
考虑用map结构，key为字母，value是出现次数
map中字母不能重复

代码

class Solution {
public:
    bool isAnagram(string s, string t) {
        int record[26] = {0};
        for (char c : s) {
            int num = c - 'a';
            record[num] ++;
        } 
        for (char c: t) {
            int num = c - 'a';
            record[num] --;
        }
        for (int i = 0; i < 26; i++) {
            if(record[i] != 0) {
                return false;
            }
        }
        return true;
    }
};

总结

1. 一开始我下意识用的是map，但是看了书发现是用数组，因为数组占用空间小，速度也比较快

349 两个数组的交集

思路

使用set
本题后面 力扣改了 题目描述 和 后台测试数据，增添了 数值范围：
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 1000
所以就可以 使用数组来做哈希表了， 因为数组都是 1000以内的。
直接使用set 不仅占用空间比数组大，而且速度要比数组慢，set把数值映射到key上都要做hash计算的。

代码

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result;
        unordered_set<int> s;
        for (auto num : nums1) {
            s.insert(num);
        }
        for (auto num : nums2) {
            if (s.find(num) != s.end()) {
                // 找到交集
                result.insert(num);
            }
        }
        return vector<int>(result.begin(),result.end());
    }
};

总结

1. 主要是最终结果也需要用hashset，防止结果中有重复的
2. vector<int>(s.begin(), s.end())这种写法以前没写过，记忆

202 快乐数

思路

这题自已先写的时候没思路
题目中说了会 无限循环，那么也就是说求和的过程中，sum会重复出现，这对解题很重要！当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法了。

代码

class Solution {
public:
    int getSum(int n) {
        int sum = 0;
        while (n) {
            int i = n%10;
            sum += (i*i);
            n /= 10;
        }
        return sum;
    }
    bool isHappy(int n) {
        unordered_set<int> s;
        while (n) {
            n = getSum(n);
            if (n == 1) {
                return true;
            }
            if (s.find(n) != s.end()) {
                return false;
            }
            else {
                s.insert(n);
            }
        }
        return false;
    }
};

总结

1. 对于set的使用不熟练（总是忘记要声明元素类型）

1 两数之和

思路

再来看一下使用数组和set来做哈希法的局限。

1. 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
2. set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。

代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> result(2);
        unordered_map<int,int> m;
        for (int i = 0; i < nums.size(); i++) {
            int num = nums[i];
            int tmp = target - num;
            if (m.find(tmp) != m.end()) {
                int key = m[tmp];
                result[0] = i;
                result[1] = key;
            }
            else {
                m.insert({num,i});
            }
        }
        return result;
    }
};

总结

1. unordered_map中查找value：int value = map[key];