数据结构_第十三关（2）：快速排序

news2024/11/26 10:47:06

目录

1.快速排序

原理：

 代码如下（递归实现）：

性能比较

快速排序的特性总结

2.快速排序的优化

1）三数取中优化：

2）小区间优化：

3. 挖坑法（快排的另一种思路）：

4. 快慢指针法（快排的第三种思路）：

5.快速排序（非递归版代码）

6.源代码（VS2022下编写）

1.快速排序

基本思想：

任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止

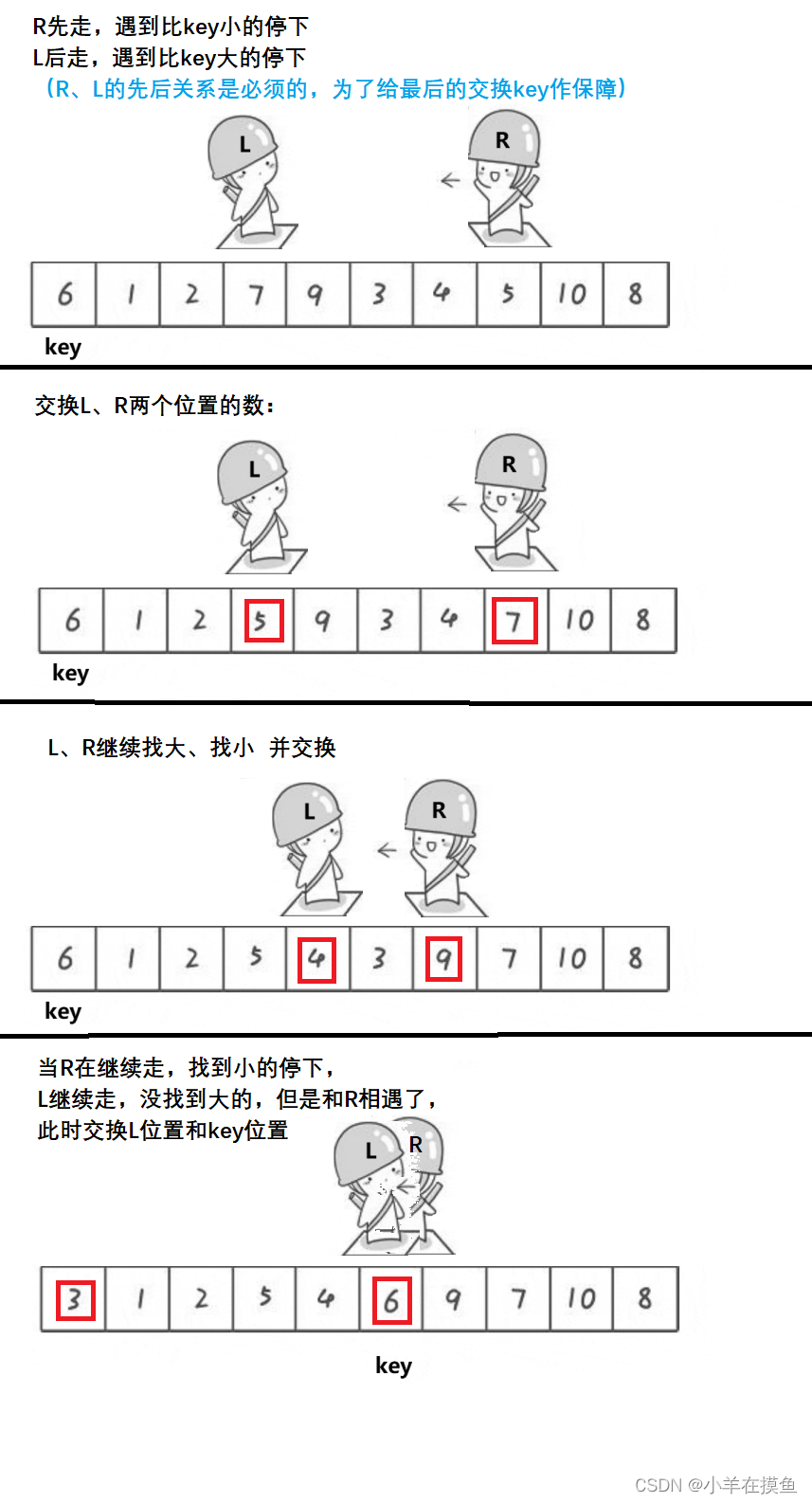
原理：

如上述图所示，此时就完成了一次单趟排序

单趟排序的作用：

  1. 使得key到了准确的位置
  2. 使得key左边的数都小于key，key右边的数都大于key

剩下的问题：让左区间有序、有区间有序，整体就ok了

然后再对其递归排序数组key的左边和右边，最终就可排好序

注意的点：

  • 左边和右边都可以做key，但是
  • 左边做key，右边要先走
  • 右边做key，左边要先走
  • 这是为了保证相遇的位置，一定比key要小（左边做key的情况下）

 代码如下（递归实现）：

这个代码写起来会有很多坑，如下，单趟排序：

正确代码： 

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	int left = begin, right = end;
	int keyi = left;
	while (left < right)
	{
		// 右边先走，找小
		while (left < right && a[right] >= a[keyi])
		{
			--right;
		}

		// 左边再走，找大
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}

	Swap(&a[left], &a[keyi]);
	keyi = left;

	// [begin, keyi-1]  keyi [keyi+1, end]
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi+1, end);
}

性能比较

和上之前的简单排序算法的效率比较如下：

 1万随机数据量下测得

  10万随机数据量下测得

 

去掉选择排序和冒泡排序， 100万随机数据量下测得

去掉直接插入排序 ， 1000万随机数据量下测得

可以看出在数据量达到1000万级别时，快速排序似乎不占优势

因为key的取值，我们可以给快排进行优化，如第二部分。

快速排序的特性总结

  1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
  2. 时间复杂度：O(N*logN)
  3. 空间复杂度：O(logN)
  4. 稳定性：不稳定

在快速排序的时间复杂度计算中，最坏情况为：

没次key都是最大或者最小的，

实际情况：有序

此时，时间复杂度为O（N^2）

快排的中心思想就是：

  • 不管你怎么选key，在第一趟排序之后，key的位置是正确的，
  • 并且，key左边的数小于key，key右边的数大于key

因为key的选择可以不同，所以快排就有了一下的改进：

2.快速排序的优化

1）三数取中优化：

 （主要对时间进行优化）

原理：

选择最左边，最中间，最右边的三个数作比较，选出最小的数作为key

代码如下：

//快排改进：key选值的三数取中
int GetMidIndex(int* a, int begin, int end)
{
	int mid = (begin + end) / 2;
	if (a[begin] < a[mid])
	{
		if (a[mid] < a[end])
		{
			return mid;
		}
		else if (a[begin] > a[end])
		{
			return begin;
		}
		else
		{
			return end;
		}
	}
	else // a[begin] > a[mid]
	{
		if (a[mid] > a[end])
		{
			return mid;
		}
		else if (a[begin] < a[end])
		{
			return begin;
		}
		else
		{
			return end;
		}
	}
}
void MidQuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	int mid = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[mid]);

	int left = begin, right = end;
	int key = left;
	while (left < right)
	{
		// 右边先走，找小
		while (left < right && a[right] >= a[key])
		{
			--right;
		}

		// 左边再走，找大
		while (left < right && a[left] <= a[key])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}

	Swap(&a[left], &a[key]);
	key = left;

	// [begin, keyi-1]  key [keyi+1, end]
	QuickSort(a, begin, key - 1);
	QuickSort(a, key + 1, end);
}

加入三数取中之后，快排的时间复杂度就可以认为是：O（N*logN）；

性能比较：

之前1000万随机数据量下测得的数据：

加入三数取中后，1000万随机数据量下测得的数据：

 可以看到，此时快排的效率有了明显的提高

2）小区间优化：

（主要对空间进行优化）

c++官方库，QST库都的快排都在用小区间优化

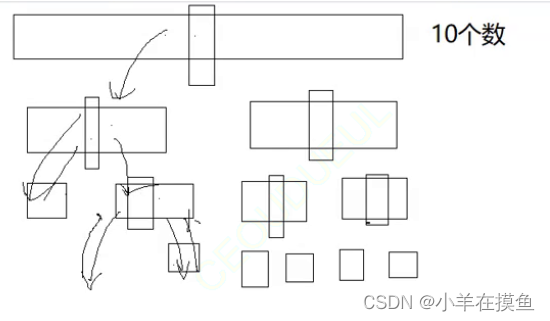
原理：

到最后10个数的时候，用递归的话，可以看到还需要4层深度的递归

 

对最后一小段区域的排序，我们用直接插入排序就行

 代码如下：

//小区间优化（优化空间）
void SpaceQuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	if ((end - begin + 1) < 10)
	{
		// 小区间用直接插入替代，减少递归调用次数
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
		int mid = GetMidIndex(a, begin, end);
		Swap(&a[begin], &a[mid]);

		int left = begin, right = end;
		int keyi = left;
		while (left < right)
		{
			// 右边先走，找小
			while (left < right && a[right] >= a[keyi])
			{
				--right;
			}

			// 左边再走，找大
			while (left < right && a[left] <= a[keyi])
			{
				++left;
			}

			Swap(&a[left], &a[right]);
		}

		Swap(&a[left], &a[keyi]);
		keyi = left;

		// [begin, keyi-1]  keyi [keyi+1, end]
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
}

因为空间对效率的提示并不大，这里就不进行测试了，感兴趣的可以自己测一测

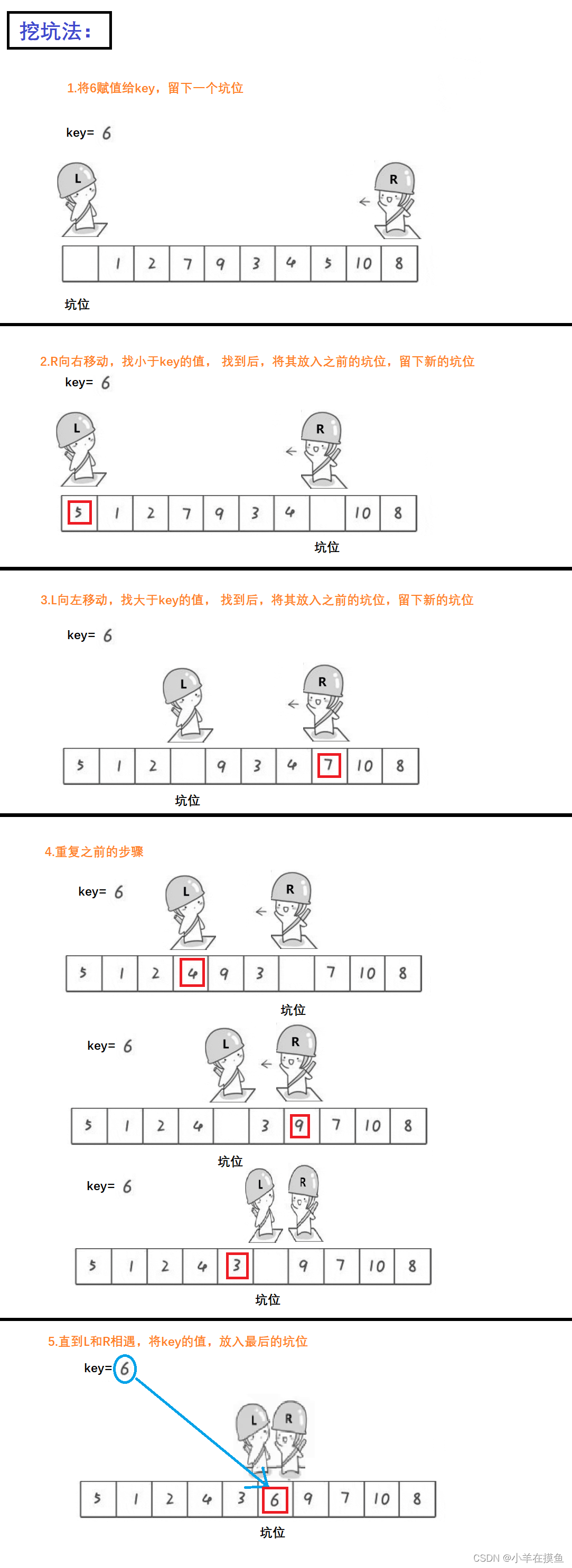
3. 挖坑法（快排的另一种思路）：

原理：

代码如下（递归实现）：

// 快速排序，挖坑法
void HoleQuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	//小区间优化
	if ((end - begin + 1) < 10)
	{
		// 小区间用直接插入替代，减少递归调用次数
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
		//三数选中间优化
		int mid = GetMidIndex(a, begin, end);
		Swap(&a[begin], &a[mid]);

		int left = begin, right = end;
		int key = a[left];
		int hole = left;
		while (left < right)
		{
			// 右边找小，填到左边坑里面
			while (left < right && a[right] >= key)
			{
				--right;
			}

			a[hole] = a[right];
			hole = right;

			// 左边找大，填到右边坑里面
			while (left < right && a[left] <= key)
			{
				++left;
			}

			a[hole] = a[left];
			hole = left;
		}

		a[hole] = key;

		// [begin, key-1]  key [key+1, end]
		QuickSort(a, begin, key - 1);
		QuickSort(a, key + 1, end);
	}
}

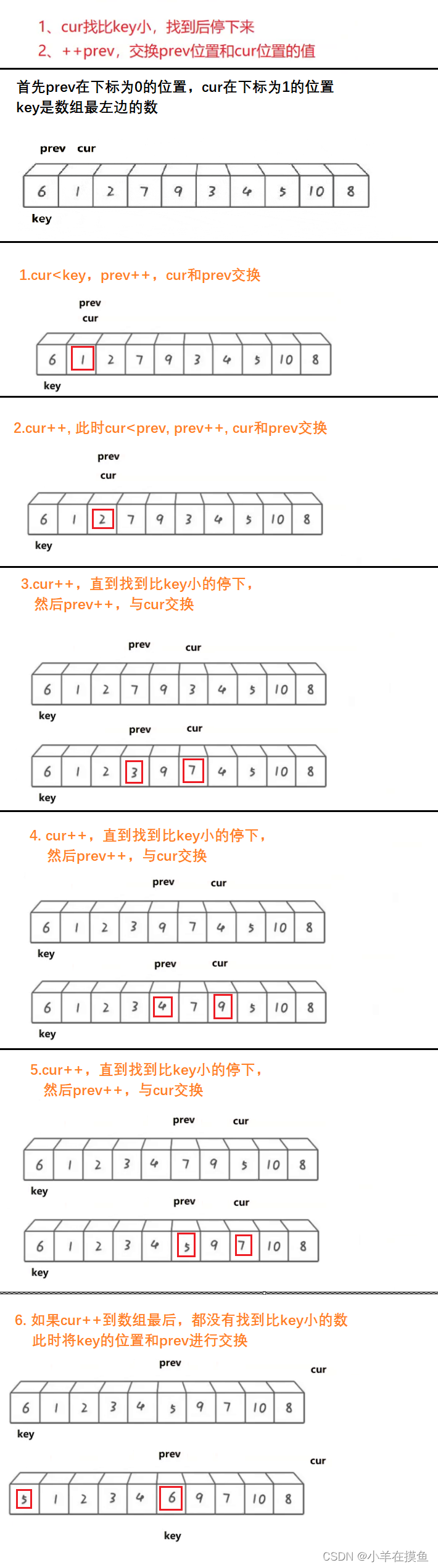
4. 快慢指针法（快排的第三种思路）：

 原理：

代码如下（递归实现）：

//快慢指针法
void PointQuickSort(int* a, int begin, int end)
{
	if (begin > end)
	{
		return;
	}
	
	//小区间优化
	if ((end - begin + 1) < 10)
	{
		// 小区间用直接插入替代，减少递归调用次数
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
		//三数选中间优化
		int mid = GetMidIndex(a, begin, end);
		Swap(&a[begin], &a[mid]);

		int prev = begin, cur = begin + 1;
		int key = prev;
		while (cur <= end)
		{
			while (cur <= end)
			{
				if (a[cur] >= a[key] && ++prev != cur)//++prev和cur的下标如果相等，就不要进行交换
				{
					Swap(&a[++prev], &a[cur]); //一定是先++prev，在用prev 
				}
				cur++;
			}
		}
		Swap(&a[prev], &a[key]);

		PointQuickSort(a, begin, key);
		PointQuickSort(a, key + 1, end);
	}
}

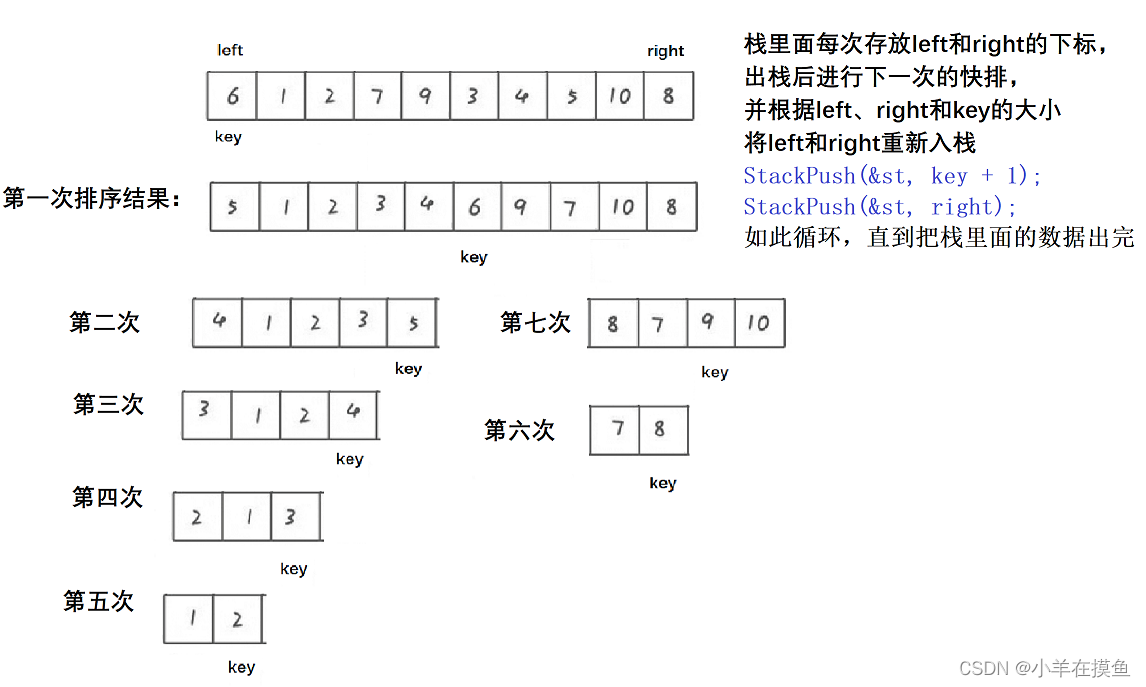
5.快速排序（非递归版代码）

非递归实现的方式有两种，一种是用栈实现，一种是用队列实现

用栈实现又叫做深度优先、用队列实现又叫做广度优先

原理如下：

基于栈的深度优先：

 

可以看出来，利用栈进行快排，是先左边的区间，后右边的区间，是往深的走，所以叫做深度优先

基于队列的广度优先：

基于队列的快排，是一层层的走的，和之前二叉树的层次遍历原理是相同的，因为是一层一层的走，所以叫做广度优先

代码如下（这里采用基于栈的深度优先）：

//快速排序（非递归）
//利用堆实现的叫做深度优先
void QuickSortNonR(int* a, int begin, int end)
{
	ST st;
	StackInit(&st);
	StackPush(&st, begin);
	StackPush(&st, end);

	while (!StackEmpty(&st))
	{
		int right = StackTop(&st);
		StackPop(&st);
		int left = StackTop(&st);
		StackPop(&st);

		//进行一次快排
		int prev = left, cur = left + 1;
		int key = left;
		while (cur <= right)
		{
            //++prev和cur的下标如果相等，就可以不用进行交换
			if (a[cur] < a[key] && ++prev != cur)
			{
				Swap(&a[prev], &a[cur]); 
			}
			cur++;
		}

		Swap(&a[prev], &a[key]);
		key = prev;

		// [left, key-1] keyi [key+1, right]
		if (key + 1 < right)
		{
			StackPush(&st, key + 1);
			StackPush(&st, right);
		}

		if (left < key - 1)
		{
			StackPush(&st, left);
			StackPush(&st, key - 1);
		}
	}

	StackDestroy(&st);
}

 

6.源代码（VS2022下编写）

#include "Stack.h" //引入了之前写的栈结构

#include<stdio.h>
#include<stdlib.h>
#include<time.h>



//声明：

//快速排序
void QuickSort(int* a, int begin, int end);
//三数取中
void MidQuickSort(int* a, int begin, int end);
//小空间优化
void SpaceQuickSort(int* a, int begin, int end);
//挖坑法
void HoleQuickSort(int* a, int begin, int end);
//快慢指针法
void PointQuickSort(int* a, int begin, int end);
//非递归法
void QuickSortNonR(int* a, int begin, int end);







//实现

//快速排序
void QuickSort(int* a, int begin, int end)
{
	//end -= 1;
	if (begin >= end)
	{
		return;
	}

	int left = begin, right = end;
	int key = left;
	while (left < right)
	{
		// 右边先走，找小
		while (left < right && a[right] >= a[key])
		{
			--right;
		}

		// 左边再走，找大
		while (left < right && a[left] <= a[key])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}

	Swap(&a[left], &a[key]);
	key = left;

	// [begin, keyi-1]  key [keyi+1, end]
	QuickSort(a, begin, key - 1);
	QuickSort(a, key + 1, end);
}
//快排改进：key选值的三数取中（优化时间）
int GetMidIndex(int* a, int begin, int end)
{
	int mid = (begin + end) / 2;
	if (a[begin] < a[mid])
	{
		if (a[mid] < a[end])
		{
			return mid;
		}
		else if (a[begin] > a[end])
		{
			return begin;
		}
		else
		{
			return end;
		}
	}
	else // a[begin] > a[mid]
	{
		if (a[mid] > a[end])
		{
			return mid;
		}
		else if (a[begin] < a[end])
		{
			return begin;
		}
		else
		{
			return end;
		}
	}
}
void MidQuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	int mid = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[mid]);

	int left = begin, right = end;
	int key = left;
	while (left < right)
	{
		// 右边先走，找小
		while (left < right && a[right] >= a[key])
		{
			--right;
		}

		// 左边再走，找大
		while (left < right && a[left] <= a[key])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}

	Swap(&a[left], &a[key]);
	key = left;

	// [begin, key-1]  key [key+1, end]
	QuickSort(a, begin, key - 1);
	QuickSort(a, key + 1, end);
}
//小区间优化（优化空间）
void SpaceQuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	if ((end - begin + 1) < 10)
	{
		// 小区间用直接插入替代，减少递归调用次数
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
		int mid = GetMidIndex(a, begin, end);
		Swap(&a[begin], &a[mid]);

		int left = begin, right = end;
		int keyi = left;
		while (left < right)
		{
			// 右边先走，找小
			while (left < right && a[right] >= a[keyi])
			{
				--right;
			}

			// 左边再走，找大
			while (left < right && a[left] <= a[keyi])
			{
				++left;
			}

			Swap(&a[left], &a[right]);
		}

		Swap(&a[left], &a[keyi]);
		keyi = left;

		// [begin, keyi-1]  keyi [keyi+1, end]
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
}
// 快速排序，挖坑法
void HoleQuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	//小区间优化
	if ((end - begin + 1) < 10)
	{
		// 小区间用直接插入替代，减少递归调用次数
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
		//三数选中间优化
		int mid = GetMidIndex(a, begin, end);
		Swap(&a[begin], &a[mid]);

		int left = begin, right = end;
		int key = a[left];
		int hole = left;
		while (left < right)
		{
			// 右边找小，填到左边坑里面
			while (left < right && a[right] >= key)
			{
				--right;
			}

			a[hole] = a[right];
			hole = right;

			// 左边找大，填到右边坑里面
			while (left < right && a[left] <= key)
			{
				++left;
			}

			a[hole] = a[left];
			hole = left;
		}

		a[hole] = key;

		// [begin, key-1]  key [key+1, end]
		QuickSort(a, begin, key - 1);
		QuickSort(a, key + 1, end);
	}
}
//快慢指针法
void PointQuickSort(int* a, int begin, int end)
{
	if (begin > end)
	{
		return;
	}
	
	//小区间优化
	if ((end - begin + 1) < 10)
	{
		// 小区间用直接插入替代，减少递归调用次数
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
		//三数选中间优化
		int mid = GetMidIndex(a, begin, end);
		Swap(&a[begin], &a[mid]);

		int prev = begin, cur = begin + 1;
		int key = prev;
		while (cur <= end)
		{
			if (a[cur] < a[key] && ++prev != cur)//++prev和cur的下标如果相等，就不要进行交换
			{
				Swap(&a[prev], &a[cur]); //一定是先++prev，在用prev 
			}
			cur++;
		}
		Swap(&a[prev], &a[key]);

		PointQuickSort(a, begin, key);
		PointQuickSort(a, key + 1, end);
	}
}

//快速排序（非递归）
//利用堆实现的叫做深度优先
void QuickSortNonR(int* a, int begin, int end)
{
	ST st;
	StackInit(&st);
	StackPush(&st, begin);
	StackPush(&st, end);

	while (!StackEmpty(&st))
	{
		int right = StackTop(&st);
		StackPop(&st);
		int left = StackTop(&st);
		StackPop(&st);

		//进行一次快排
		int prev = left, cur = left + 1;
		int key = left;
		while (cur <= right)
		{
			if (a[cur] < a[key] && ++prev != cur)//++prev和cur的下标如果相等，就不要进行交换
			{
				Swap(&a[prev], &a[cur]); 
			}
			cur++;
		}

		Swap(&a[prev], &a[key]);
		key = prev;

		// [left, key-1] keyi [key+1, right]
		if (key + 1 < right)
		{
			StackPush(&st, key + 1);
			StackPush(&st, right);
		}

		if (left < key - 1)
		{
			StackPush(&st, left);
			StackPush(&st, key - 1);
		}
	}

	StackDestroy(&st);
}









//主函数测试

void printArray(int* a, int n)
{
	for (int i = 0;i < n;i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

void TestInsertSort()
{
	int a[] = { 6,1,2,7,9,3,4,5,10,8 };
	//InsertSort(a, sizeof(a) / sizeof(int));
	//printArray(a, sizeof(a) / sizeof(int));

	//shellSort(a, sizeof(a) / sizeof(int));
	//printArray(a, sizeof(a) / sizeof(int));

	//HeapSort(a, sizeof(a) / sizeof(int));
	//printArray(a, sizeof(a) / sizeof(int));

	//BubbleSort(a, sizeof(a) / sizeof(int));
	//printArray(a, sizeof(a) / sizeof(int));

	//快排传的是：数组地址、开始下标、数组结尾下标
	HoleQuickSort(a, 0, sizeof(a) / sizeof(int) - 1);
	printArray(a, sizeof(a) / sizeof(int));

	QuickSortNonR(a, 0, sizeof(a) / sizeof(int)-1);
	printArray(a, sizeof(a) / sizeof(int));
}

void functionText()
{
	srand(time(0));
	const int N = 1000000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand() + i;
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a7[i];
	}

	//int begin1 = clock();
	//InsertSort(a1, N);
	//int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	//int begin3 = clock();
	//SelectSort(a3, N);
	//int end3 = clock();
	 
	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();
	
	/*int begin7 = clock();
	BubbleSort(a7, N);
	int end7 = clock();*/
	
	int begin5 = clock();
	MidQuickSort(a5, 0, N - 1);
	int end5 = clock();
	// 
	//int begin6 = clock();
	//MergeSort(a6, N);
	//int end6 = clock();

	printf("数据量为%d，以下时间单位为毫秒（ms）\n",N);
	//printf("InsertSort:	%d\n", end1 - begin1);
	printf("ShellSort:	%d\n", end2 - begin2);
	//printf("SelectSort:	%d\n", end3 - begin3);
	printf("HeapSort:	%d\n", end4 - begin4);
	//printf("BubbleSort:	%d\n", end7 - begin7);
	printf("QuickSort:	%d\n",end5 - begin5);
	//printf("MergeSort:%d\n", end6 - begin6);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}

int main()
{
	//TestInsertSort();

	//性能测试：
	functionText();

	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/423997.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Android Jetpack 从使用到源码深耕【调度任务组件WorkManager 从实践到原理 】（三）

Android Jetpack 从使用到源码深耕【调度任务组件WorkManager 从实践到原理 】（三）

本文，是Jetpack 调度任务组件WorkManager 从实践到原理系列文章的最后一篇，本文我们将对WorkManager 任务的具体执行源码，进行深入的解读。 大家坐好，我们要开始飙车了。 1.任务的具体执行 书接上文，我们既然知道了WorkManager，既然把worker包装为了workrequset，然后…
阅读更多...
本地生活为什么会迎来爆发？点赋科技带你了解这些关键点

本地生活为什么会迎来爆发？点赋科技带你了解这些关键点

随着全球疫情的结束和加速数字化转型进程&#xff0c;本地生活市场已经成为了经济发展的亮点。本地生活指的是人们在生活中所需的一切服务和消费&#xff0c;例如美食、购物、医疗保健、教育培训等各种类别。点赋科技就和大家来聊聊其中的一些关键点。 以下是本地生活迎来爆发的…
阅读更多...
网络编程套接字（ TCP ）

网络编程套接字（ TCP ）

目录 1、实现一个TCP网络程序&#xff08;单进程版&#xff09; 1.1、服务端serverTcp.cc文件 服务端创建套接字 服务端绑定 服务端监听 服务端获取连接 服务端提供服务 服务端main函数命令行参数 服务端serverTcp.cc总代码 1.2、客户端clientTcp.cc文件 客户端main函数命令行…
阅读更多...
【Java技术指南】「JPA编程专题」让你不再对JPA技术中的“持久化型注解”感到陌生了

【Java技术指南】「JPA编程专题」让你不再对JPA技术中的“持久化型注解”感到陌生了

JPA编程专题JPA的介绍JPA的介绍分析JPA注解总览JPA实体型注解EntityTableTableGeneratorTableGenerator 属性TemporalTransientColumnColumn 属性ColumnUniqueConstraint属性状态VersionVersionEmbeddable 和 EmbeddedEmbeddedEmbeddedIdMappedSuperclassEntityListenersEntity…
阅读更多...
30分钟Maven 从入门到精通

30分钟Maven 从入门到精通

一、什么是Maven Maven 是一个流行的 Java 项目构建和管理工具,它包含了一个项目对象模型 (POM Project Object Model) 一组标准集合。不仅简化了我们开发过程中对jar包依赖的导入&#xff0c;还对项目的清理、初始化、编译、测试、打包、集成测试、验证、部署和站点生成等所有…
阅读更多...
SpringCloud集成Seata saga模式案例

SpringCloud集成Seata saga模式案例

文章目录一、前言二、Seata saga模式介绍1、示例状态图2、“状态机”介绍1&#xff09;“状态机”属性2&#xff09;“状态”属性3&#xff09;更多状态相关内容三、SpringCloud 集成 seata saga1、saga模式状态机相关信息1&#xff09;状态机配置相关的三个表2&#xff09;状态…
阅读更多...
根据 cadence 设计图学习硬件知识 day01了解腾锐 D2000芯片

根据 cadence 设计图学习硬件知识 day01了解腾锐 D2000芯片

1. 首先了解 腾锐 D2000 1.介绍 腾锐D2000 芯片 D2000芯片集成8个飞腾自主研发的新一代高性能处理器内核FTC663&#xff0c;采用乱序四发射超标量流水线&#xff0c;兼容64位ARMV8指令集并支持ARM64和ARM32两种执行模式&#xff0c;支持单精度、双精度浮点运算指令和ASIMD处…
阅读更多...
ASP.NET动态Web开发技术第6章

ASP.NET动态Web开发技术第6章

第6章ASP.NET状态管理一.预习笔记 1.ASP.NET状态管理概述 状态管理是在一个网页或者不同网页的多个访问请求中&#xff0c;维护网页状态和信息的过程。 状态管理包含视图状态(ViewState)、控件状态(ControlState)、隐藏域状态(HiddenField)、Cookie、查询字符串(QueryString…
阅读更多...
24位AD和16位DA超高精度PID串级控制器在张力控制中的应用

24位AD和16位DA超高精度PID串级控制器在张力控制中的应用

摘要&#xff1a;针对目前张力控制器中普遍存在测量控制精度较差和无法实现串级控制这类高级复杂控制的问题&#xff0c;本文介绍了具有超高精度和多功能的新一代张力控制器。这种新一代张力控制器具有24位AD模数转换、16位DA数模转换、双精度浮点运算和0.01%的最小输出百分比&…
阅读更多...
【教程】使用R语言绘制词云图

【教程】使用R语言绘制词云图

哈喽&#xff0c;大家好&#xff0c;我是木易巷~ 最近木易巷在了解R语言&#xff0c;今天给大家分享一下使用R语言绘制出词云图的教程。 什么是R语言 R语言是一个开源的数据分析环境&#xff0c;起初是由数位统计学家建立起来&#xff0c;以更好的进行统计计算和绘图。由于R可…
阅读更多...
Android之AppWidget 开发浅析

Android之AppWidget 开发浅析

什么是AppWidget AppWidget 即桌面小部件&#xff0c;也叫桌面控件&#xff0c;就是能直接显示在Android系统桌面上的小程序&#xff0c;先看图&#xff1a; 图中我用黄色箭头指示的即为AppWidget&#xff0c;一些用户使用比较频繁的程序&#xff0c;可以做成AppWidget&#x…
阅读更多...
分布式系统概念和设计-分布式对象和远程调用

分布式系统概念和设计-分布式对象和远程调用

分布式系统概念和设计 分布式对象和远程调用 能够接收远程方法调用的对象称为远程对象&#xff0c;远程对象实现一个远程接口。 调用者和被调用对象分别存在不同的失败可能性&#xff0c;RMI和本地调用有不同的语义。 中间件 在进程和消息传递等基本构造模块之上提供编程模型的…
阅读更多...
PDCA循环模型——如何用同样的时间做更多的事？【No.1 】

PDCA循环模型——如何用同样的时间做更多的事？【No.1 】

PDCA循环模型&#xff0c;又称戴明环&#xff0c;是一个持续改进模型。PDCA循环包括以下内容&#xff1a; Plan阶段&#xff1a;确认目标&#xff0c;制定计划Do阶段&#xff1a;执行措施和计划Check阶段&#xff1a;检查验证&#xff0c;评估效果Action阶段&#xff1a;有效措…
阅读更多...
健哥MYSQL私房菜 - 基础与介绍

健哥MYSQL私房菜 - 基础与介绍

前言 从今天开始, 健哥就带各位小伙伴学习数据库技术。数据库技术是Java开发中必不可少的一部分知识内容。也是非常重要的技术。本系列教程由浅入深, 全面讲解数据库体系。 非常适合零基础的小伙伴来学习。 ------------------------------前戏已做完&#xff0c;精彩即开始---…
阅读更多...
docker-compose详讲

docker-compose详讲

一、概述 docker-compose 项目是docker官方的开源项目&#xff0c; 负责实现对docker容器集群的快速编排&#xff0c;来轻松高效的管理容器&#xff0c;定义运行多个容器。 docker-compose将所管理的容器分为三层&#xff0c; 分别是工程&#xff08;project&#xff09;&#…
阅读更多...
C#，码海拾贝（19）——一般实矩阵的QR分解（QR Decomposition）方法之C#源代码，《C#数值计算算法编程》源代码升级改进版

C#，码海拾贝（19）——一般实矩阵的QR分解（QR Decomposition）方法之C#源代码，《C#数值计算算法编程》源代码升级改进版

1 实矩阵 实矩阵&#xff0c;指的是矩阵中所有的数都是实数的矩阵。如果一个矩阵中含有除实数以外的数&#xff0c;那么这个矩阵就不是实矩阵。 2 QR&#xff08;正交三角&#xff09;分解法 QR&#xff08;正交三角&#xff09;分解法是求一般矩阵全部特征值的最有效并广泛应…
阅读更多...
基于Java+SpringBoot制作一个宿舍报修小程序

基于Java+SpringBoot制作一个宿舍报修小程序

制作一个宿舍报修小程序&#xff0c;让学生实现快速报修&#xff0c;将流程进行精简&#xff0c; 便于管理部门有效响应。 微信小程序实战开发专栏 一、小程序1.1 项目创建1.2 首页iconfont图标引入1.3 报修管理报修提交报修记录报修溯源1.4 来访登记1.5 公告通知二、API2.1 Sp…
阅读更多...
windows日志捕获工具-DebugView使用教程

windows日志捕获工具-DebugView使用教程

debugview 是一款捕获windows桌面系统程序中由TRACE(debug版本)和OutputDebugString输出的信息。 1、双击打开DebugView.exe工具&#xff0c;看到如下界面&#xff1a; 其中这里 Include代表过滤想要的关键字&#xff0c;一般不会找自己想要的关键字日志就设置成星号*&#xf…
阅读更多...
GDOUCTF WEB

GDOUCTF WEB

web hate eat snake 游戏题找js&#xff0c;将判断语句删掉即可 ezweb 看源码找到/src路由&#xff0c;找到源码 import flaskapp flask.Flask(__name__)app.route(/, methods[GET]) def index():return flask.send_file(index.html)app.route(/src, methods[GET]) def so…
阅读更多...
如何快速开发软件？这篇文章说明白了

如何快速开发软件？这篇文章说明白了

随着经济迅速发展&#xff0c;传统软件开发模式存在研发周期长、需求转化困难、投入成本高等问题&#xff0c;无法适应当前业务发展速度,市场需要快速开发工具。快速开发软件可分为代码生成类、少代码类、零代码功能配置类。代码生成类相对灵活&#xff0c;但对用户要求高&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023