本文默认卷积的输入输出数据格式为NHWC。

1x1卷积

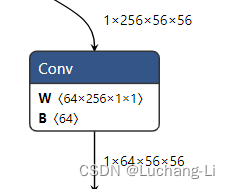
输入shape为[N, H, W, C] , filter为[Hf, Wf, Ci, Co]

FH, FW都为1，直接把输入shape reshape为[N, H * W, C], filter reshape为[[Hf * Wf * Ci, Co],然后进行矩阵乘得到[N, H * W, Co]，再reshape为卷积的output shape即可。

kernel shape=strides卷积

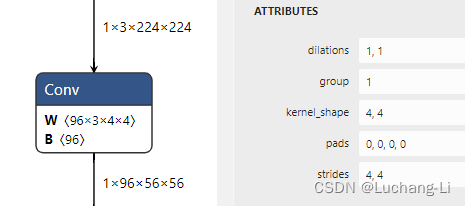
跟1x1卷积类似，这种卷积特点是每次卷积计算的输入数据块之间没有重叠，可以结合transpose简单处理为矩阵乘：

假设输入格式为[N, H, W, C]，可以重新解释为[N, H1*H0, W1*W0, C], H0,W0即为kernel_shape大小，H1和W1为卷积输出的图像宽度，而filter的格式为[Hf, Wf, Ci, Co]

把卷积输入从[N, H1*H0, W1*W0, C] reshape和transpose转换为[N,H1*W1,H0*W0*C]，然后与filter的[Hf*Wf*Ci, Co]做矩阵乘即可，得到输出为[N, Ho*Wo, Co]，reshape为卷积输出的shape即可。

显式矩阵乘卷积（explicit GEMM convolution）

也叫做Im2Col或者im2row。这需要把卷积拆分为Im2Col和矩阵乘两个算子。

Im2Col思想非常简单，也就是把输入每次filter覆盖的FH*FW*Ci的那部分数据展开成为一行，作为矩阵乘的K，而filter的Co作为矩阵乘的N。

而输入数据整个Hi*Wi的图像宽度要计算Ho*Wo次卷积计算，因此作为矩阵乘的M部分，因此，输入数据经过Im2Col后变成[N, Ho*Wo, FH*FW*Ci]的tensor，而卷积的filter reshape为[FH*FW*Ci, Co]的tensor，两个做矩阵乘得到[N, Ho*Wo, Co]，再Reshape一下即可作为卷积的输出。

这个方法的一个巨大的缺点是Im2Col之后的临时数据相比卷积的输入有巨大的提升，导致会占用大量的内存，特别是stride=1的情况。比如kernel_shape为3x3，stride=1，那么Im2Col后的张量数据为卷积输入的9倍。

隐式矩阵乘卷积（implicit GEMM convolution）

与Im2Col方法一样，但是不需要把卷积拆分为两个独立的Im2Col和矩阵乘两个部分，而是在矩阵乘计算的数据读取时，采用特定的数据读取方法，实现im2col。

implicit GEMM方法更偏好输入数据格式为NC1HWC0， 其中输入的C=C1*C0，C0通常为4,8,16等。

具体计算方法参考

卷积：从推理引擎优化和硬件优化角度理解 - 知乎

The Indirect Convolution Algorithm

Winograd卷积

这种方法虽然只能处理几种比较特定kernel shape和stride的场景，但性能通常比Im2Col方法更好。Winograd通过input 和weight transform把卷积转换为矩阵乘计算，最后再通过output transform得到卷积结果，具体原理参考：

Winograd算法实现卷积原理_winograd卷积_Luchang-Li的博客-CSDN博客

winograd卷积实践_Luchang-Li的博客-CSDN博客

Ref

卷积：从推理引擎优化和硬件优化角度理解 - 知乎

OpenPPL 中的卷积优化技巧 - 知乎

The Indirect Convolution Algorithm