---

生存函数（Survival function）是一个函数，它给出了患者、设备或其他感兴趣的对象在特定时间后存活的概率。生存函数也称为幸存者函数（survivor function）或可靠性函数（reliability function）。可靠性函数在工程中很常见，而生存函数用于更广泛的应用，包括人类死亡率。生存函数是生命周期的互补累积分布函数（complementary cumulative distribution function）。有时互补的累积分布函数被统称为生存函数。

1. 定义

设生命周期 $T$ 为区间 $[0,\infty )$ 上具有累积分布函数 $F(t)$ 和概率密度函数 $f(t)$ 的连续随机变量。其生存函数或可靠性函数为：

S ( t ) = P ( { T > t } ) = ∫ t ∞ f ( u )   d u = 1 − F ( t ) S(t)=P(\{T>t\})=\int _{t}^{\infty }f(u)\,\mathrm{d}u=1-F(t) S(t)=P({T>t})=∫t∞​f(u)du=1−F(t)

2. 生存函数的例子

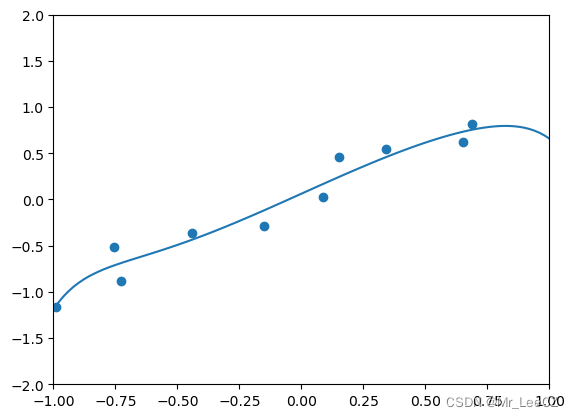
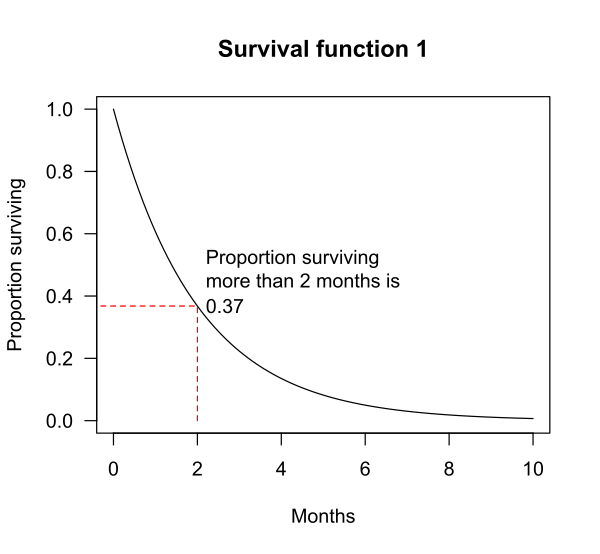
下图显示了假设生存函数的示例。$x$ 轴是时间。$y$ 轴是受试者存活的比例。这些图表显示了受试者在时间 $t$ 之后存活的概率。

图 四种生存函数

例如，对于生存函数 1，生存时间超过 $t=2$ 个月的概率为 0.37。也就是说，37% 的受试者存活超过 2 个月。

图 生存函数 1

对于生存函数 2，生存时间超过 $t=2$ 个月的概率为 0.97。也就是说，97% 的受试者存活超过 2 个月。

图 生存函数 2

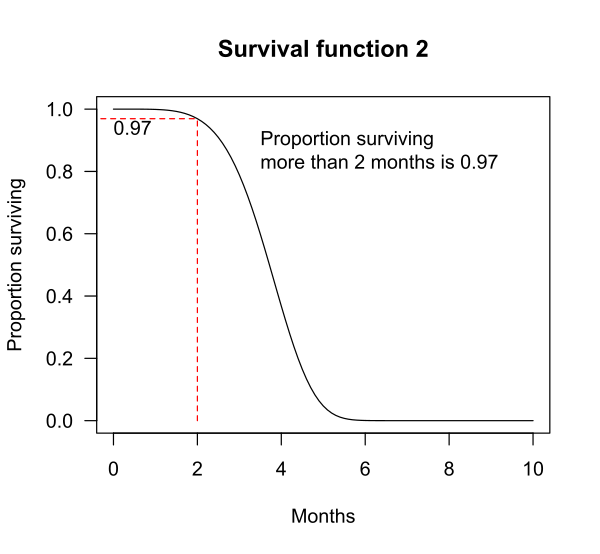
中位生存期（Median survival）可由生存函数确定。例如，对于生存函数 2，50% 的受试者存活了 3.72 个月。 因此，中位生存期为 3.72 个月。

图 生存函数中位生存期

在某些情况下，无法从图中确定中位生存期。例如，对于生存函数 4，超过 50% 的受试者生存时间超过 10 个月的观察期。

图 中位生存期大于 10 个月

生存函数是描述和显示生存数据的几种方法之一。显示数据的另一种有用方法是显示受试者生存时间分布的图表。 Olkin，第 426 页给出了以下生存数据示例。 记录空调系统连续故障之间的小时数。连续失败之间的时间为 1、3、5、7、11、11、11、12、14、14、14、16、16、20、21、23、42、47、52、62、71、71、 87、90、95、120、120、225、246 和 261 小时。平均故障间隔时间为 59.6。 该平均值将很快用于将理论曲线拟合到数据。下图显示了故障间隔时间的分布。图表下方的蓝色刻度线是连续失败之间的实际小时数。

图 交流故障次数分布

故障时间的分布覆盖有表示指数分布的曲线。对于此示例，指数分布近似于故障时间的分布。指数曲线是适合实际故障时间的理论分布。这个特定的指数曲线由参数 lambda 指定，$\lambda =1/(\text{平均无故障时间})=1/59.6=0.0168$。如果时间可以取任何正值，则故障时间的分布称为概率密度函数（pdf）。在方程式中，pdf 指定为 $f(t)$。如果时间只能取离散值（如 1 天、2 天等），则失效时间的分布称为概率质量函数（pmf）。大多数生存分析方法都假设时间可以取任何正值，$f(t)$ 是 pdf。如果使用指数函数近似观察到的空调故障之间的时间，则指数曲线给出空调故障次数的概率密度函数 $f(t)$。

显示生存数据的另一种有用方法是显示每个时间点的累积故障的图表。这些数据可以显示为累计次数，也可以显示为每次失败的累计比例。下图显示了空调系统每次发生故障的累积概率（或比例）。黑色阶梯线显示失败的累积比例。对于每个步骤，图表底部都有一个蓝色勾号，表示观察到的故障时间。 平滑的红线表示拟合观测数据的指数曲线。

到每个时间点的累积故障概率图称为累积分布函数（cumulative distribution function）或 CDF。 在生存分析中，累积分布函数给出生存时间小于或等于特定时间 $t$ 的概率。

令 $T$ 为生存时间，它是任何正数。特定时间由小写字母 $t$ 指定。$T$ 的累积分布函数是函数：

$$F(t)=P(T\le t)$$

其中右侧表示随机变量 $T$ 小于或等于 $t$ 的概率。如果时间可以取任意正值，则累积分布函数 $F(t)$ 是概率密度函数 $f(t)$ 的积分。

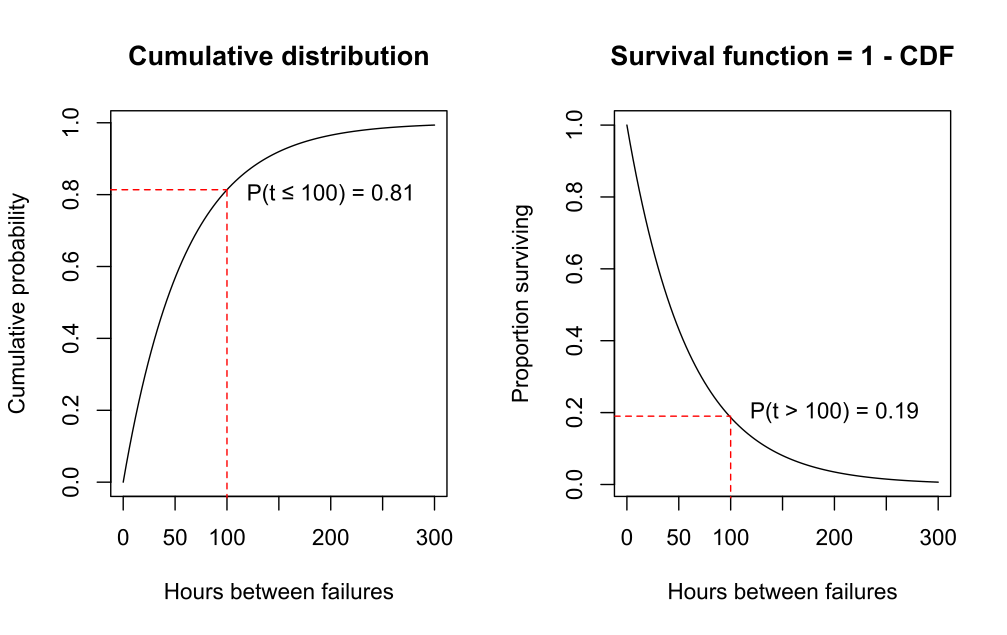
对于空调示例，下面的 CDF 图表说明了故障时间小于或等于 100 小时的概率为 0.81，这是使用数据拟合的指数曲线估算的。

图 AC 无故障时间 LT 100 小时

绘制故障时间小于或等于 100 小时的概率的替代方法是绘制故障时间大于 100 小时的概率。故障时间大于 100 小时的概率必须为 1 减去故障时间小于或等于 100 小时的概率，因为总概率总和必须为 1。

这给出了：

$$P(\text{failure time}>100\text{hours})=1-P(\text{failure time}<100\text{hours})=1–0.81=0.19$$

此关系推广到所有故障时间：

$$P(T>t)=1-P(T<t)=1–\text{cumulative distribution function}$$

这种关系如下图所示。左图是累积分布函数，即 $P(T<t)$。右图为 $P(T>t)=1-P(T<t)$。右图是生存函数 $S(t)$。$S(t)=1–\text{CDF}$ 这一事实是生存函数的另一个名称是互补累积分布函数的原因。

图 生存函数为 1 - CDF

3. 参数生存函数

在某些情况下，例如空调的例子，生存时间的分布可以用指数分布等函数很好地近似。几种分布常用于生存分析，包括指数分布、威布尔分布、伽玛分布、正态分布、对数正态分布和对数逻辑分布。这些分布由参数定义。例如，正态（高斯）分布由两个参数均值和标准差定义。由参数定义的生存函数被称为参数化的（parametric）。

在上面显示的四个生存函数图中，生存函数的形状由特定的概率分布定义：生存函数 1 由指数分布定义，2 由威布尔分布（Weibull distribution）定义，3 由对数逻辑分布（log-logistic distribution）定义 , 4 由另一个 Weibull 分布定义。

3.1 指数生存函数（Exponential survival function）

对于指数生存分布，无论个人或设备的年龄如何，每个时间间隔的失败概率都是相同的。这一事实导致了指数生存分布的“无记忆”特性：受试者的年龄对下一个时间间隔内的失败概率没有影响。指数可能是系统生命周期的一个很好的模型，其中部件在故障时被更换。它也可用于模拟短时间内活生物体的生存。它不太可能成为生物体完整生命周期的良好模型。正如 Efron 和 Hastie （第 134 页）指出的那样，“如果人类的寿命是指数级的，那么就不会有老人或年轻人，只有幸运者或不幸者”。

3.2 威布尔生存函数（Weibull survival function）

指数生存函数的一个关键假设是风险率是常数。在上面给出的例子中，每年死亡的男性比例恒定为 10%，这意味着危险率是恒定的。持续危险的假设可能不合适。例如，在大多数生物体中，老年死亡的风险大于中年——也就是说，危险率随着时间的推移而增加。对于某些疾病，例如乳腺癌，5 年后复发的风险较低——也就是说，风险率随时间降低。Weibull 分布扩展了指数分布以允许恒定的、增加的或减少的危险率。

3.3 其他参数生存函数

还有其他几个参数生存函数可以更好地拟合特定数据集，包括正态、对数正态、对数逻辑和伽玛。可以使用图形方法或使用正式的拟合检验来为特定应用选择参数分布。这些分布和测试在生存分析教科书中有描述。Lawless 广泛涵盖了参数模型。

参数化生存函数通常用于制造应用中，部分原因是它们能够估计观察期以外的生存函数。然而，参数函数的适当使用要求数据通过所选分布很好地建模。如果没有合适的分布，或者无法在临床试验或实验之前指定，则非参数生存函数提供了一个有用的替代方案。

4. 非参数生存函数

生存的参数模型可能是不可能的或不可取的。在这些情况下，对生存函数建模的最常用方法是非参数 Kaplan–Meier 估计器（Kaplan–Meier estimator）。

5. 性质

• 每个生存函数 $S(t)$ 单调递减，即对所有 $u>t$，$S(u)\le S(t)$。
  • 它是随机变量的一个属性，它将一组事件映射到时间上，这些事件通常与某些系统的死亡率或故障相关。
• 时间 $t=0$ 时，代表某个起源，通常是研究的开始或某个系统运行的开始。$S(0)$ 通常是统一的，但可以更小以表示系统在运行时立即失败的概率。
• 由于 CDF 是右连续函数，因此生存函数 $S(t)=1-F(t)$ 也是右连续的。
• 生存函数可以和概率密度函数 $f(t)$ 还有风险函数（hazard function）$\lambda (t)$ 相关联：

$$f(t)=-S^{\prime }(t)$$
$$\lambda (t)=-\frac{\mathrm{d}}{\mathrm{d}t}\log S(t)$$

所以：

$$S(t)=\exp [-{\int }_0^t\lambda (t^{\prime })\mathrm{d}{t}^{\prime }]$$

• 预期生存时间：

$$\mathbb{E}(T)={\int }_0^{\infty }S(t)\mathrm{d}t$$

6. Kaplan–Meier estimator

Kaplan–Meier 估计器（Kaplan–Meier estimator），也称为乘积极限估计器（product limit estimator），是一种非参数统计量（non-parametric statistic），用于根据生命周期数据估计生存函数。在医学研究中，常用于衡量患者在治疗后存活一定时间的比例。在其他领域，Kaplan-Meier 估计量可用于衡量人们在失业后保持失业状态的时间长度，机器部件的故障时间，或植物上的肉质果实在由食肉动物被移除之前保留了多长时间 。该估算器以 Edward L. Kaplan 和 Paul Meier 的名字命名，他们各自向美国统计协会杂志提交了类似的手稿。期刊编辑 John Tukey 说服他们将他们的工作合并成一篇论文，该论文自 1958 年发表以来已被引用超过 61,800 次。

生存函数 $S(t)$ 的估计量（寿命长于 $t$）由下式给出：

$$\hat{S}(t)=\prod _{i:t_i\le t}\left(1-\frac{d_i}{n_i}\right)$$

$t_i$ 为至少有一个事件发生的时间，$d_i$ 为在该时间 $t_i$ 发生的事件（例如，死亡）的数量，$n_i$ 为到时间 $t_i$ 为止已知的幸存者（尚未发生事件或被审查）。

6.1 基本概念

Kaplan–Meier 估计量的图是一系列递减的水平步长，在样本量足够大的情况下，接近该人群的真实生存函数。假设连续不同采样观察值（“点击（click）”）之间的生存函数值是常数。

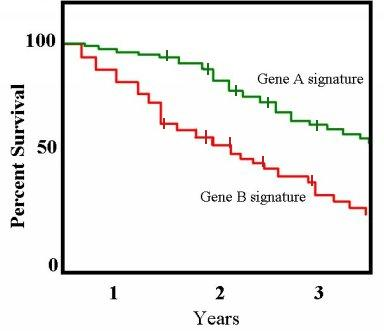
Kaplan-Meier 曲线的一个重要优点是该方法可以考虑某些类型的删失数据（censored data），特别是右删失（right-censoring），如果患者退出研究，失去随访，或在最后一次随访中没有事件发生。在图上，小的垂直刻度线表示存活时间已被右删失的个体患者。当没有截断或删失发生时，Kaplan-Meier 曲线是经验分布函数（empirical distribution function）的补集。

在医学统计中，一个典型的应用程序可能涉及将患者分组，例如，具有基因 A 概况的患者和具有基因 B 概况的患者。在图中，基因 B 的患者比基因 A 的患者死得更快。两年后，大约 80% 的基因 A 患者存活下来，但只有不到一半的基因 B 患者存活下来。

要生成 Kaplan-Meier 估计量，每个患者（或每个受试者）至少需要两条数据：最后一次观察的状态（事件发生或右删失）和事件发生时间（或删失时间）。如果要比较两个或多个组之间的生存函数，则需要第三个数据：每个受试者的组分配（group assignment）。

7. 比例风险模型（Proportional hazards model）

比例风险模型是统计学中的一类生存模型。生存模型将某个事件发生之前经过的时间与可能与该时间量相关联的一个或多个协变量（covariates）相关联。在比例风险模型中，协变量中单位增加的独特效应相对于风险率是乘法的。例如，服用一种药物可能会使一个人发生中风的危险率减半，或者，改变制造部件的制造材料可能会使其发生故障的危险率增加一倍。其他类型的生存模型（例如加速故障时间模型（accelerated failure time models））不会出现比例风险。加速故障时间模型描述了事件的生物或机械生命历史加速（或减速）的情况。

图 与患者生存相关的两种情况的 Kaplan-Meier 图示例。

7.1 背景

生存模型可以被视为由两部分组成：潜在的基线风险函数（underlying baseline hazard function），通常表示为 ${\lambda }_0(t)$，描述在协变量的基线水平下，每个时间单位的事件风险如何随时间变化；和影响参数（effect parameters），描述危害如何响应解释性协变量（explanatory covariates）而变化。一个典型的医学示例将包括分配疗法等协变量，以及研究开始时的年龄、性别和研究开始时是否存在其他疾病等患者特征，以减少变异性和/或控制混杂。

比例风险条件指出协变量与风险呈乘法关系。例如，在最简单的固定系数情况下，药物治疗可能会在任何给定时间 $t$ 将受试者的危险减半，而基线危害可能会有所不同。但是请注意，这不会使对象的寿命加倍；协变量对寿命的精确影响取决于 ${\lambda }_0(t)$。协变量不限于二元预测变量（binary predictors）； 在连续协变量 $x$ 的情况下，通常假设危害呈指数反应；每增加一个单位 $x$ 导致危险按比例缩放。

7.2 问题定义

让 $\tau \ge 0$ 是一个随机变量，我们将其视为感兴趣事件发生之前的时间。如上所述，目标是估计在 $\tau$ 下的生存函数 $S$。这个函数被定义为：

$$S(t)=\mathrm{Prob}(\tau >t)，\text{where}t=0,1,\dots \text{is the time}$$

让 ${\tau }_1,\dots ,{\tau }_n\ge 0$ 是独立同分布的随机变量，其公共分布（common distribution）是 $\tau$：${\tau }_j$ 是某个事件 $j$ 发生时的随机时间。可用于估计 $S$ 的数据不是 $({\tau }_j{)}_{j=1,\dots ,n}$，而是一系列的对 $(({\tilde{\tau }}_j,c_j){)}_{j=1,\dots ,n}$，其中 j ∈ [ n ] : = { 1 , 2 , … , n } j\in [n]:=\{1,2,\dots ,n\} j∈[n]:={1,2,…,n}，$c_j\ge 0$ 是一个固定的确定性整数，事件 $j$ 的结尾时间（censoring time）和 ${\tilde{\tau }}_j=\min ({\tau }_j,c_j)$。特别是有关事件 $j$ 发生时间的可用信息是事件是否在固定时间 $c_j$ 之前发生。如果是，那么事件的实际时间也是可用的。挑战在于给定此数据估计 $S(t)$。

7.3 The Cox model

7.3.1 介绍

David Cox 爵士观察到，如果比例风险假设成立（或假设成立），则可以估计影响参数（effect parameter），表示为 ${\beta }_i$。下面，没有考虑完整的危险函数。这种生存数据方法称为 Cox 比例风险模型（Cox proportional hazards model）的应用，有时缩写为 Cox 模型（Cox model）或比例风险模型（proportional hazards model）。然而，Cox 还指出，比例风险假设的生物学解释可能非常棘手。

令 $X_i=(X_{i1},\cdots ,X_{ip})$ 为受试者 $i$ 的协变量的实际值。Cox 比例风险模型的风险函数具有以下形式：

$$\begin{array}{rl}\lambda (t|X_i)& ={\lambda }_0(t)\exp ({\beta }_1{X}_{i1}+\cdots +{\beta }_p{X}_{ip})\\ & ={\lambda }_0(t)\exp (X_i\cdot \beta )\end{array}$$

该表达式给出了对象 $i$ 在时间 $t$ 的风险函数，协变量向量（解释变量（explanatory variables））$X_i$。请注意，在受试者之间，基线风险 ${\lambda }_0(t)$ 是相同的（不依赖于 $i$）。受试者风险之间的唯一区别来自基线比例因子 $\exp (X_i\cdot \beta )$。

---

• 参考文献

wiki: Survival function

wiki: Kaplan–Meier estimator

wiki: Proportional hazards model