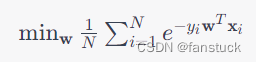不可导凸函数的最优解搜索问题

1. 次梯度下降方法

如目标函数包含不可微分的部分，形如
$$E(\mathbf{w})=\frac{1}{N}\Vert \mathbf{y}-\hat{\mathbf{y}}(\mathbf{w}){\Vert }_2^2+\lambda \cdot \Vert \mathbf{w}{\Vert }_1$$

其最优解则无法使用经典的梯度下降法进行求解。我们需要引入次梯度的概念

次梯度：设$F:{\mathbb{R}}^n\to \mathbb{R}$ 为一个$n$元函数，如果 $\mathbf{g},\mathbf{w}\in {\mathbb{R}}^n$ 满足如下性质：
$$F(\mathbf{u})\ge F(\mathbf{w})+⟨\mathbf{g},\mathbf{u}-\mathbf{w}⟩\forall \mathbf{u}\in {\mathbb{R}}^n$$
则称 $\mathbf{g}$ 是 $F$ 在 $$\mathbf{w}$ 处的次梯度。称集合 ∂ F ( u ) = { g ∈ R n : g 为 F 在 w 处的次梯度 } \partial F(\boldsymbol{u})=\{\boldsymbol{g}\in\mathbb{R}^n:\boldsymbol{g}为F在\boldsymbol{w}处的次梯度\} ∂F(u)={g∈Rn:g为F在w处的次梯度} 为 $F$ 在 $\mathbf{w}$ 处的次梯度.

例：求目标函数 $F(\mathbf{w})=\Vert \mathbf{w}{\Vert }_1$ 的次梯度。
解：由于 $F(\mathbf{w})=\Vert \mathbf{w}{\Vert }_1=|x_1|+|x_2|+\cdots +|x_d|$，对任意的分量 $F(w)=|w|$, 则有
$$F(u)\ge F(0)+g\cdot (u-0)$$
即
$$|u|\ge |0|+g\cdot (u-0)$$
则
$$-1\le g\le 1$$
综上
$$\partial F(w)=\{\begin{array}{r}-1x<0\\ [-1,1]x=0\\ 1x>0\end{array}$$

注意：由于次梯度是一个集合，编程实现时我们只需要取其中一个值即可。
则$$\partial \Vert \mathbf{w}{\Vert }_1=sign(\mathbf{w})=\{\begin{array}{r}-1\mathbf{w}<0\\ 0\mathbf{w}=0\\ 1\mathbf{w}>0\end{array}$$

1.1 基于次梯度的 Lasso 回归求解

Lasso 回归的目标函数为

$$F(\mathbf{w})=\frac{1}{n}\Vert \mathbf{Xw}-\mathbf{y}{\Vert }_2^2+\lambda \cdot \Vert \mathbf{w}{\Vert }_1$$

次梯度为

$$\frac{2}{n}{\mathbf{X}}^{\top }(\mathbf{Xw}-\mathbf{y})+\lambda \cdot \text{sign}(\mathbf{w})\in \partial F(\mathbf{w})$$

其中

$$\text{sign}(\mathbf{w})=\{\begin{array}{r}-1\mathbf{w}<0\\ 0\mathbf{w}=0\\ 1\mathbf{w}>0\end{array}$$

1.2 次梯度求解 Lasso 算法

算法 1: 基于次梯度的lasso回归算法
输入: $X$, $\mathbf{y}$
1:      \;\; $\mathbf{w}=0$
2:      \;\; for $t=1,2,\cdots ,N$：
3: $\mathbf{e}=2X^T(X\mathbf{w}-\mathbf{y})/n+sign(\mathbf{w})$ ;
4: $\mathbf{w}=\mathbf{w}-\alpha \cdot \mathbf{e}$ ;
5: \qquad 转入step 3;
输出: $\mathbf{w}$

1.3 编程实现

# 基于次梯度的lasso回归最优解
# 输入：
#     X：m*d维矩阵（其中第一列为全1向量，代表常数项），每一行为一个样本点，维数为d
#     y: m维向量
# 参数：
#     Lambda: 折中参数
#     eta:次梯度下降的步长
#     maxIter: 梯度下降法最大迭代步数
# 返回：
#    weight：回归方程的系数
class LASSO_SUBGRAD:
    def __init__(self, Lambda=1,eta=0.1, maxIter=1000):
        self.Lambda = Lambda
        self.eta = eta
        self.maxIter = maxIter

    def fit(self, X, y):
        n,d = X.shape
        w = np.zeros((d,1)) 
        self.w = w
        for t in range(self.maxIter):
            e = X@w - y
            v = 2 * X.T@e / n + self.Lambda * np.sign(w)
            w = w - self.eta * v  
            self.w += w
        self.w /= self.maxIter
        return 
    
    def predict(self, X):
        return X@self.w

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt

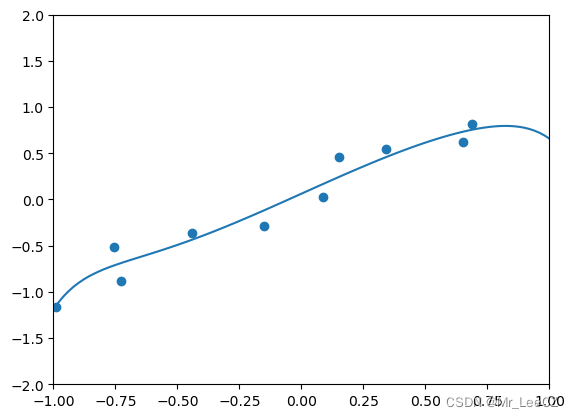
def generate_samples(m):
    X = 2 * (np.random.rand(m, 1) - 0.5) 
    y = X + np.random.normal(0, 0.3, (m,1))
    return X, y

np.random.seed(100)
X, y = generate_samples(10)
poly = PolynomialFeatures(degree = 10)
X_poly = poly.fit_transform(X)
model = LASSO_SUBGRAD(Lambda=0.001, eta=0.01, maxIter=50000)
model.fit(X_poly, y)

plt.axis([-1, 1, -2, 2])
plt.scatter(X, y)
W = np.linspace(-1, 1, 100).reshape(100, 1)
W_poly = poly.fit_transform(W)
u = model.predict(W_poly)
plt.plot(W, u)
plt.show()

import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

def process_features(X):
    scaler = StandardScaler()
    X = scaler.fit_transform(X)
    m, n = X.shape
    X = np.c_[np.ones((m, 1)), X]  
    return X
    
housing = fetch_california_housing()
X = housing.data  
y = housing.target.reshape(-1,1)  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
X_train = process_features(X_train)
X_test = process_features(X_test)

model = LASSO_SUBGRAD(Lambda=0.1)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
score = r2_score(y_test, y_pred)
print("mse = {}, r2 = {}".format(mse, score))

2. 软阈值方法

目标函数
$$\mathcal{L}\left(\mathbf{x}\right)=\frac{1}{2}{\Vert \mathbf{x}-\mathbf{b}\Vert }_2^2+\gamma {\Vert \mathbf{x}\Vert }_1$$
存在问题：不可微分。

策略：转化成分量，即解藕成几个分量的和
$$\mathcal{L}\left(\mathbf{x}\right)=\left\{\frac{1}{2}(x_1-b_1{)}^2+\gamma \left|x_1\right|\right\}+\left\{\frac{1}{2}(x_2-b_2{)}^2+\gamma \left|x_2\right|\right\}+\cdots +\left\{\frac{1}{2}(x_n-b_n{)}^2+\gamma \left|x_n\right|\right\}$$
每个独立的部门均是同一个优化问题
$$Q(x)=\frac{1}{2}(x-b{)}^2+\gamma \left|x\right|x,b\in R$$
对上式关于$x$求导得：
$$\frac{\partial Q(x)}{\partial x}=x-b+\gamma \cdot sign(x)=0$$
则有
$$x=b-\gamma \cdot sign(x)=0\cdots (6)$$
公式（6）中的解$x$与其符号有很大关系需讨论

（i）当$x>0$时，$x=b-\gamma >0$，同时需要$b>\Gamma$

$\bullet$当$b<-\Gamma$时，$x=b+\Gamma$；

$\bullet$当$-\Gamma \le b\le 0$时，$x$无极点（$x>0$），$x=0$为目标函数最大值。

综上可知
$$\hat{x}=S_{\gamma }(b)=\{\begin{array}{cc}b-\gamma & b>\gamma \\ 0& -\gamma \le b\le \gamma \\ b+\gamma & b<-\gamma \end{array}$$
或
x ^ = S γ ( b ) = s i g n ( b ) ⋅ m a x { ∣ b ∣ − γ , 0 } \hat{x} =S_\gamma(b)=sign(b)·max\left \{ \left | b \right | -\gamma,0 \right \} x^=Sγ​(b)=sign(b)⋅max{∣b∣−γ,0}

2.1 软阈值求解Lasso回归

# 基于软阈值法的lasso回归最优解（ADMM）
# 输入：
#     X：m*d维矩阵（其中第一列为全1向量，代表常数项），每一行为一个样本点，维数为d
#     y: m维向量
# 参数：
#     Lambda: 折中参数
#     maxIter: 梯度下降法最大迭代步数
# 返回：
#    weight：回归方程的系数
class LASSO_ADMM:  
    def __init__(self, Lambda=1, maxIter=1000):
        self.lambda_ = Lambda
        self.maxIter = maxIter
    
    def soft_threshold(self, t, x):
        if x>t:
            return x-t
        elif x>=-t:
            return 0
        else:
            return x+t

    def fit(self, X, y):
        m,n = X.shape
        alpha = 2 * np.sum(X**2, axis=0) / m
        w = np.zeros(n)
        for t in range(self.maxIter):
            j = t % n
            w[j]=0
            e_j = X@(w.reshape(-1,1)) - y
            beta_j = 2 * X[:, j]@e_j / m
            u = self.soft_threshold(self.lambda_/alpha[j], -beta_j/alpha[j])
            w[j] = u
        self.w = w
    
    def predict(self, X):
        return X@(self.w.reshape(-1,1))

import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

def process_features(X):
    scaler = StandardScaler()
    X = scaler.fit_transform(X)
    m, n = X.shape
    X = np.c_[np.ones((m, 1)), X]  
    return X
    
housing = fetch_california_housing()
X = housing.data  
y = housing.target.reshape(-1,1)  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
X_train = process_features(X_train)
X_test = process_features(X_test)

model = LASSO_ADMM(Lambda=0.1, maxIter=1000)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
score = r2_score(y_test, y_pred)
print("mse = {}, r2 = {}".format(mse, score))