数据结构与算法一览（树、图、排序算法、搜索算法等）- Review

算法基础简介 - OI Wiki (oi-wiki.org)

文章目录

- - 1. 数据结构介绍
  - - 1.1 什么是数据结构
    - 1.2 数据结构分类
  - 2. 链表、栈、队列：略
  - 3. 哈希表：略
  - 4. 树
  - - 4.1 二叉树
    - 4.2 B 树与 B+ 树
    - 4.3 哈夫曼（霍夫曼）树：Huffman Tree
    - 4.4 线段树：略
    - 4.5 红黑树：简
  - 5. 图
  - - 5.1 图论概念
    - 5.2 图的存储
    - 5.3 最小生成树(Minimum Spanning Tree，MST)
    - - 5.3.1 定义
      - 5.3.2 最小生成树算法：Kruskal 算法-加边(边权从小到大)
      - 5.3.3 最小生成树算法：Prim 算法-加点(距离从小到大)
    - 5.4 最小直径生成树：略
    - 5.5 欧拉图：通过所有边且每条边恰好一次
    - 5.6 哈密顿图：所有顶点一次且且每个顶点恰好一次
    - 5.7 拓扑排序
    - 5.8 最短路
    - - 5.8.1 Floyd 算法
      - 5.8.2 Dijkstra 算法
  - X1. 排序算法
  - X2. 搜索（查找）算法
  - X3. Algorithm Coding

1. 数据结构介绍

1.1 什么是数据结构

数据结构是一门研究非数值计算的程序设计问题中的操作对象，以及它们之间的关系和操作等相关问题的学科。
数据结构是计算机中存储、组织数据的方式。

1.2 数据结构分类

线性表（线性表结构存储的数据往往是可以依次排列的，适合存储“一对一”关系的数据）
- 顺序表：顺序存储结构，底层实现借助的就是数组，简单理解为数组即可
- 链表：链式存储结构，使用链表存储数据时，是随用随申请，数据的存储位置是相互分离的
- 栈、队列：特殊的线性表，对线性表中元素的进出做了明确的要求
散列表：散列表源自于散列函数(Hash function)
树结构：适合存储具有“一对多”关系的数据
- 二叉树
- 堆
图结构：适合存储具有“多对多”关系的数据，在图结构中，数据结点一般称为顶点，而边是顶点的有序偶对

数据的运算是定义在数据的逻辑结构上的，但运算的具体实现要在存储结构上进行，一般有以下几种常用运算：

插入
删除
更新
排序
检索

2. 链表、栈、队列：略

栈：FILO
- 普通栈
- 单调栈
队列
- 普通队列
- 双端队列
- 优先权队列：堆

3. 哈希表：略

哈希函数
哈希碰撞
- 链式存储
- 二次哈希

4. 树

4.1 二叉树

二叉树
- 层序遍历
- 深度优先遍历
  - 前序遍历：先访问当前节点，再依次递归访问左右子树；
  - 中序遍历：先递归访问左子树，再访问自身，再递归访问右子树；
  - 后序遍历：先递归访问左右子树，再访问自身节点；
完整二叉树(full/proper binary tree)：每个结点的子结点数量均为 0 或者 2 的二叉树
完全二叉树(complete binary tree)：只有最下面两层结点的度数可以小于 2，且最下面一层的结点都集中在该层最左边的连续位置
完美二叉树(perfect binary tree)：所有叶结点的深度均相同的二叉树称为完美二叉树，也有叫满二叉树
二叉搜索树：也称为二叉查找树、二叉搜索树、有序二叉树或排序二叉树
- 定义
  1. 空树是二叉搜索树
  2. 若二叉搜索树的左子树不为空，左子树上所有节点的值都小于它的根节点
  3. 若二叉搜索树的右子树不为空，右子树上所有的节点的值都大于它的根节点
  4. 二叉搜索树的左右子树均为二叉搜索树
- 例子：
平衡二叉树：每一个结点的左子树和右子树高度差最多为 1
- 平衡状态不唯一：对于拥有同样元素值集合的平衡二叉树，平衡状态可能是不唯一的；也就是说，可能两棵不同的平衡二叉树，含有的元素值集合相同，并且都是平衡的
- 二叉树调整为平衡二叉树：右旋、左旋
AVL 树：平衡的二叉搜索树
- 性质：
  - 空二叉树是一个 AVL 树
  - 如果 T 是一棵 AVL 树，那么其左右子树也是 AVL 树，并且 $\leq 1$ ，h 是其左右子树的高度
  - 树高为 O(log n)
- 平衡因子：|右子树高度 - 左子树高度|
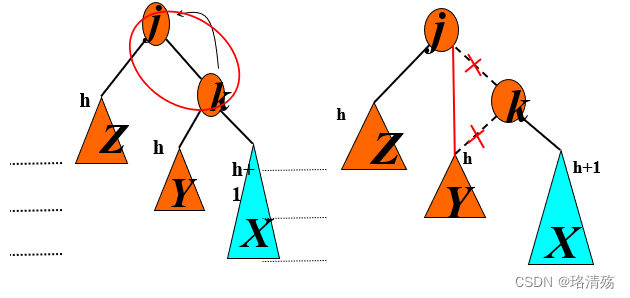
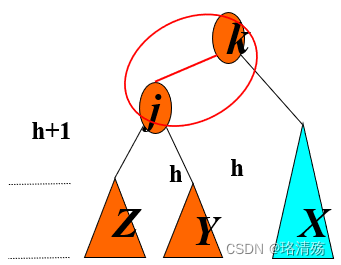
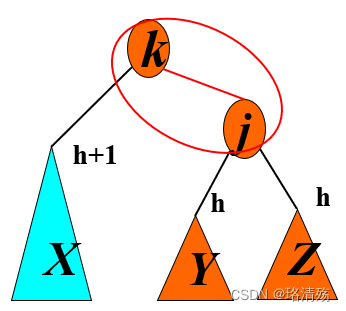
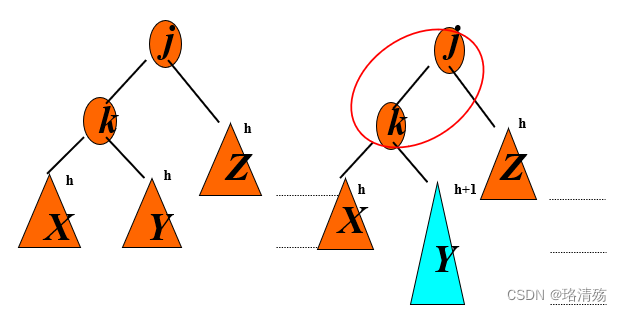
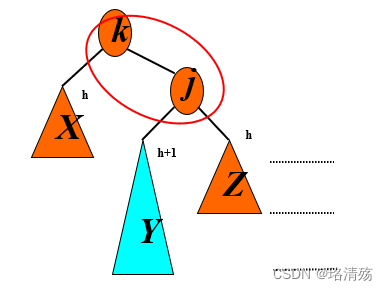
- 左旋
- 右旋
  - Case 1(Outside)
  - Case 2(Inside)

4.2 B 树与 B+ 树

B 树：B 树 (B-tree) 是一种自平衡的多叉树，能够保持数据有序
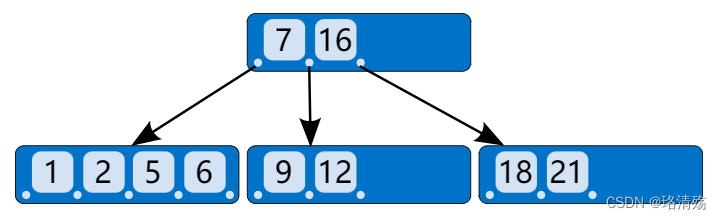
- 节点类型
  - 内部节点 (internal node)：存储了数据以及指向其子节点的指针
  - 叶子节点 (leaf node)：叶子节点只存储数据，不冗余存储内部节点
B+ 树：自平衡的多叉树

4.3 哈夫曼（霍夫曼）树：Huffman Tree

树的带权路径长度(Weighted Path Length of Tree，WPL)
- 从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 WPL
- 设 $w_i$ 为二叉树第 i 个叶结点的权值， $l_i$ 为从根结点到第 i 个叶结点的路径长度，则 WPL 计算公式如下：$WPL = $ $\sum_{i=1}^{n} w_il_i$
哈夫曼树
- 对于给定一组具有确定权值的叶结点，可以构造出不同的二叉树，其中 WPL 最小的二叉树称为 Huffman Tree
- 对于霍夫曼树来说，其叶结点权值越小，离根越远，叶结点权值越大，离根越近
哈夫曼算法：用于构造一棵霍夫曼树
哈夫曼编码
- 前缀编码：在设计不等长编码时，要考虑解码的唯一性，如果一组编码中任一编码都不是其他任何一个编码的前缀，那么称这组编码为 前缀编码，其保证了编码被解码时的唯一性
- 霍夫曼树可用于构造 最短的前缀编码，即 霍夫曼编码(Huffman Code)，其构造步骤为：

4.4 线段树：略

介绍
- 线段树是算法竞赛中常用的用来维护 区间信息 的数据结构
- 线段树可以在 $O (l o g n)$ 的时间复杂度内实现单点修改、区间修改、区间查询(区间求和，求区间最大值，求区间最小值)等操作
线段树的基本结构与建树
- 线段树将每个长度不为 1 的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，通过合并左右两区间信息来求得该区间的信息
  - 每个节点中用红色字体标明的区间，表示该节点管辖的数组 a = {10, 11, 12, 13, 14} 的位置区间
  - 通过观察不难发现， $d_i$ 的左儿子节点就是 $d_{2\times i}$ ， $d_i$ 的右儿子节点就是 $d_{2\times i+1}$ 。如果 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZgkZ80bo-1681661016143)(data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)] 表示的是区间 $[s, t]$ （即 $d_i=a_s+a_{s+1}+ \cdots +a_t$ )的话，那么 $d_i$ 的左儿子节点表示的是区间 $\frac{s+t}{2} ]$ ， $d_i$ 的右儿子表示的是区间 $[ \frac{s+t}{2} +1,t ] $。

4.5 红黑树：简

定义：红黑树是一种自平衡的二叉搜索树，每个节点额外存储了一个 color 字段 (“RED” or “BLACK”)，用于确保树在插入和删除时保持平衡
性质
- 节点为红色或黑色
- NIL 节点（空叶子节点）为黑色
- 红色节点的子节点为黑色
- 从根节点到 NIL 节点的每条路径上的黑色节点数量相同

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GRCtS8D0-1681661016143)(DS.assets/image-20230414195043342.png)]

5. 图

5.1 图论概念

图基本概念：
- 定义：图 (graph) 是一个二元组 $G = (V (G), E (G))$ ，其中 $V (G)$ 是非空集，称为 点集 (vertex set)，对于 V 中的每个元素，我们称其为 顶点 (vertex) 或 节点 (node)； $E (G)$ 为 $V (G)$ 各结点之间边的集合，称为 边集 (edge set)。
- 表示： $G = (V, E)$
  - 当 V, E 都是有限集合时，称 G 为有限图
  - 当 V 或 E 是无限集合时，称 G 为无限图
- 分类：
  - 无向图：边均为无向边
  - 有向图：边均为有向边， $\rightarrow v$ ，u 为 e 的起点，v 为 e 的终点，u 为 v 的直接前驱，v 为 u 的直接后继
  - 混合图：既有有向边也有无向边
  - 赋权图：图的每条边都被赋予一个数作为边的权
- 相邻：点边相邻、点点相邻
- 邻域：与某个点相邻的顶点构成的点集为该点的邻域
- 阶(order)：图的点数
- 度(degree)：与一个顶点关联的边的条数称作该顶点的度
  - 最大度、最小度
  - For 有向图：出度(以某个顶点为起点的边的数目称为该顶点的出度 out-degree) 与入度(以某个顶点为终点的边的数目称为该顶点的出度 in-degree)
- 途径(walk)：途径是连接一连串顶点的边的序列，可以为有限或无限长度，边的数量为途径的长度
  - 一条有限途径 w 是一个边的序列 $e_1, e_2, \ldots, e_k$ ，使得存在一个顶点序列 $v_0, v_1, \ldots, v_k$ 满足 $e_i = (v_{i-1}, v_i)$ ，其中 $\in [1, k]$ ，这样的途径可以简写为 $v_0 \to v_1 \to v_2 \to \cdots \to v_k$
- 迹(trail)：边两两不同的途径
- 路径(path)：点两两不同的途径
- 回路(circuit)：对于一条迹 w，若 $v_0 = v_k$ ，则称 w 是一条回路
稀疏图 & 稠密图
简单图：无自环和重边(multiple edge) 的图
k-正则图(k-regular graph)：若无向图的每个顶点的度数都是一个固定的常数 k，那么该图为 k-正则图
子图
- 子图：对一张图 $G = (V, E)$ ，若存在另一张图 $H = (V^{'}, E^{'})$ 满足 $V’ \subseteq V $且 $\subseteq E$ ，则称 H 是 !G 的子图 (subgraph)，记作 $\subseteq G$
- 生成子图/支撑子图：若 $\subseteq G$ 满足 $V^{'} = V$ ，则称 H 为 G 的生成子图/支撑子图 (spanning subgraph)
- 导出子图/诱导子图：若对 $\subseteq G$ ，满足 $\forall u, v \in V'$ ，只要 $\in E$ ，均有 $\in E'$ ，则称 H 是 G 的导出子图/诱导子图 (induced subgraph)
- 闭合子图：如果有向图 $G = (V, E)$ 的导出子图 $H = G \left[ V^\ast \right] $ 满足 $\forall v \in V^\ast, (v, u) \in E$ ，有 $\in V^\ast$ ，则称 H 为 G 的一个闭合子图 (closed subgraph)
连通图
- 无向图
  - 若无向图 $G = (V, E)$ ，满足其中任意两个顶点均连通（无向图中的连通也可以视作双向可达），则称 G 是连通图 (connected graph)，G 的这一性质称作连通性 (connectivity)
  - 连通分量(connected component)：即极大连通子图
- 有向图
  - 强连通：若一张有向图的节点两两互相可达，则称这张图是强连通的 (strongly connected)
    - 强连通分量：极大强连通子图
  - 弱连通：若一张有向图的边替换为无向边后可以得到一张连通图，则称原来这张有向图是弱连通的 (weakly connected)
    - 弱连通分量：极大弱连通子图
补图
- 对于无向简单图 $G = (V, E)$ ，它的补图 (complement graph) 指的是这样的一张图：记作 $\bar G$ ，满足 $\left( \bar G \right) = V \left( G \right)$ ，且对任意节点对 $(u, v)$ ， $\in E \left( \bar G \right)$ 当且仅当 $\notin E \left( G \right)$
反图
- 对于有向图 G = (V, E)，它的图 (transpose graph) 指的是点集不变，每条边反向得到的图
完全图 & 有向完全图
- 若无向简单图 G 满足任意不同两点间均有边，则称 G 为完全图 (complete graph)，n 阶完全图记作 $K_n$
- 若有向图 G 满足任意不同两点间都有两条方向不同的边，则称 G 为有向完全图 (complete digraph)
无边图：边集为空的图，记作 $\bar K_n$ (与 $K_n$ 互为补图)
二分图(Bipartite graph)：如果一张图的点集可以被分为两部分，每一部分的内部都没有连边，那么这张图是一张二分图 (bipartite graph)；如果二分图中任何两个不在同一部分的点之间都有连边，那么这张图是一张完全二分图 (complete bipartite graph)，一张两部分分别有 n 个点和 m 个点的完全二分图记作 $K_{m,n}$ .
平面图：如果一张图可以画在一个平面上，且没有两条边在非端点处相交，那么这张图是一张平面图 (planar graph).

5.2 图的存储

直接存边
- 方式
  - 使用一个数组来存边，数组中的每个元素都包含一条边的起点、终点以及边权(若有)
  - 使用多个数组分别存起点，终点和边权(若有)
- 应用场景：Kruskal 算法
邻接矩阵
- 使用一个二维数组 adj 来存边，其中 adj[u][v] 为 1 表示存在 u 到 v 的边，为 0 表示不存在(如果是带边权的图，可以在 adj[u][v] 中存储 u 到 v 的边的边权)
- 应用场景：稠密图
邻接表
- 使用一个支持动态增加元素的数据结构构成的数组来存边，如 list[u] 存储的是点 u 的所有出边的相关信息

Kruskal 算法：

Kruskal 算法是一种常见并且好写的最小生成树算法，由 Kruskal 发明，该算法的基本思想是从小到大加入边，是个贪心算法。

5.3 最小生成树(Minimum Spanning Tree，MST)

5.3.1 定义

生成树：一个连通无向图的生成子图且该子图为树(m 个节点，m - 1 条边)的子图就是生成树
- 只有连通图才有生成树，而对于非连通图，只存在生成森林
最小生成树：无向连通图的最小生成树(Minimum Spanning Tree，MST)为边权和最小的生成树

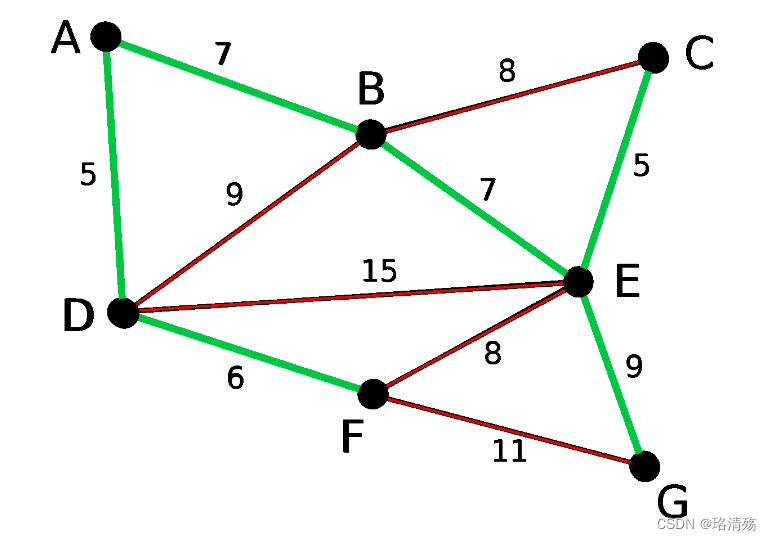
在这里插入图片描述

5.3.2 最小生成树算法：Kruskal 算法-加边(边权从小到大)

为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入，如果某次加边产生了环，就扔掉这条边，直到加入了 n-1 条边，即形成了一棵树。

5.3.3 最小生成树算法：Prim 算法-加点(距离从小到大)

每次要选择距离最小的一个结点，以及用新的边更新其他结点的距离。

5.4 最小直径生成树：略

在无向图的所有生成树中，直径最小的那一棵生成树就是最小直径生成树(树上任意两节点之间最长的简单路径即为树的「直径」)

5.5 欧拉图：通过所有边且每条边恰好一次

引入：哥尼斯堡七桥问题——遍历七桥一次返回起点？
- 非欧拉图，无解
定义
- 欧拉回路
  - 通过图中所有边且每条边恰好一次的回路
  - 通俗地说，对于一个图的某条路径，如果能从一个点出发将这个图的所有边都不重复地走一遍，那么这条路径就被称为欧拉路
- 欧拉(通)路
  - 通过图中所有边且每条边恰好一次的(通)路
  - 通俗地说，对于一个图的某条路径，如果能从一个点出发将这个图的所有边都不重复地走一遍并回到起点，那么这条路径就被称为欧拉回路
- 半欧拉图：具有欧拉通路但不具有欧拉回路的图
- 欧拉图：具有欧拉回路的图
性质
- 欧拉图中所有顶点的度数都是偶数
- 若 G 是欧拉图，则它为若干个环的并，且每条边被包含在奇数个环内
判别法
- 无向图：(a)是欧拉图，也是半欧拉图(具有欧拉通路)；©是半欧拉图；(b)两者都不是
  - 无向图为欧拉图：非零度顶点是连通的且顶点的度数都是偶数
  - 无向图为半欧拉图：非零度顶点是连通的、恰有 0 或 2 个奇度顶点
- 有向图：(b)是欧拉图，也是半欧拉图，© 是半欧拉图，(a)两者都不是
  - 有向图为欧拉图：非零度顶点是强连通的且每个顶点的入度和出度相等
  - 有向图为半欧拉图：非零度顶点是弱连通的、至多一个顶点的出度与入度之差为 1、至多一个顶点的入度与出度之差为 1 且其他顶点的入度和出度相等
算法
- Fleury 算法：略
- Hierholzer 算法：略

5.6 哈密顿图：所有顶点一次且且每个顶点恰好一次

引入：哈密顿提出的「周游世界」的游戏
- 把一个正十二面体(a)的二十个顶点看成地球上的二十个城市，要求游戏者沿棱线走，寻找一条经过所有结点一次且仅一次的回路(b)：
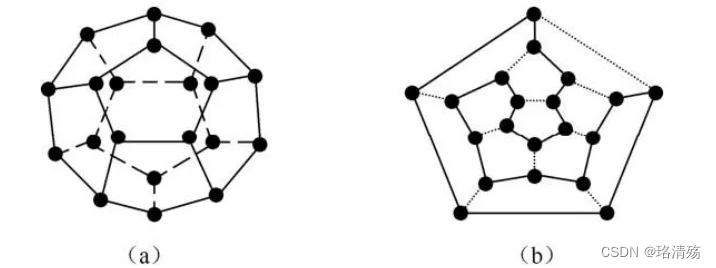
定义
- 哈密顿通路：通过图中所有顶点一次且仅一次的通路称为哈密顿通路
- 哈密顿回路(哈密顿圈)：通过图中所有顶点一次且仅一次的回路(除出发点外)称为哈密顿回路
- 半哈密顿图：具有哈密顿通路而不具有哈密顿回路的图称为半哈密顿图
- 哈密顿图：具有哈密顿回路的图称为哈密顿图，如(a)(b)；©有哈密顿通路；(d) 均无
性质：略
判别法：对于哈密尔顿图的判定，只能给出若干必要条件或充分条件，没有充要条件
- 充分条件：设 G 是 $\geq 3)$ 的无向简单图，若对于 G 中任意不相邻的顶点 $v_i, v_j$ ，均有 $d(v_i)+ d(v_j) \geq n$ ，则 G 中存在哈密顿回路，从而 G 为哈密顿图。
  - 通俗来讲，即对于顶点个数大于 2 的图，如果图中任意不相邻顶点的度和大于或等于顶点总数，那这个图一定是哈密顿图

5.7 拓扑排序

拓扑排序：在一个 DAG (有向无环图) 中，将图中的顶点以线性方式进行排序，使得对于任何的顶点 u 到 v 的有向边 $(u, v)$ ，都可以有 u 在 v 的前面
- 应用：用来判断图中是否有环、图是否是一条链
拓扑排序的目标是将 DAG 的所有节点排序(能拓扑排序的图一定为有向无环图)，使得排在前面的节点不能依赖于排在后面的节点
- 依赖：给定一个 DAG，如果从 i 到 j 有边，则认为 j 依赖于 i；如果 i 到 j 有路径(可达)，则称 j 间接依赖于 i.
拓扑排序算法
- Kahn 算法
  1. 初始：S-所有入度为 0 的点，L-空列表.
  2. 从 S 取出点 u 放入 L，把 u 的所有边删除，并改变边终点(v1, v2, …)的度(-1)，若终点入度为 0，放入 S.
  3. 重复直到 S 为空，检查图中是否存在任何边，如果有，那么这个图一定有环路，否则返回 L，L 中顶点的顺序就是拓扑排序的结果.
- DFS
  - 考虑一个图，删掉某个入度为 0 的节点之后，如果新图可以拓扑排序，那么原图一定也可以；反过来，如果原图可以拓扑排序，那么删掉后也可以

5.8 最短路

对于边权为正的图，任意两个结点之间的最短路，不会经过重复的结点
对于边权为正的图，任意两个结点之间的最短路，不会经过重复的边
对于边权为正的图，任意两个结点之间的最短路，任意一条的结点数不会超过 n，边数不会超过 n-1

5.8.1 Floyd 算法

适用于任何图，不管有向无向，边权正负，但是最短路必须存在

5.8.2 Dijkstra 算法

非负权图上单源最短路径

X1. 排序算法

稳定性是指相等的元素经过排序之后相对顺序是否发生了改变

冒泡排序(稳定)：工作原理是每次检查相邻两个元素，如果前面的元素与后面的元素满足给定的排序条件，就将相邻两个元素交换(当没有相邻的元素需要交换时，排序完成)
- 时间复杂度(平均)：O( $n^2$ )
- 时间复杂度(最优)：O(n)
- 时间复杂度(最差)：O( $n^2$ )
- 空间复杂度：O(1)

插入排序(稳定)：即将一个记录插入到已经排好序的有序表中，双层循环实现(外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动)

时间复杂度(平均)：O( $n^2$ )
时间复杂度(最优)：O(n)
时间复杂度(最差)：O( $n^2$ )

空间复杂度：O(1)

public class InsertionSort {
    public static void sort(Comparable[] arr){
        int n = arr.length;
        for (int i = 0; i < n; i++) {
           for (int j = i; j > 0; j--)
                if (arr[j].compareTo(arr[j-1]) < 0) {
                    swap(arr, j, j-1);
                } else {
                    break;
                }
        }
    }
    
    private static void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }
}

希尔排序(不稳定)：插入排序的一种，它是针对直接插入排序算法(如上)的改进，又称缩小增量排序，通过比较相距一定间隔的元素来进行，各趟比较所用的距离随着算法的进行而减小，直到只比较相邻元素的最后一趟排序为止
- 时间复杂度(平均)：O( $n^{3/2}$ ) \ O( $n log^2 n$ ) (取决于间距序列的选取)
- 时间复杂度(最优)：O(n)
- 时间复杂度(最差)：O( $n^{3/2}$ ) \ O( $n log^2 n$ ) (取决于间距序列的选取)
- 空间复杂度：O(1)
选择排序(不稳定)：其工作原理是每次找出第 i 小的元素（也就是 $A_{i...n}$ 中最小的元素)，然后将这个元素与数组第 i 个位置上的元素交换
- 时间复杂度(平均)：O( $n^2$ )
- 时间复杂度(最优)：O( $n^2$ )
- 时间复杂度(最差)：O( $n^2$ )
- 空间复杂度：O(1)
快速排序(不稳定)：又称分区交换排序，其通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列
- 时间复杂度(平均)：O(n logn)
- 时间复杂度(最优)：O(n logn)
- 时间复杂度(最差)：O( $n^2$ )
- 空间复杂度：O(logn)
  
  优化：二路快速排序、三路快速排序
归并排序(稳定)：建立在归并操作上的一种有效、稳定的排序算法，通过将已有序的子序列合并，得到完全有序的序列
- 时间复杂度(平均)：O(n logn)
- 时间复杂度(最优)：O(n logn)
- 时间复杂度(最差)：O(n logn)
- 空间复杂度：O(n)
堆排序(不稳定)：堆排序的本质是建立在堆上的选择排序（1. 从小到大排序：建立大顶堆，取出堆顶元素，与数组尾部的元素交换，并维持残余对的性质，依次类推 n - 1，即完成了从小到大的排序；2. 从大到小排序）
- 时间复杂度(平均)：O(n logn)
- 时间复杂度(最优)：O(n logn)
- 时间复杂度(最差)：O(n logn)
- 空间复杂度：由于可以在输入数组上建立堆，所以是一个原地算法
- 二叉堆
  - 定义：二叉堆通常是一个可以被看做一棵完全二叉树的数组对象
  - 性质：堆中某个节点的值总是不大于(小顶堆)或不小于(大顶堆)其父节点的值；二叉堆堆总是一棵完全二叉树(若完全二叉树的深度为 k，除第 k 层外，其它各层 (1～k-1) 的结点数都达到最大个数，第 k 层所有的结点都连续集中在最左边)
  - 存储：数组存储
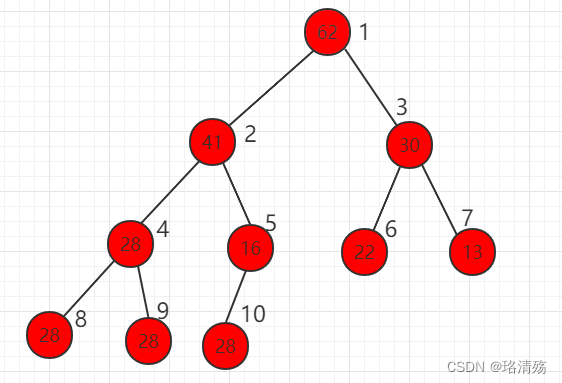
  - 堆的 shift up：往存储堆的数组末尾加入元素，根据堆的父子节点关系，判断是否满足堆(小堆或大堆)的性质，若不满足则交换元素(up)直到满足
  - 堆的 shift down：从堆中移除堆顶元素(根节点，即堆数组的第一个)，把数组最后一位放到根节点，根据堆的父子节点关系，判断是否满足堆(小堆或大堆)的性质，若不满足则交换元素(down)直到满足
  - 堆排序：从最后一个非叶子节点开始，分别把每个非叶子节点作为根节点进行 shift down 操作满足堆的性质直至根节点
基数排序(稳定)
桶排序
锦标赛排序(稳定)