题目
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
- 对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q,最近公共祖先LCA(T,p,q)表示一个节点x,满足x是p和q的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先。
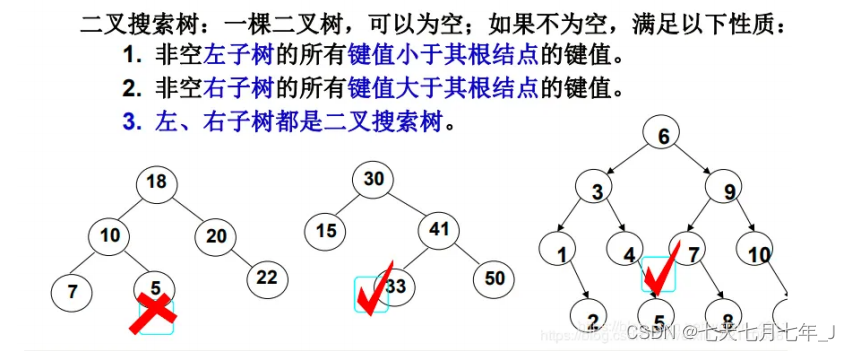
- 二叉搜索树是若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值。
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
数据范围:
3<=节点总数<=10000
0<=节点值<=10000
如果给定以下搜索二叉树: {7,1,12,0,4,11,14,#,#,3,5},如下图:
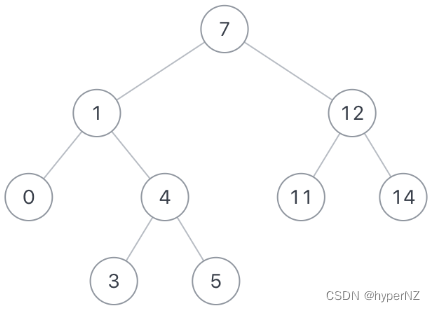
示例1
输入:{7,1,12,0,4,11,14,#,#,3,5},1,12
复制返回值:7
说明:节点1和节点12的最近公共祖先是7
示例2
输入:{7,1,12,0,4,11,14,#,#,3,5},12,11
返回值:12
说明:因为一个节点也可以是它自己的祖先.所以输出12
思路1:搜素路径比较
二叉搜索树是一种特殊的二叉树,它的每个节点值大于它的左子节点,且大于全部左子树的节点值,小于它右子节点,且小于全部右子树的节点值。因此二叉搜索树一定程度上算是一种排序结构。
二叉搜索树没有相同值的节点,因此分别从根节点往下利用二叉搜索树较大的数在右子树,较小的数在左子树,可以轻松找到p、q:
//节点值都不同,可以直接用值比较
while(node.val != target) {
path.add(node.val);
//小的在左子树
if(target < node.val)
node = node.left;
//大的在右子树
else
node = node.right;
}直接得到从根节点到两个目标节点的路径,这样利用路径比较就可以找到最近公共祖先。
具体做法:
- step 1:根据二叉搜索树的性质,从根节点开始查找目标节点,当前节点比目标小则进入右子树,当前节点比目标大则进入左子树,直到找到目标节点。这个过程成用数组记录遇到的元素。
- step 2:分别在搜索二叉树中找到p和q两个点,并记录各自的路径为数组。
- step 3:同时遍历两个数组,比较元素值,最后一个相等的元素就是最近的公共祖先。
代码
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
//求得根节点到目标节点的路径
public ArrayList<Integer> getPath(TreeNode root, int target) {
ArrayList<Integer> path = new ArrayList<Integer>();
TreeNode node = root;
//节点值都不同,可以直接用值比较
while (node.val != target) {
path.add(node.val);
//小的在左子树
if (target < node.val) {
node = node.left;
} else { //大的在右子树
node = node.right;
}
}
path.add(node.val);
return path;
}
public int lowestCommonAncestor(TreeNode root, int p, int q) {
//求根节点到两个节点的路径
ArrayList<Integer> path_p = getPath(root, p);
ArrayList<Integer> path_q = getPath(root, q);
int res = 0;
//比较两个路径,找到第一个不同的点
for (int i = 0; i < path_p.size() && i < path_q.size(); i++) {
int x = path_p.get(i);
int y = path_q.get(i);
//最后一个相同的节点就是最近公共祖先
if (x == y) {
res = path_p.get(i);
} else {
break;
}
}
return res;
}
}- 时间复杂度:O(n),设二叉树共有n个节点,因此最坏情况二叉搜索树变成链表,搜索到目标节点需要O(n),比较路径前半段的相同也需要O(n)。
- 空间复杂度:O(n),记录路径的数组最长为n。
思路2:一次遍历
递归是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。因此递归过程,最重要的就是查看能不能将原本的问题分解为更小的子问题,这是使用递归的关键。
而二叉树的递归,则是将某个节点的左子树、右子树看成一颗完整的树,那么对于子树的访问或者操作就是对于原树的访问或者操作的子问题,因此可以自我调用函数不断进入子树。
可以利用二叉搜索树的性质:对于某一个节点,
若是p与q都小于等于这个节点值,说明p、q都在这个节点的左子树,而最近的公共祖先也一定在这个节点的左子树;
若是p与q都大于等于这个节点值,说明p、q都在这个节点的右子树,而最近的公共祖先也一定在这个节点的右子树;
若是对于某个节点,p与q的值一个大于等于该节点值,一个小于等于该节点值,说明p、q分布在该节点的两边,而这个节点就是最近的公共祖先。
因此从上到下的其他祖先都将这个两个节点放到同一子树,只有最近公共祖先会将它们放入不同的子树,每次进入一个子树又回到刚刚的问题,因此可以使用递归。
具体做法:
- step 1:首先检查空节点,空树没有公共祖先。
- step 2:对于某个节点,比较与p、q的大小,若p、q在该节点两边说明这就是最近公共祖先。
- step 3:如果p、q都在该节点的左边,则递归进入左子树。
- step 4:如果p、q都在该节点的右边,则递归进入右子树。
代码
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @param p int整型
* @param q int整型
* @return int整型
*/
public int lowestCommonAncestor(TreeNode root, int p, int q) {
//空树找不到公共祖先
if (root == null) {
return -1;
}
//p、q在该节点两边说明这就是最近公共祖先
if ((p >= root.val && q <= root.val) || (p <= root.val && q >= root.val)) {
return root.val;
} else if (p <= root.val && q <= root.val) { //p、q都在该节点的左边
//进入左子树
return lowestCommonAncestor(root.left, p, q);
} else { //p、q都在该节点的右边
//进入右子树
return lowestCommonAncestor(root.right, p, q);
}
}
}- 时间复杂度:O(n),设二叉树共有n个节点,最坏情况递归遍历所有节点
- 空间复杂度:O(n),递归栈深度最坏为n