描述
若两个正整数的和为素数,则这两个正整数称之为“素数伴侣”,如2和5、6和13,它们能应用于通信加密。现在密码学会请你设计一个程序,从已有的 N ( N 为偶数)个正整数中挑选出若干对组成“素数伴侣”,挑选方案多种多样,例如有4个正整数:2,5,6,13,如果将5和6分为一组中只能得到一组“素数伴侣”,而将2和5、6和13编组将得到两组“素数伴侣”,能组成“素数伴侣”最多的方案称为“最佳方案”,当然密码学会希望你寻找出“最佳方案”。
输入:
有一个正偶数 n ,表示待挑选的自然数的个数。后面给出 n 个具体的数字。
输出:
输出一个整数 K ,表示你求得的“最佳方案”组成“素数伴侣”的对数。
数据范围: 1 ≤ n ≤ 100 1≤n≤100 1≤n≤100 ,输入的数据大小满足 2 ≤ v a l ≤ 30000 2≤val≤30000 2≤val≤30000 。
输入描述:
输入说明
1 输入一个正偶数 n
2 输入 n 个整数
输出描述:
求得的“最佳方案”组成“素数伴侣”的对数。
示例1
输入:
4
2 5 6 13
输出:
2
示例2
输入:
2
3 6
输出:
0
解法 匈牙利算法
题意整理如下:
- 如果两个正整数的和为素数,则这两个正整数称之为“素数伴侣”。
- 输入N(N为偶数)个正整数,从其中挑选出若干对组成“素数伴侣”。问怎么挑选,可以使得“素数伴侣”的对数最多。
不难发现,要使得大于等于2的两正整数之和为素数,则两个数必须要一奇一偶。我们首先定义两个数组,分别存储输入整数中的奇数和偶数。然后利用匈牙利算法找到“素数伴侣”对数最多时的配对数。匈牙利算法的核心思想是先到先得,能让就让。最后输出“素数伴侣”最多时的对数。
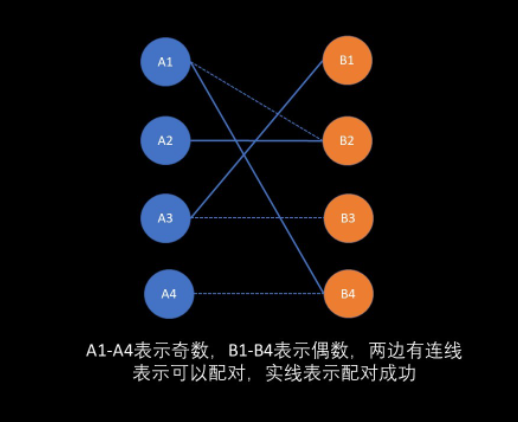
图解展示(匈牙利算法):
- 首先A1和B2配对(先到先得);
- 然后轮到A2,A2也可以和B2配对,这时B2发现A1还可以和B4配对,所以放弃了A1,选择和A2组成伴侣(能让就让)。
- 接着A3直接和B1配对(先到先得)。
- 最后A4尝试与B4配对,但这样A1就只能与B2配对,而A2就找不到伴侣了,一层层递归下来,发现不可行,所以A4不能与B4配对。
#include <iostream>
#include <vector>
#include <cstdlib>
#include <algorithm>
using namespace std;
const int maxn = 30010;
int n, a;
vector<int> odd, even;
bool vis[maxn];
int match[maxn];
bool np[maxn * 2] = {true, true, false};
void findPrimes() {
for (int i = 2; i < maxn * 2; ++i) {
if (!np[i]) { // 是素数
for (int j = i * i; j < maxn * 2; j += i) {
np[j] = true;
}
}
}
}
bool dfs(int x) {
for (int j = 0; j < even.size(); ++j) { // odd[i]都可能与even[j]构成素数
int y = even[j];
if (!vis[y] && !np[x + y]) {
vis[y] = true;
if (!match[y] || dfs(match[y])) {
match[y] = x; return true;
}
}
}
return false; // 找不到和odd[i]匹配的even[j]
}
int main() {
cin >> n;
findPrimes();
for (int i = 0; i < n; ++i) {
cin >> a;
if (a & 1) odd.push_back(a);
else even.push_back(a);
}
int ans = 0;
for (int i = 0; i < odd.size(); ++i) {
for (int j = 0; j < 30010; ++j) vis[j] = false;
if (dfs(odd[i])) ++ans;
}
printf("%d", ans);
}
// 64 位输出请用 printf("%lld")