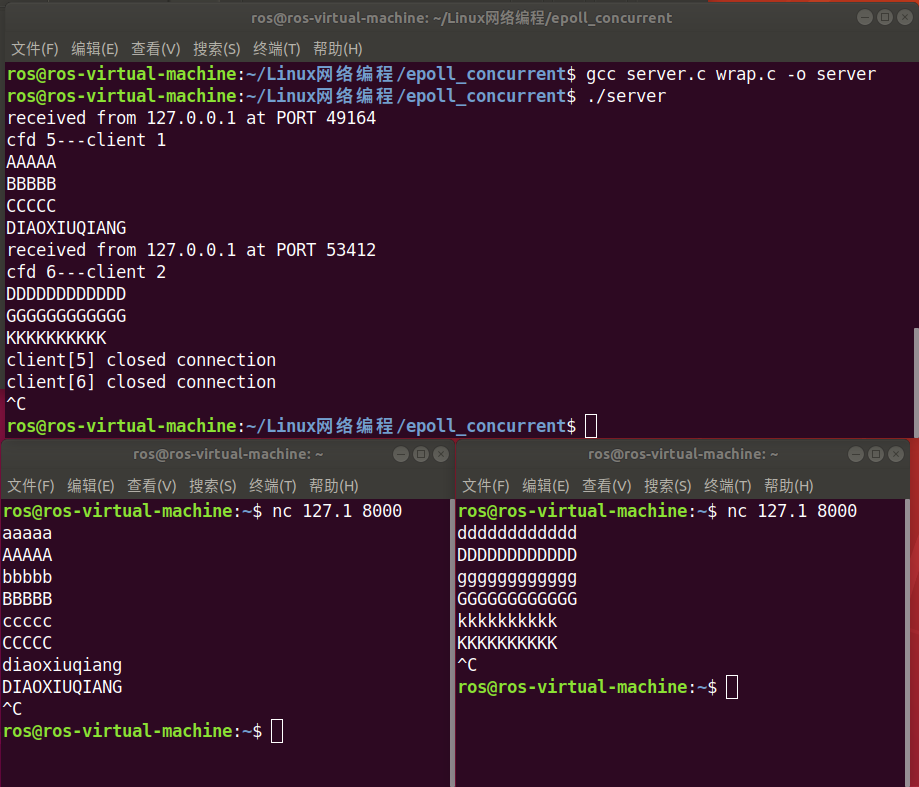
欢迎交流学习~~
专栏: 机器学习&深度学习
本文利用Python对数据集进行数据分析,并用多种机器学习算法进行分类预测。
具体文章和数据集可以见我所发布的资源:发布的资源
Python | 基于LendingClub数据的分类预测研究Part01——问题重述+特征选择+算法对比
- 零、问题重述&背景介绍
- 0.1 问题重述
- 0.2 背景介绍
- 一、不同特征对于预测结果差异的比较
- 1.1 LR算法的介绍
- 1.2 分类预测评价指标的介绍
- 1.3 Lending Club的数据描述与分析
- 1.4 特征选取与数据预处理
- 1.5 建模分析与结果比较
- 二、不同算法优劣的比较分析
- 2.1 算法的介绍
- 2.1.1 神经网络
- 2.1.2 贝叶斯分类器
- 2.2.2 决策树
- 2.2 建模分析与结果比较
- 2.2.1 神经网络
- 2.2.2 贝叶斯分类器
- 2.2.3 决策树
- 2.2.4 三种算法优劣势总结
零、问题重述&背景介绍
0.1 问题重述
-
问题一: 在数据集
lending-club中筛选不同属性,确定至少三组对应训练集及测试集,选用同一种机器学习算法,训练不同数据集,并进行实验结果比较分析。可进行数据均衡化预处理。 -
问题二: 选用不同的机器学习算法,对“多源数据”集完成分类预测(至少用三种机器学习算法实现,如支持向量机、神经网络、决策树等),并进行不同算法优劣的深入比较分析。可进行数据均衡化预处理。
-
问题三: 扩展内容,可针对某种机器学习算法,进行算法优化改进等操作,在完成本题目的问题一和问题二要求之后,创新性进行算法实验。
0.2 背景介绍
近年来随着网络时代的迅速发展,互联网金融产品迅猛发展起来,并逐步改变人类的生活和储蓄方式,大型的借贷平台也逐渐兴起,LendingClub 是其中一家发展迅速、运作较好的大型P2P(Peer to Peer)交易平台,由于P2P平台交易门槛低、流程简单、投资回报率高等优势,迅速吸引了大批量客户进入市场,从中也衍生出了一些违规贷款和欺诈事件,所以本文以Lending Club 公司的部分批贷数据进行建模分析,通过 Logistic Regression(LR) 分类预测的方法进行风险评估,提高 P2P 平台关于违约率较高客户的识别能力,从而为该平台及公司提供科学决策依据。
此外,本文针对“多源数据”集,选取 3 种机器学习算法:神经网络,贝叶斯分类器和决策树,深入比较多种算法之间的运算效果,分析各种算法的优势和劣势。
最后,本文针对 Lending Club 的批贷数据集和相关算法进行深入研究,将原来的二分类问题,变为三分类问题。进一步,在使用决策树这种单一树类模型进行分类后, 也使用两种集成树类算法——随机森林和极端随机树模型,对数据进行预测分类。最终,综合三种算法,比较了它们的优势和劣势。
一、不同特征对于预测结果差异的比较
该部分本文在对 Lending Club 数据集进行初步数据分析的基础上,通过选取 4 组不同的特征,采用同一种算法(逻辑回归,LR)进行分类预测,比较 4 组模型结果参数的差异,选出其中相对最优的特征。
1.1 LR算法的介绍
逻辑回归(Logistic Regression, LR)采用线性的方式进行分类,有效地将回归问题与分类问题进行了结合。
考虑二分类任务,其输出标记
y
∈
{
0
,
1
}
y\in \{0,1\}
y∈{0,1},而线性回归模型产生的预测值
z
=
w
T
x
+
b
z=w^{T}x+b
z=wTx+b 是实值,于是,我们需将实值
w
w
w 转换为
0
/
1
0/1
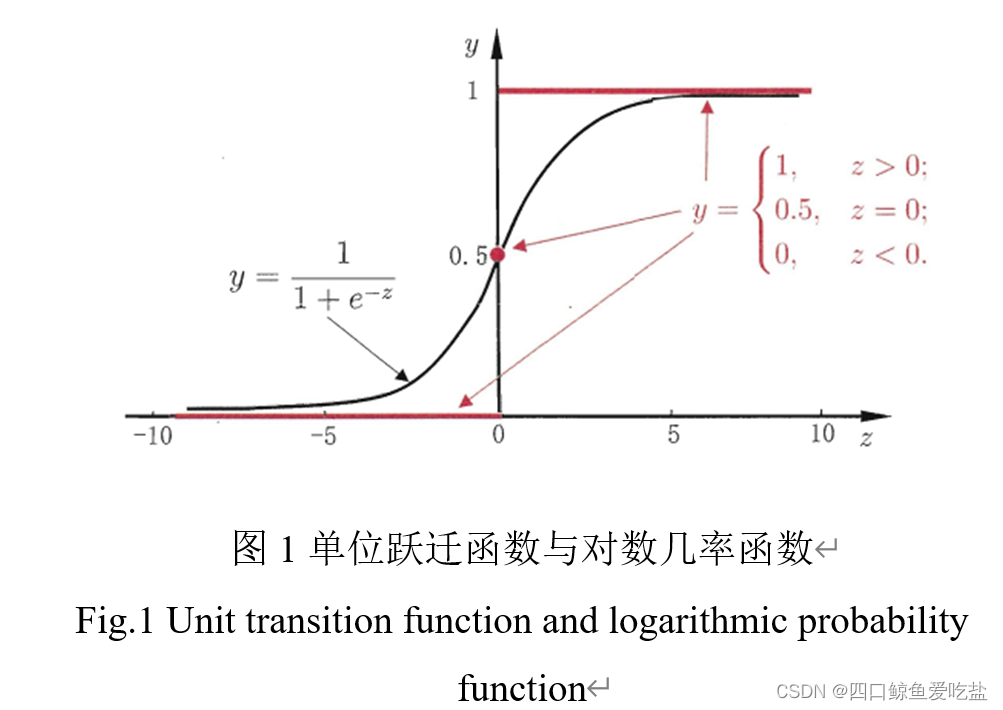
0/1 值。最理想的是“单位跃迁函数”:
y
=
{
0
,
z
<
0
0.5
,
z
=
0
1
,
z
>
0
y = \begin{cases}0, z<0 \\ 0.5, z=0 \\ 1, z>0 \end{cases}
y=⎩
⎨
⎧0,z<00.5,z=01,z>0
若预测值
z
z
z 大于零就判为正例,小于零则判为反例,预测值为临界值零则可以任意判别,但由于单位跃迁函数不连续,我们可以用对数几率函数:
y
=
1
1
+
e
−
z
y=\frac{1}{1+e^{-z}}
y=1+e−z1
来代替单位跃迁函数。单位跃迁函数和对数几率函数如图1:
将逻辑回归的公式进行整理,我们可以得到:
log
p
1
−
p
=
θ
T
x
\log \frac{p}{{1 - p}} = {\theta ^T}x
log1−pp=θTx
其中,
p
=
P
(
y
=
1
∣
x
)
p = P(y = 1|x)
p=P(y=1∣x) ,也就是将给定输入
x
x
x 预测为正样本的概率。在自变量
x
x
x 和超参数
θ
\theta
θ 确定的情况下,逻辑回归可以看作广义线性模型(Generalized Linear Models)在因变量
y
y
y 服从二元分布时的一个特殊情况。本文主要利用 Logistic Regression 在处理二分类问题时简单高效的优势,对本文的 Lending Club 数据进行分类预测。
1.2 分类预测评价指标的介绍
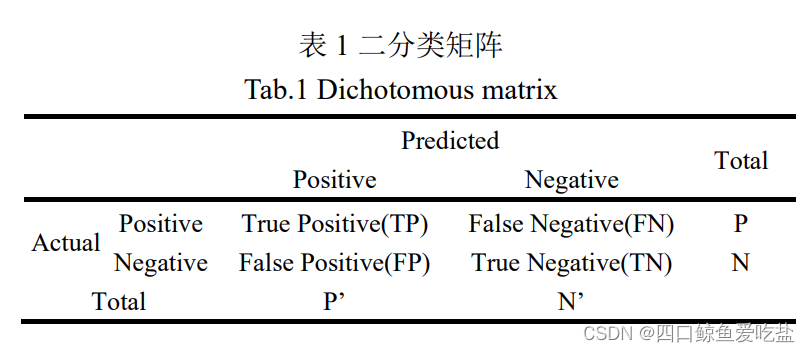
对于二分类问题,主要采用 Recall,Precision,Accuracy,F1-score,P-R曲线,ROC曲线,AUC曲线 等指标进行评价,在评价时可依据混淆矩阵来进行:
-
召回率(
Recall):分类正确的正样本个数占真正的正样本个数的比例: R e c a l l = T P T P + F N Recall = \frac{{TP}}{{TP + FN}} Recall=TP+FNTP -
准确率(
Precision):分类正确的正样本总数与分类器判别为正样本的样本总数的比例: P r e c i s i o n = T P T P + F P Precision = \frac{{TP}}{{TP + FP}} Precision=TP+FPTP -
F1-score:召回率和准确率的调和平均值,可以综合反应模型的性能: F 1 − s c o r e = 2 ⋅ R e c a l l ⋅ P r e c i s i o n R e c a l l + Pr e c i s i o n F1 - score = \frac{{2 \cdot Recall \cdot Precision}}{{{\mathop{\rm Re}\nolimits} call + \Pr ecision}} F1−score=Recall+Precision2⋅Recall⋅Precision -
P-R曲线:一个综合的图形指标,用来衡量分类模型的拟合效果,图形中横轴是Recall值,纵轴是Precision值。 -
正确率(
Accuracy):分类正确的样本个数占总样本个数的比例: A c c u r a c y = T P + T N T P + F P + T N + F N Accuracy = \frac{{TP + TN}}{{TP + FP + TN + FN}} Accuracy=TP+FP+TN+FNTP+TN -
ROC曲线:ROC曲线的横坐标为假阳性率(False Positive Rate, FPR),纵坐标为真阳性率(True Positive Rate, TPR)所构成的曲线。其中 F P R = F P N FPR = \frac{{FP}}{N} FPR=NFP, T P R = T P P TPR = \frac{{TP}}{P} TPR=PTP . -
AUC:是ROC曲线下的面积大小,该值能够量化反映出基于ROC曲线的模型性能,AUC值为沿着ROC曲线横轴的积分值,其值越接近于1,模型效果越好。
对于上述公式中字符的含义,可以用如下的二分类混淆矩阵表示:
1.3 Lending Club的数据描述与分析
本文数据是 Lending Club 公司对一段时间内贷款客户信息的整理,原始数据包含 77159 个样本,108 维特征,特征数据包含整型、浮点型、类别型和字符型的数据。预测变量为客户的贷款状态,包含的取值有:’Fully Paid’,’Current’,’Charged Off’,’Late (31-120 days)’,’In Grace Period’,’Late (16-30 days)’,’Default’,由于本文主要是为了识别违约客户,所以这里将 ’Fully Paid’ 和 ’Current’ 视为正常客户,标记为 0,其他情况的 ’Charged Off’,’Late (31-120 days)’,’In Grace Period’,’Late (16-30 days)’,’Default’ 视为违约客户,标记为 1.
接下来,本文针对客户的贷款状态以及某些特征进行初步数据分析:表2为正常客户和违约客户的统计信息,图2为不同贷款状态(loan_status)的客户数量统计图:
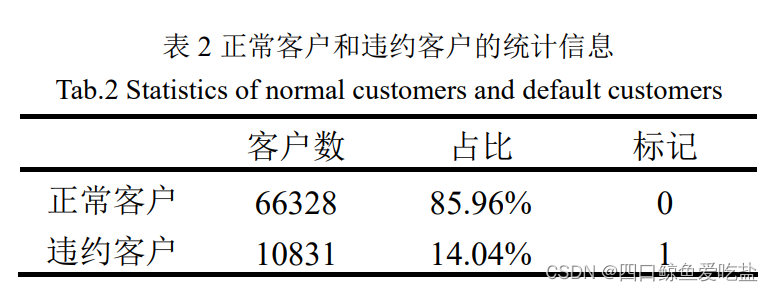
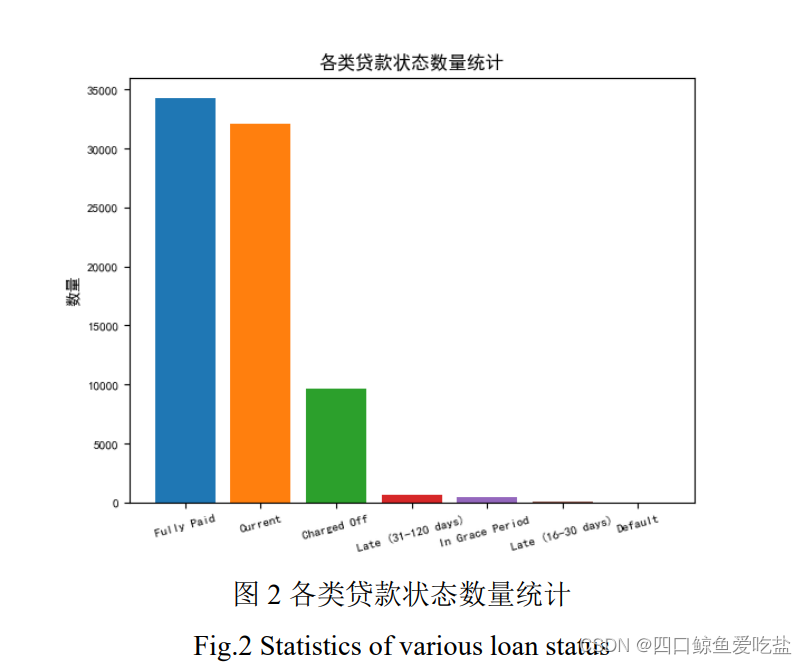
图3为贷款额度(loan_amnt)和贷款状态(loan_status)的箱型图,可以发现,随着贷款状况的下降,贷款额度呈现轻微上升趋势,可以猜测,二者有着一定的联系。
图4为不同信用等级(grade)的违约客户占比,可以看出随着信用等级由 A 向 F 降低,违约客户的占比越来越高,而 G 等级的违约客户占比较低,可能的原因是贷款公司对信用等级为 G 等级的用户审核条件更加严格。
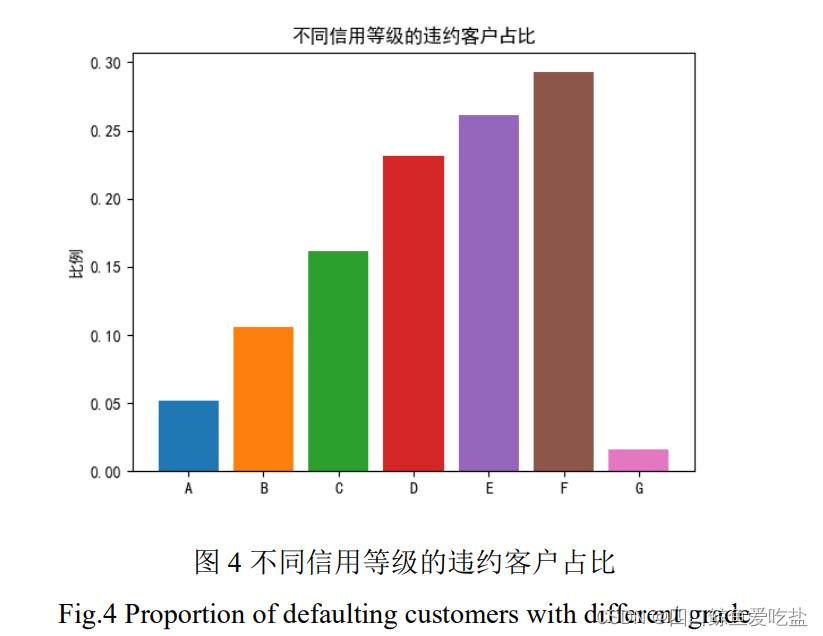
图5为不同总还款月份(term)的违约客户占比,可以看出:总还款月份为 60 个月的违约客户占比明显高于 36 个月的违约客户占比。推测可能的原因是前者的还款压力更大,工作不确定性也更大。
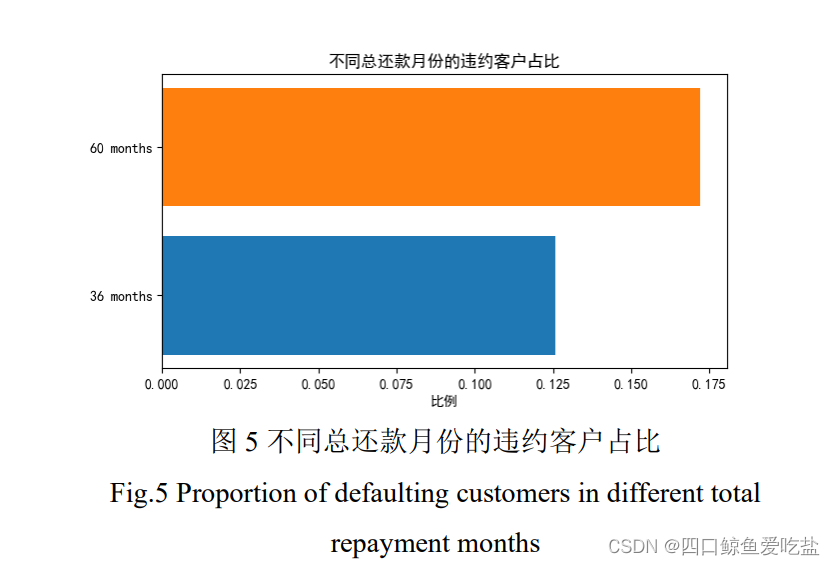
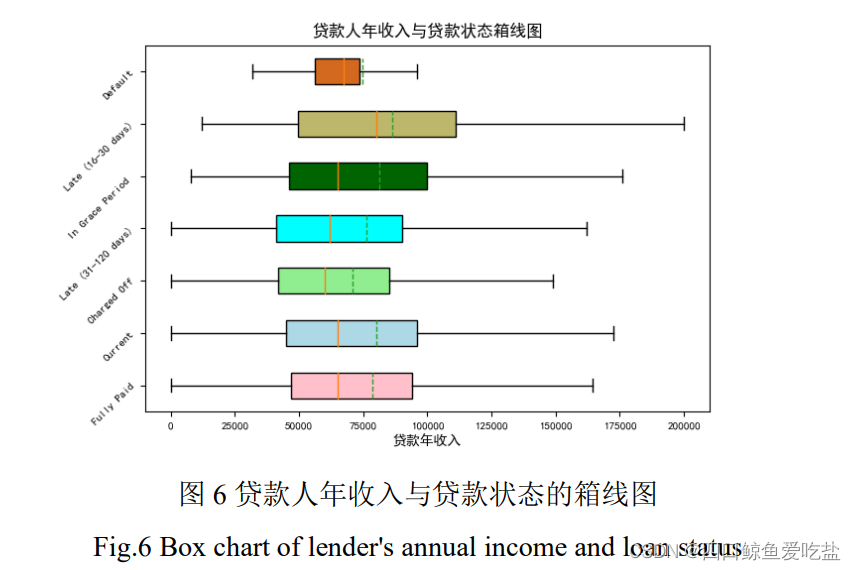
图6为贷款人年收入与贷款状态的箱线图,图中并未显示出两者之间存在着强相关关系。
1.4 特征选取与数据预处理
在上述数据的描述与分析的基础上,我们选取如下4组特征进行分析(表3):
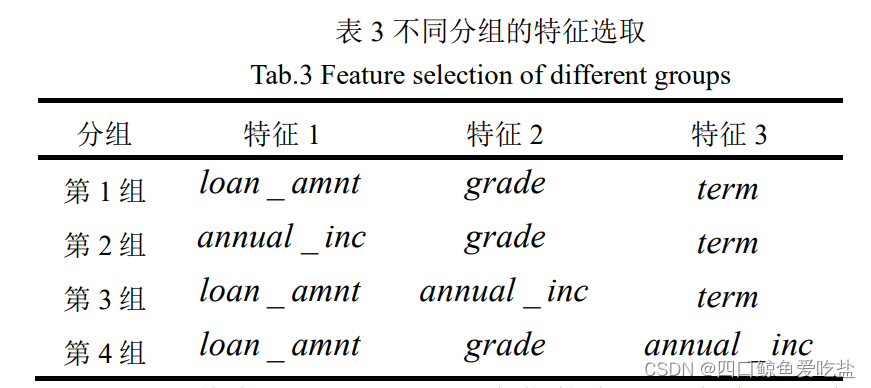
其中, loan_amnt为贷款金额,为连续型变量;grade 为信用等级,为类别变量;term 为总还款月份,为类别变量;annual_inc 为贷款人年收入,为连续型变量。
对于所选的特征,经过数据分析,不存在缺失值情况。而对于不同数据类型的特征,我们要采取不同的预处理方法:
- 类别变量
grade和term:
变量 中的A到G等级,分别标为0到6;变量 中的’36 months’标为0,’60 months’标为1. - 连续型变量
loan_amnt和annual_inc:
两者中的数据都进行标准化处理。
1.5 建模分析与结果比较
对于模型的建立与运算,我们要用到 python 中的numpy,pandas,sklearn 等包。对于数据集,我们都将其中的 80% 作为训练集,20% 作为测试集,绘制 4 个数据集模型对应的 ROC 曲线,如图7:
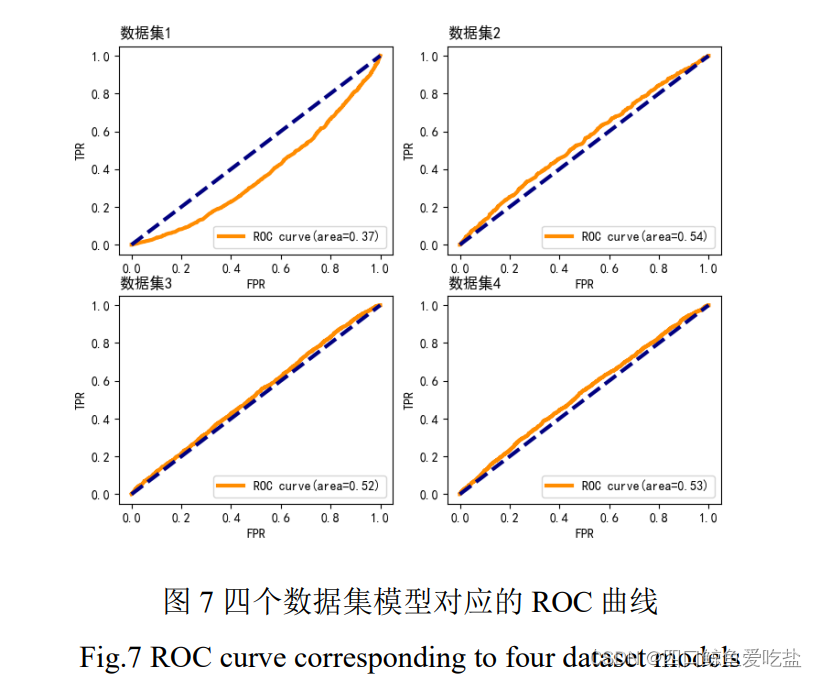
从图中我们可以看到,第2,3,4组的AUC值无明显差异,且显著高于第1组的值。
并得到各自的模型评价参数如下(表4):
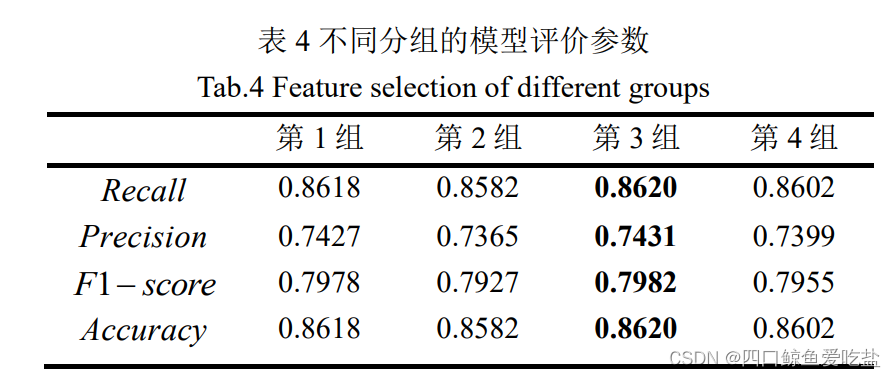
根据表中显示的不同分组的模型评价参数,我们可以发现:第3组的 Recall,Precision ,F1-score 和 Accuracy 都是最大的,因此我们我们可以认为第3组选择的特征:loan_amnt ,annual_inc ,term 对于违约客户的分类预测是相对最优的。
二、不同算法优劣的比较分析
该部分本文基于对“多源数据集”的分析,采用 3 种不同的机器学习算法:神经网络,贝叶斯分类器和决策树,对数据进行分类预测,并比较它们的模型评价参数,分析各个算法的优势和劣势。
2.1 算法的介绍
2.1.1 神经网络
人工神经元网络是对生物神经网络的一种模拟与近似,是由大量神经元通过相互连接而构成的自适应非线性动态网络系统。从提出的神经元第一个模型——MP模型,到单层感知器模型,再到提出一种按误差逆传播算法训练的多层前馈网络——反向传播网络(BP 网络)。
神经网络模型已经发展出多种形式,包括:卷积神经元(CNN),循环神经元(RC),长短期记忆神经元(LSTM),门控循环神经元(GRU),前馈神经网络(FFNN),径向基神经网络(RBF),霍普菲尔网络(HN)等。
如图8为一些神经网络图示:
2.1.2 贝叶斯分类器
贝叶斯分类器(Bayes法)是一种在已知先验概率与类条件概率的情况下的模式分类方法,待分类的分类结果取决于类域中样本的全体。
设训练样本集分为 M 类,记为
C
=
{
c
1
,
c
2
,
.
.
.
,
c
M
}
C = \{ {c_1},{c_2},...,{c_M}\}
C={c1,c2,...,cM},每类的先验概率为
P
(
c
i
)
P({c_i})
P(ci),当样本集非常大时,可以认为
P
(
c
i
)
=
n
(
c
i
)
n
P({c_i}) = \frac{{n({c_i})}}{n}
P(ci)=nn(ci),其中
n
(
c
i
)
n({c_i})
n(ci) 为
c
i
{c_i}
ci 类的样本数,
n
n
n 为总样本数。对于一个待分类样本
X
X
X,其归类为
c
i
c_{i}
ci类的类条件概率为
P
(
X
∣
c
i
)
P(X|{c_i})
P(X∣ci),根据Bayes定理,可得到后验概率为
P
(
c
i
∣
X
)
P({c_i}|X)
P(ci∣X):
P
(
c
i
∣
X
)
=
P
(
X
∣
c
i
)
P
(
c
i
)
P
(
X
)
P({c_i}|X) = P(X|{c_i})\frac{{P({c_i})}}{{P(X)}}
P(ci∣X)=P(X∣ci)P(X)P(ci)
若有 P ( c i ∣ X ) = max { P ( c j ∣ X ) } , j = 1 , 2 , . . . , M P({c_i}|X) = \max \{ P({c_j}|X)\} ,j = 1,2,...,M P(ci∣X)=max{P(cj∣X)},j=1,2,...,M,则有 X ∈ c i X \in {c_i} X∈ci,这就是最大后验概率判别准则,也是常用的Bayes分类判决准则。经过长期的研究,Bayes分类方法在理论上论证得比较充分,在应用上也是非常广泛的。
2.2.2 决策树
决策树可看作一个树状预测模型,它通过把实例从根节点排列到某个叶子节点来分类实例,叶子结点即为实例所属的分类。决策树的核心问题是选择分裂属性和决策树的剪枝。
决策树的算法有很多,有 ID3,C45,CART 等等。这些算法均采用自顶向下的贪婪算法,每个节点选择分类效果最好的属性将节点分裂为 2 个或多个子结点,继续这一过程知道这棵树能准确地分类训练集,或所有属性都已经被使用过。
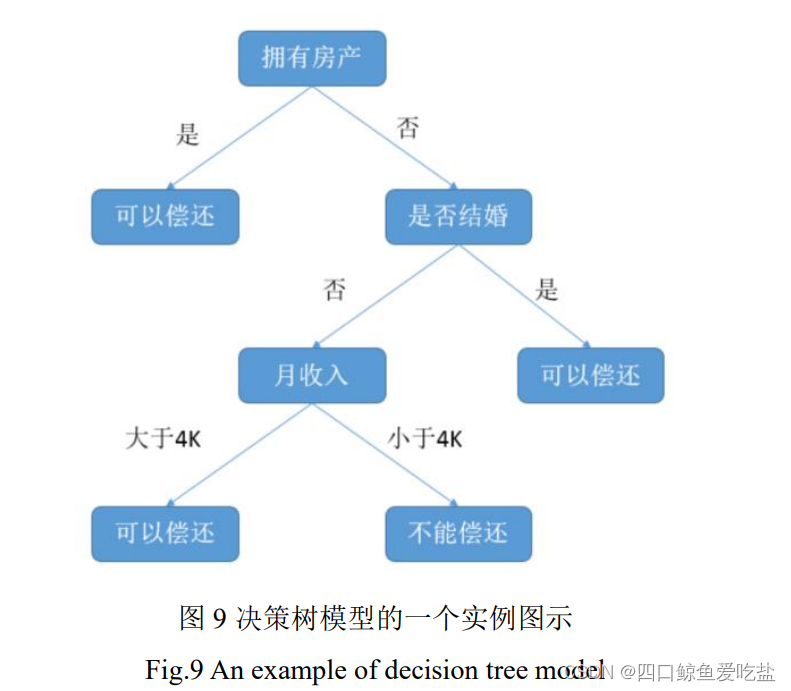
图9是用决策树判断是否能偿还贷款的实例原理图示:
2.2 建模分析与结果比较
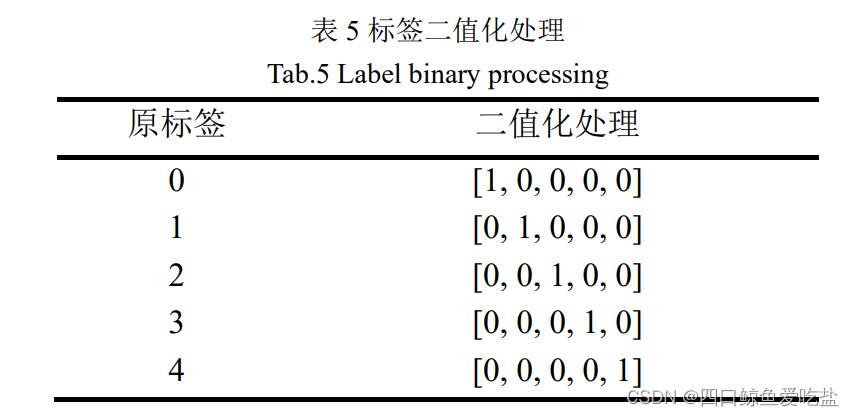
由于“多源数据集”中已经给出处理之后的“编码多源数据集”,因此该部分我们直接对编码多源数据集进行预处理。而对于多分类情况,我们除了1.3中提到的预处理方法,我们也可以将标签进行二值化处理(表5):
对于模型的建立与运算,我们要用到 python 中的 numpy,pandas,sklearn等包。对于数据集,我们都将其中的 80% 作为训练集,20% 作为测试集。之后,我们采用三种机器学习算法建立模型,并统计各种算法的性能:
2.2.1 神经网络
本文根据经验公式:
λ
=
m
+
n
+
α
\lambda = \sqrt {m + n} + \alpha
λ=m+n+α
设置隐含层节点数目,其中
λ
\lambda
λ 为隐含层节点数,
m
m
m 为输入层节点数目,对于该数据集为 26,
n
n
n 为输出层结点数,为 5, 为 1~10的常数,这里设为 4,最终计算结果四舍五入,得到
λ
=
10
\lambda=10
λ=10.
表6为采用神经网络的模型结果参数:
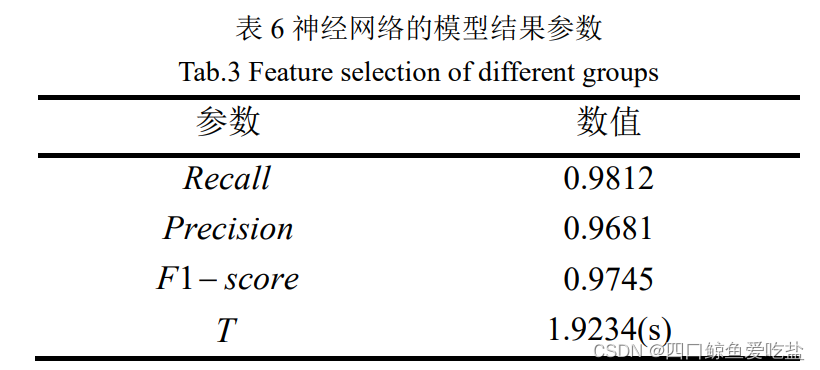
其中, 表示算法运行总时长,单位为秒(s).
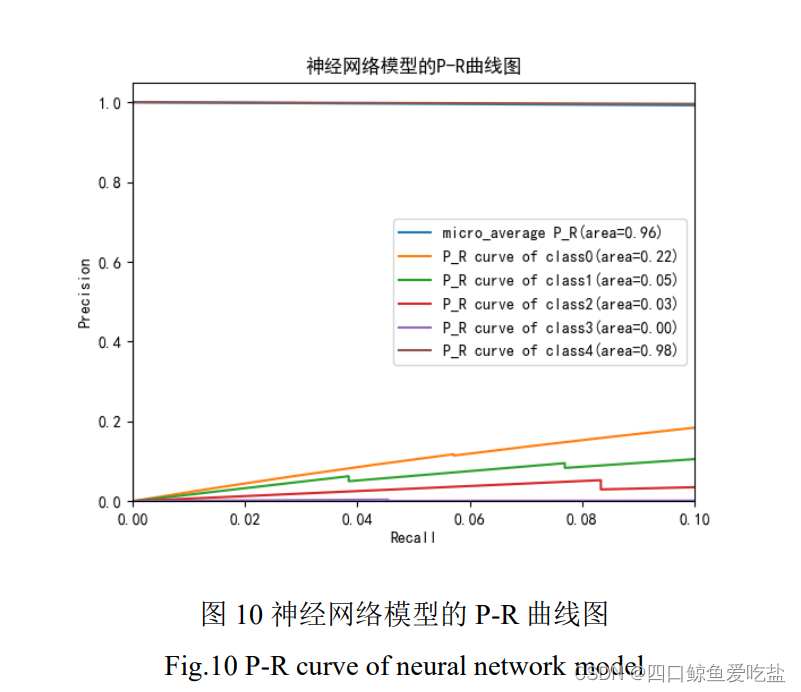
图10是神经网络模型的 P-R 曲线图,其中类别 0,1,2 的准确率随着召回率的提高而上升,类别3的准确率却维持在 0,类别 4 的准确率一直维持在较高水平,总体的平均准确率也一直维持在较高水平。
2.2.2 贝叶斯分类器
表7为采用贝叶斯分类器的模型结果参数:
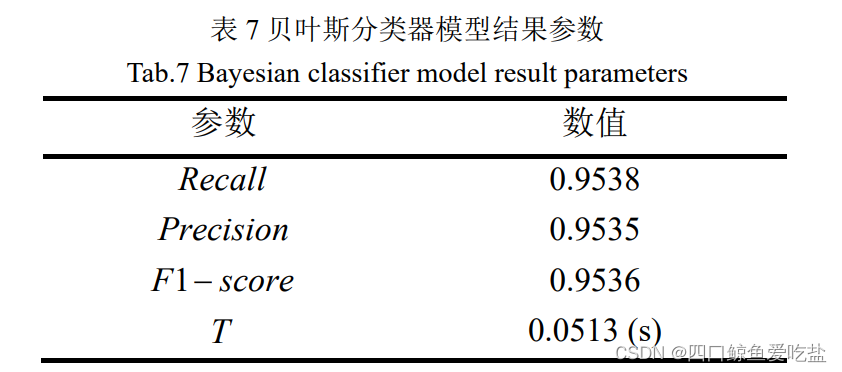
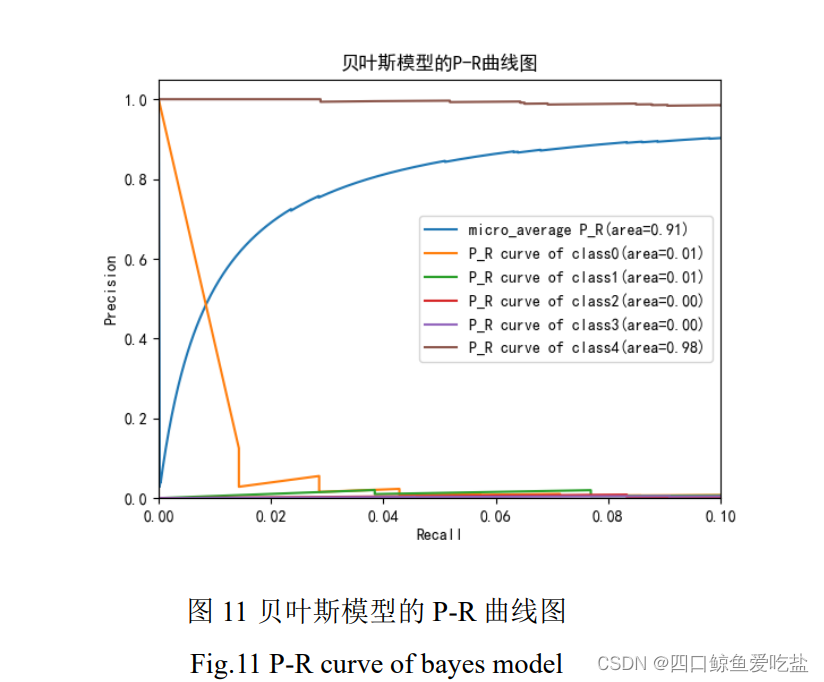
图11是贝叶斯分类器模型的 P-R 曲线图,类别 0 的准确率随着召回率的上升而快速下降,类别 1,2,3 的准确率一直维持在较低水平,类别 4 的准确率一直处于较高水平,而总体平均准确率随着召回率提高而不断提高。
2.2.3 决策树
表8为采用决策树的模型结果参数:
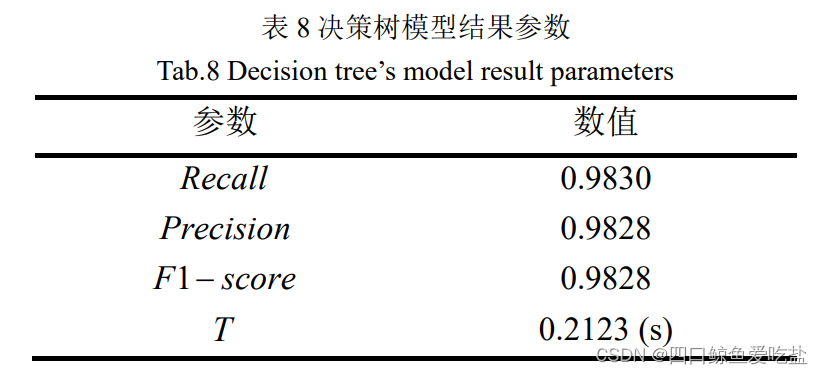
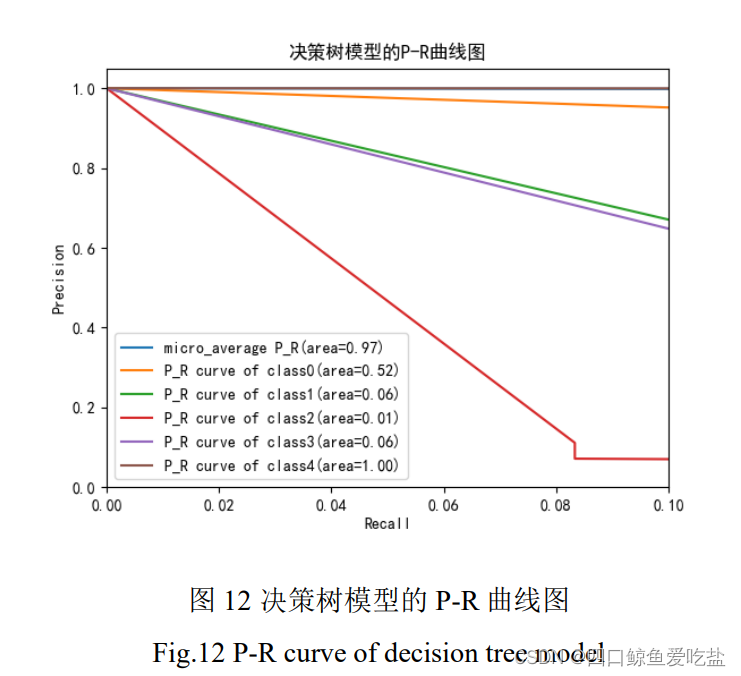
图12是决策树模型的P-R曲线图,模型中各类的准确率都随着召回率的提高而下降,下降速度不同,但是总体平均准确率也一直维持在较高水平。
2.2.4 三种算法优劣势总结
神经网络模型的召回率(Recall),准确率(Precision)和 F1-score 都高于贝叶斯分类器,但是模型运行时间过长。
贝叶斯分类器的召回率(Recall),准确率(Precision)和 F1-score 都较低,但是其模型运行时间是三者最短的。
决策树的召回率(Recall),准确率(Precision)和F1-score 都是三者最高的,而且相比于神经网络,其运行时间也显著偏低。
综合三种算法,决策树模型的准确度和泛化能力最优,且相比于贝叶斯分类的运行时间,决策树的运行时间也属于可接受范围内,因此我们可以认为,三者之间决策树模型最优。