前向概率

给定隐马尔可夫模型$\lambda$，定义到时刻$t$部分观测序列为$o_1,o_2,\cdots ,o_t$且状态为$s_i$的概率为前向概率，记作${\alpha }_t(i)=P(o_1,o_2,\cdots ,o_t,i_t=s_i|\lambda )$。可以递推地求出前向概率${\alpha }_t(i)$以及观测序列概率$P(O|\lambda )$

模型基础参数

公式推导

（1）初值
$${\alpha }_1(i)={\pi }_i{b}_i(o_1),i=1,2,\cdots ,N$$

第一个时刻，i代表不同的状态，pi表示初始概率，b为发射概率，如：从5个盒子中抽球，第一个抽到红球，i对应的就是1，b为红球在第一个盒子中被抽出来的概率（发射概率）
结果是5个数据，第i数据表示第1个时刻从第i球中抽出红球的概率

（2）递推 对$t=1,2,\cdots ,T-1$
$$\begin{gathered} {\alpha }_{t+1}(i)=\left[\sum _{j=1}^N{\alpha }_t(j)a_{ji}\right]b_i(o_{t+1}),i=1,2,\cdots ,N \\ 示例t=1,i=1 \\ {\alpha }_2(1)=\left[\sum _{j=1}^N{\alpha }_1(j)a_{j1}\right]b_1(o_2) \\ t=1,i=2 \\ {\alpha }_2(2)=\left[\sum _{j=1}^N{\alpha }_1(j)a_{j2}\right]b_2(o_2) \\ t=1,i=3 \\ {\alpha }_2(3)=\left[\sum _{j=1}^N{\alpha }_1(j)a_{j3}\right]b_3(o_2) \end{gathered}$$

第二个时刻则是前一个时刻求出的5个数据，每个数据乘转移概率和再乘当前时刻的发射概率
a(t)j表示上个时刻求出的5个值，aji表示从j状态转移到i状态的概率

（3）终止
$$P(O|\lambda )=\sum _{i=1}^N{\alpha }_T(i)$$

概率求和（算出的5个状态分别对应的值进行求和）

代码实现

随机从4个盒子中抽出5个球 ，求该序列的概率
前向概率计算函数：forward_probability()其中是通过矩阵运算，所以公式的求和的符号可能提现的不明显，可以输出运算后结果进而理解运算过程

import numpy as np

class HMM(object):
    def __init__(self, N, M, pi=None, A=None, B=None):
        self.N = N # 盒子数量
        self.M = M # 球颜色数量
        self.pi = pi # 初始概率向量
        self.A = A # 转移概率矩阵
        self.B = B # 观测概率矩阵

    def get_data_with_distribute(self, dist):
        # 根据给定的概率分布，返回一个索引
        return np.random.choice(np.arange(len(dist)), p=dist)

    def generate(self, T : int):
        # T 要生成的数据的数量
        # 根据给定额参数生成观测序列
        # 根据初始概率分布，获取从哪个盒子取第一个球
        z = self.get_data_with_distribute(self.pi) # 得到的是第一个盒子的编号
        # 从上一个盒子中根据观测概率选中一个球（颜色）
        x = self.get_data_with_distribute(self.B[z]) #x代表球的颜色，0红色 1白色
        result = [x]
        for _ in range(T-1):
            z = self.get_data_with_distribute(self.A[z]) # 得到下一个盒子
            x = self.get_data_with_distribute(self.B[z]) # 从该盒子中随机选中一个颜色
            result.append(x)

        return result

    def forward_probability(self, X):
        # 根据给定的观测序列X，计算观测序列出现的概率
        alpha = self.pi * self.B[:, X[0]]
        # print(type(alpha))

        for x in X[1:]:
            # print(alpha)
            # print(self.A)
            # print(np.matmul(alpha, self.A))
            alpha = np.matmul(alpha, self.A) * self.B[:, x]

        return alpha.sum()


if __name__ == '__main__':
    pi = np.array([.25, .25, .25, .25])
    A = np.array([
        [0,  1,  0, 0],
        [.4, 0, .6, 0],
        [0, .4, 0, .6],
        [0, 0, .5, .5]])
    B = np.array([
        [.5, .5],
        [.3, .7],
        [.6, .4],
        [.8, .2]])
    assert len(A) == len(pi)
    assert len(A) == len(B)
    hmm = HMM(B.shape[0], B.shape[1], pi, A, B)
    seq = hmm.generate(5)
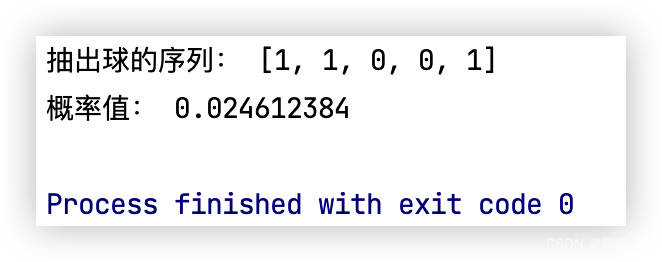
    print('抽出球的序列：', seq)

    print('概率值：', hmm.forward_probability(seq))

结果：白白红红白

心得：通过理解公式后再去理解运算过程和代码会很简单，关于矩阵运算对应到公式起初理解困难，多思考，多打印结果值，理解每步后方可打通任督二脉