前言
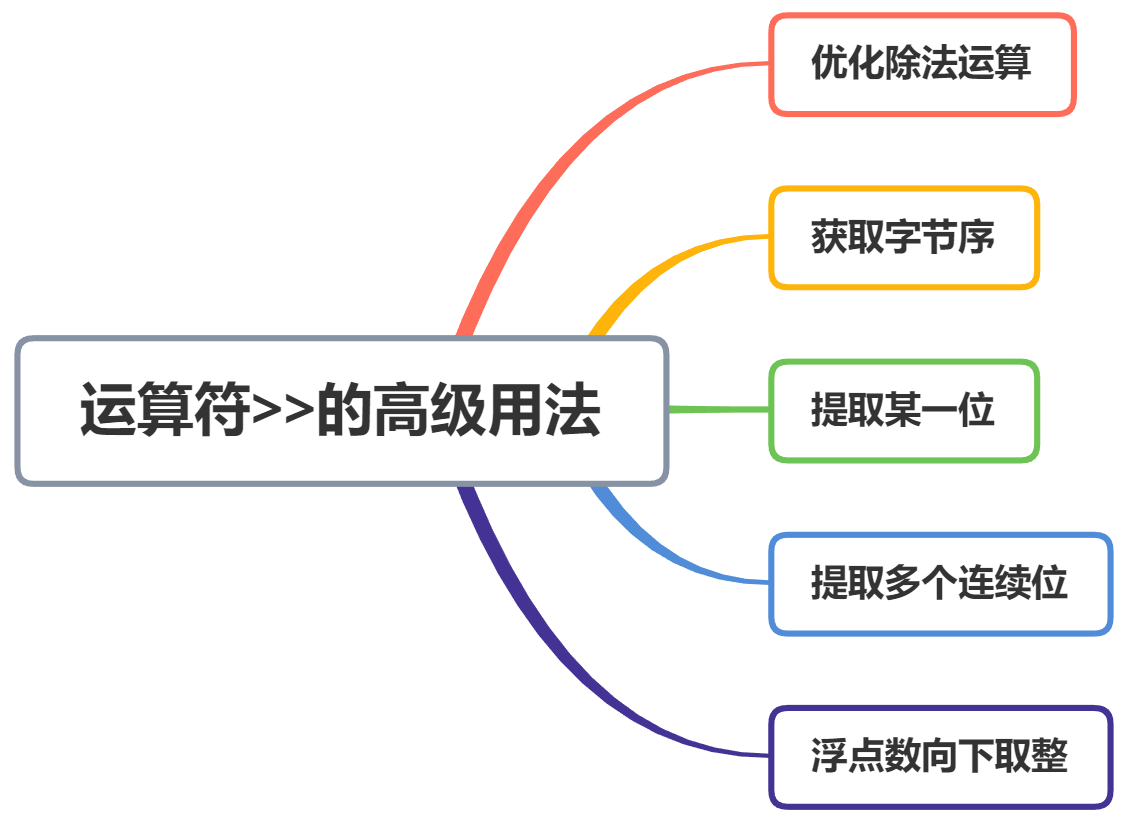
在上一篇文章中,我们介绍了<<运算符的高级用法,本篇文章,我们将介绍>> 运算符的一些高级用法。
一、人物简介
- 第一位闪亮登场,有请今后会一直教我们C语言的老师 —— 自在。

- 第二位上场的是和我们一起学习的小白程序猿 —— 逍遥。

二、优化除法运算
-
除法运算需要比位移运算需要更多的计算资源,某些情况下采用位移运算可以提高性能
-
代码示例
#include <stdio.h>
int main()
{
int a = 1024;
int b = a / 8; // 整除8
int c = a >> 3; // 相当于除以8
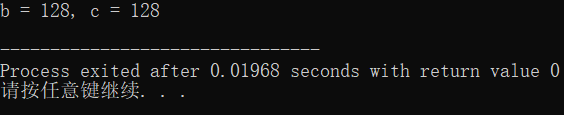
printf("b = %d, c = %d\n", b, c);
return 0;
}
- 每右移一位相当于除以2,
a >> 3相当于a/(2*2*2) = a/8; - 运行结果
三、获取字节序
-
大端模式:是指数据的高字节保存在内存的低地址中,而数据的低字节保存在内存的高地址中。
-
小端模式:是指数据的高字节保存在内存的高地址中,而数据的低字节保存在内存的低地址中。
-
右移运算符还可以用于获取当前系统的字节序(即大端序或小端序)
-
比如数字 0x1234在内存中的表示形式为:
大端模式:
低地址 -----------------> 高地址
0x12 | 0x34小端模式:
低地址 ------------------> 高地址
0x34 | 0x12 -
代码示例
#include <stdio.h>
int main()
{
short int i = 0x1234; // 假设i在内存中的地址为0x1000
char *p = (char *)&i; // 将i的地址转换为字符型指针,即指向0x1000的字节型指针
if (*p == 0x12) // 判断*p的值是否等于0x12,如果等于则为大端序,否则为小端序
{
printf("大端序\n");
}
else
{
printf("小端序\n");
}
return 0;
}
- 运行结果

四、提取二进制数的某一位
- 将一个二进制数右移n位,再与1进行按位与运算,得到的结果就是这个二进制数的第n位(从第0位开始算)
- 例如,将1011右移2位,得到的结果是10,再与1进行按位与运算,得到的结果是0,即1011的第二位是0
- 代码示例
#include <stdio.h>
int main()
{
int a = 0b1011;
int b = (a >> 2) & 1; // 提取a的第二位,即0
printf("第二位的值为 %d\n", b);
return 0;
}
- 运行结果

五、提取二进制数的多个连续位
- 将一个二进制数右移n位,再与一个掩码进行按位与运算,得到的结果就是这个二进制数从第n位开始的若干位
- 例如,将
1011011右移3位,得到的结果是1011,再与111进行按位与运算,得到的结果是011,即1011011从第3位开始的三位是011 - 代码示例
#include <stdio.h>
int main()
{
int a = 0b1011011;
int b = (a >> 3) & 0b111; // 提取a从第3位开始的3位,即101
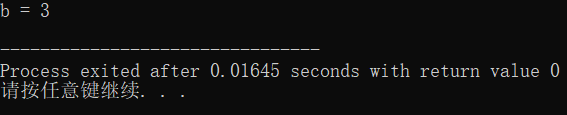
printf("b = %d\n", b);
return 0;
}
- 运行结果,3 (二进制为0b
011)
六、浮点数向下舍入为整数
-
这种用法通常用于嵌入式系统中,因为某些嵌入式处理器没有浮点数运算单元,只能使用整数运算单元来处理浮点数
-
将一个浮点数乘以一个定点数的精度,并将结果向下取整,可以得到一个整数近似值
-
例如,将一个浮点数乘以1000,再将结果右移10位,得到的结果就是这个浮点数乘以1000并向下取整的整数值
-
代码示例
#include <stdio.h>
int main()
{
float x = 3.1415926;
int a = (int)(x * 1000.0f) >> 10; // 将x乘以1000并向下取整
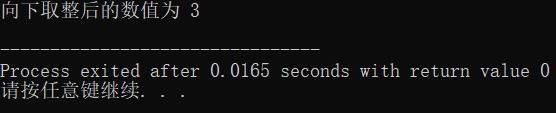
printf("向下取整后的数值为 %d\n", a);
return 0;
}
- 运行结果
小结
通过这篇文章,我们学会了用位运算符>>的5种高级用法
1、优化除法运算
2、获取字节序
3、提取二进制数的某一位
4、提取二进制数的多个连续位
5、浮点数向下舍入为整数
📢欢迎各位 👍点赞 ⭐收藏 📝评论,如有错误请留言指正,非常感谢!