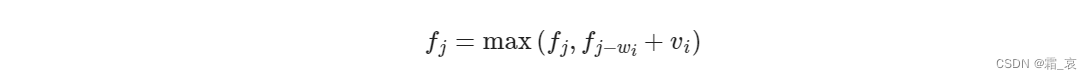【DES详解】（一）处理input block(64 bits)

一、DES 加密算法总览

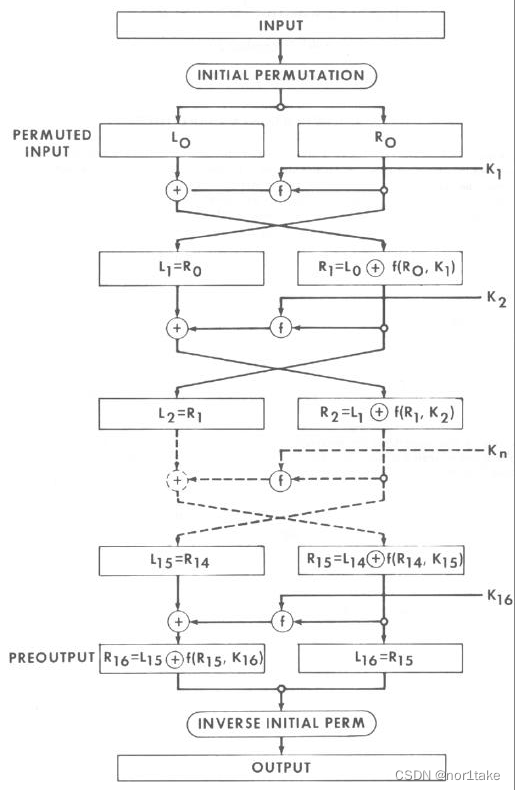
DES 算法总览

0-1、初识置换 IP（Initial Permutation）

输入：明文（64 bits）
过程：初识置换
输出：处理后的明文permuted input（64 bits）

首先，对需要解密的input block(64 bits)进行如下置换，称之为 初识置换（Initial Permutation, IP）。

置换（Permutation） 是古典密码中另一种基本的处理技巧，就是将明文中的字母重新排列，字母本身不变，只是改变其位置。

//Operation.java
public int[][] ip = new int[][]{
        {58, 50, 42, 34, 26, 18, 10, 2},
        {60, 52, 44, 36, 28, 20, 12, 4},
        {62, 54, 46, 38, 30, 22, 14, 6},
        {64, 56, 48, 40, 32, 24, 16, 8},
        {57, 49, 41, 33, 25, 17, 9, 1},
        {59, 51, 43, 35, 27, 19, 11, 3},
        {61, 53, 45, 37, 29, 21, 13, 5},
        {63, 55, 47, 39, 31, 23, 15, 7}
};

如何根据表，进行置换操作？

第1行第1列的数 = 58 表示将明文中的第58位的数放到第1位；
第1行第2列的数 = 50 表示将明文中的第50位的数放在第2位；
…
数组中，第i行第j列的数 = m 表示将明文中的第m-1位的数放到第(i*总列数+j)位（此处i，j都是0-index，但是m是1-index，为了对应到数组，使用m-1）。

//Unit.java
String handled_text = init_permutation(plain_text);

//Unit.java
private String init_permutation(String plain_text) {
    return op.permutation(plain_text, op.ip);
}

//Operation.java
public String permutation(String text, int[][] grid) {
    char[] tmpCharArray = text.toCharArray();
    int leni = grid.length;
    int lenj = grid[0].length;
    char[] resCharArray = new char[leni * lenj];
    for (int i = 0; i < leni; i++) {
        for (int j = 0; j < lenj; j++) {
            int index1 = i * lenj + j;
            int index2 = grid[i][j] - 1;
            resCharArray[index1] = tmpCharArray[index2];
        }
    }
    return new String(resCharArray);
}

.java说明：

Unit类包含对一个unit，即input block(64 bits)进行处理。
Operation类包含置换数组ip、置换操作permutation等基本数据和操作。显然，op是Operation的一个实例化对象。

0-2、16个子密钥（Ki）的生成

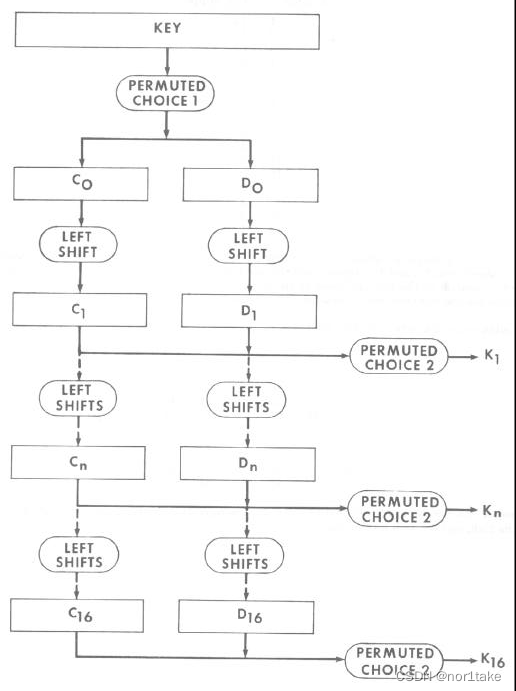
16个子密钥（Ki）的生成

输入：密钥（64 bits）
过程1：Permuted Choices 1（依然是一个置换操作）
中间量：处理后的密钥1（56 bits）
过程2：对处理后的密钥均分出来的C0、D0（28 bits）进行左移（注：每轮左移位数不同）
中间量：处理后的密钥2（56 bits） = C0’ + D0’
过程3：Permuted Choices 2（置换操作）
输出：子密钥1（48 bits）

//Operation.java
public int[][] pc1 = new int[][]{
        {57, 49, 41, 33, 25, 17, 9},
        {1, 58, 50, 42, 34, 26, 18},
        {10, 2, 59, 51, 43, 35, 27},
        {19, 11, 3, 60, 52, 44, 36},
        {63, 55, 47, 39, 31, 23, 15},
        {7, 62, 54, 46, 38, 30, 22},
        {14, 6, 61, 53, 45, 37, 29},
        {21, 13, 5, 28, 20, 12, 4}
};

public int[][] pc2 = new int[][]{
        {14, 17, 11, 24, 1, 5},
        {3, 28, 15, 6, 21, 10},
        {23, 19, 12, 4, 26, 8},
        {16, 7, 27, 20, 13, 2},
        {41, 52, 31, 37, 47, 55},
        {30, 40, 51, 45, 33, 48},
        {44, 49, 39, 56, 34, 53},
        {46, 42, 50, 36, 29, 32}
};

public int[] left_shift = new int[]{1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1};

置换操作为什么可以减少bit？

从数组PC-1（Permuted Choices 1）可以看出：数组中并没有8、16、…、64，说明：在生成output的时候，并没有选择input的第8位、第16位、…、第64位，自然就能做到减少bit。之后的拓展置换同理。

KEY的每8位中的1位用于密钥生成、分发和存储中的错误检测。第8，16，…，64位用于每个字节奇偶校验。

//Unit.java
subKey_generation();

//Unit.java
private void subKey_generation() {
    //1、PC-1 K(64) -> K'(56)
    String handled_secret_key = op.permutation(secret_key, op.pc1);

    //2、K'/2 = C, D(28)
    op.cut(handled_secret_key);
    String C = op.tmpL;
    String D = op.tmpR;

    int epoch = 0;
    while (epoch < 16) {
        //C, D左移
        for (int i = 0; i < op.left_shift[epoch]; i++) {
            C = op.shiftLeft(C);
            D = op.shiftLeft(D);
        }
        //PC-2 C+D(56) -> subKeys[i](48)
        subKeys[epoch] = op.permutation(C + D, op.pc2);
        epoch++;
    }
}

//Unit.java
//平分字符串（存入全局变量tmpL tmpR）
public void cut(String text) {
    int len = text.length();
    tmpL = text.substring(0, len / 2);
    tmpR = text.substring(len / 2);
}

//Unit.java
//不做“正负数左移补1还是0”的讨论，统一为：补第1位（即：第1位是0补0，第1位是1补1）
public String shiftLeft(String text) {
    return text.substring(1) + text.charAt(0);
}

1、加密过程（16轮）

现在，我们已经准备好：处理（Initial Permutation）后的明文 和 子密钥 Ki。

在第一轮加密中，处理后明文的右半部分R0和子密钥进行了一个f操作，得到f(R0, K1)，f(R0, K1)和L0异或得到下一轮的R1，即如图公式：R1 = L0 XOR f(R0, K1)。而新一轮的L1就是上一轮的R0。

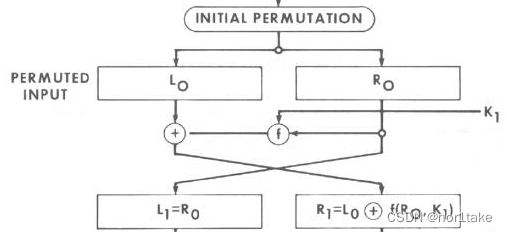
后面的每一轮都是重复上述过程：
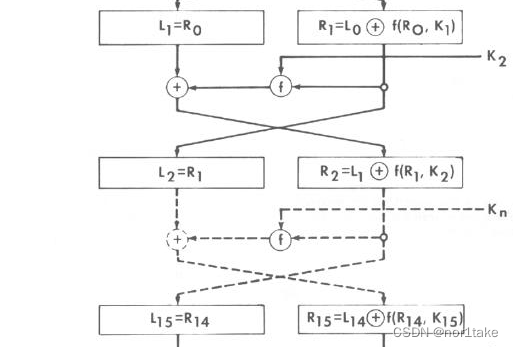
之后的每一轮

操作f的具体步骤：
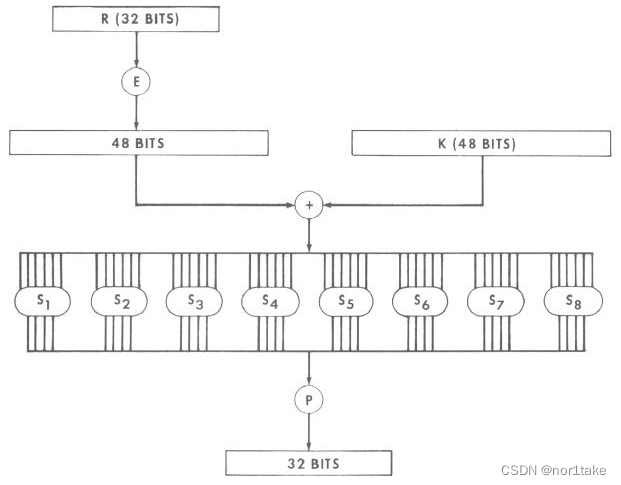
DES算法图中的操作f具体实现

输入：每轮处理后的明文的右边部分R（32 bits）
过程1：E（拓展置换）
中间量：R’（48 bits）+ 当前轮的子密钥 Ki（48 bits）
过程2：异或
中间量：M（48 bits）
过程3：S盒（input：M每6 bits对应一个Si操作；output：4 bits）
中间量：M’（32 bits）
过程4：P（置换）
输出：M’'（32 bits）

操作Si的具体步骤：

input（6 bits）的首尾 bit 构成一个二进制数，表示行i；
input（6 bits）的中间 4 bits 构成一个二进制数，表示列j
在数组Si中，找到Si[i][j]，并将其转化成 4 bits的二进制输出output

//Operation.java
//E置换
public int[][] extend = new int[][]{
        {32, 1, 2, 3, 4, 5},
        {4, 5, 6, 7, 8, 9},
        {8, 9, 10, 11, 12, 13},
        {12, 13, 14, 15, 16, 17},
        {16, 17, 18, 19, 20, 21},
        {20, 21, 22, 23, 24, 25},
        {24, 25, 26, 27, 28, 29},
        {28, 29, 30, 31, 32, 1}
};
//P置换
public int[][] p = new int[][]{
        {16, 7, 20, 21, 29, 12, 28, 17,},
        {1, 15, 23, 26, 5, 18, 31, 10,},
        {2, 8, 24, 14, 32, 27, 3, 9,},
        {19, 13, 30, 6, 22, 11, 4, 25},
};

//Si
public int[][] S1 = new int[][]{
        {14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7},
        {0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8},
        {4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0},
        {15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13}
};
public int[][] S2 = new int[][]{
        {15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10},
        {3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5},
        {0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15},
        {13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9}
};
public int[][] S3 = new int[][]{
        {10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8},
        {13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1},
        {13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7},
        {1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12}
};
public int[][] S4 = new int[][]{
        {7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15},
        {13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9},
        {10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4},
        {3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14}
};
public int[][] S5 = new int[][]{
        {2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9},
        {14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6},
        {4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14},
        {11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3}
};
public int[][] S6 = new int[][]{
        {12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11},
        {10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8},
        {9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6},
        {4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13}
};
public int[][] S7 = new int[][]{
        {4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1},
        {13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6},
        {1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2},
        {6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12}
};
public int[][] S8 = new int[][]{
        {13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7},
        {1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2},
        {7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8},
        {2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11}
};

//Unit.java
for (int i = 0; i < 16; i++) {
    iteration(L, R, i);
    L = op.tmpL;
    R = op.tmpR;
}

//Unit.java
private void iteration(String L0, String R0, int i) {
    //L1 = R0
    op.tmpL = R0;

    //操作f(R0, Ki)
    //f1：E置换：R0(32) -> (48)
    R0 = op.permutation(R0, op.extend);
    
    //f2：(48) = R0 ^ subKey[0]
    String Rtmp = op.XOR(R0, subKeys[i]);

    //f3：S盒：(48) -> (32)
    String tmp = op.sBox_permutation(Rtmp);

    //f4：P置换：(32)->(32)
    tmp = op.permutation(tmp, op.p);

    //R1 = L0 XOR f(R0, Ki)
    String R1 = op.XOR(L0, tmp);
    op.tmpR = R1;
}

//Operation.java
public String sBox_permutation(String x) {
    char[] xArray = x.toCharArray(); // (48)

    int index = 0;

    StringBuffer res = new StringBuffer();

    // 8 轮，每轮处理 6 bits。输入: 6；输出: 4
    for (int i = 0; i < 8; i++, index += 6) {
        // row = 6 bits 的 首尾 bit
        int row = (xArray[index] - '0') * 2 + (xArray[index + 5] - '0');

        // col = 6 bits 的 中间 4 bits
        int col = 0;
        for (int j = 1; j <= 4; j++) {
            col += (xArray[index + j] - '0') * Math.pow(2, 4 - j);
        }

        //在 Si 中定位一个整数
        int num = sBoxs.get(i)[row][col];
        res.append(binary[num]);
    }

    return res.toString();
}

2、最后一步

最后一步

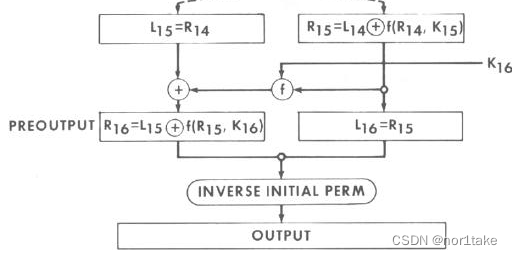
输入：pre-output = R16 + L16（注：不是L16 + R16）
过程：inverse initial perm（逆初识置换）
输出：密文

//Operation.java
public int[][] anti_ip = new int[][]{
        {40, 8, 48, 16, 56, 24, 64, 32},
        {39, 7, 47, 15, 55, 23, 63, 31},
        {38, 6, 46, 14, 54, 22, 62, 30},
        {37, 5, 45, 13, 53, 21, 61, 29},
        {36, 4, 44, 12, 52, 20, 60, 28},
        {35, 3, 43, 11, 51, 19, 59, 27},
        {34, 2, 42, 10, 50, 18, 58, 26},
        {33, 1, 41, 9, 49, 17, 57, 25}
};

//Unit.java
cipher_text = anti_permutation(R + L);

//Unit.java
private String anti_permutation(String s) {
    return op.permutation(s, op.anti_ip);
}

二、DES 解密

解密的第一个置换是IP，不是逆IP
for (int i = 15; i >= 0; i--) {}：从i=15开始，i--

//Unit.java
public void decryption(String cipher_text) {
    //0-1、初识置换：M(64) -> M'(64)
    String handled_text = init_permutation(cipher_text);
    
    //0-2、子密钥生成
    subKey_generation();

	//1、16轮加密
    op.cut(handled_text);
    String L = op.tmpL; // [0, 32)
    String R = op.tmpR; // [32:]
    for (int i = 15; i >= 0; i--) {
        iteration(L, R, i);
        L = op.tmpL;
        R = op.tmpR;
    }

    //2、逆置换
    plain_text = anti_permutation(R + L);
}