题目描述
给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数,要求从同一个数组中取出的数字保持其在原数组中的相对顺序。
求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。
说明: 请尽可能地优化你算法的时间和空间复杂度。
- 示例 1:
输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:
[9, 8, 6, 5, 3]
- 示例 2:
输入:
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
输出:
[6, 7, 6, 0, 4]
- 示例 3:
输入:
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
输出:
[9, 8, 9]
思路分析
整体思路:假设 arr1 中有10个数,arr2 中有8个数,而
k
=
5
k=5
k=5,那么有如下几种可能性:
- 5个数全部来自arr1,arr2中的数不需要,如何选择才能最大;
- 4个数来自arr1,1个数来自arr2,如何merge才能最大;
- 3个数来自arr1,2个数来自arr2,如何merge才能最大;
- 2个数来自arr1,3个数来自arr2,如何merge才能最大;
- 1个数来自arr1,4个数来自arr2,如何merge才能最大;
- 0个数来自arr1,5个数全部来自arr2,如何选择才能最大。
最终结果就是所有可能性中的最大值。
于是需要解决两个问题:
- 在一个数组中从左往右挑 m m m 个数,怎么挑选才能使得其尽量大?
- 从两个数组中挑选出来的数怎么merge才能最大?
解决问题1:在一个数组中从左往右挑 m m m 个数,怎么挑选才能使得其尽量大?
因为要在数组中可能挑不同数量的数多次,所以要先解决一个批量查询的问题,先预处理一个结构,之后不管是在数组挑几个数,从这个预处理结构中都能很快得到答案,也就是说「解决批量查询,做一个预处理结构」。
准备一张 dp 表,行表示数组的下标,列表示个数,定义 dp[i][j] 表示只能从arr数组的
i
i
i 位置及其往后的位置中挑选
j
j
j 个数,最大结果的开始位置。
比如数组 [6, 7, 4, 9, 2],dp[2][1] = 3,因为从数组2位置下标开始只能选1个数,最大的就是3位置的9,所以 dp[2][1] = 3。
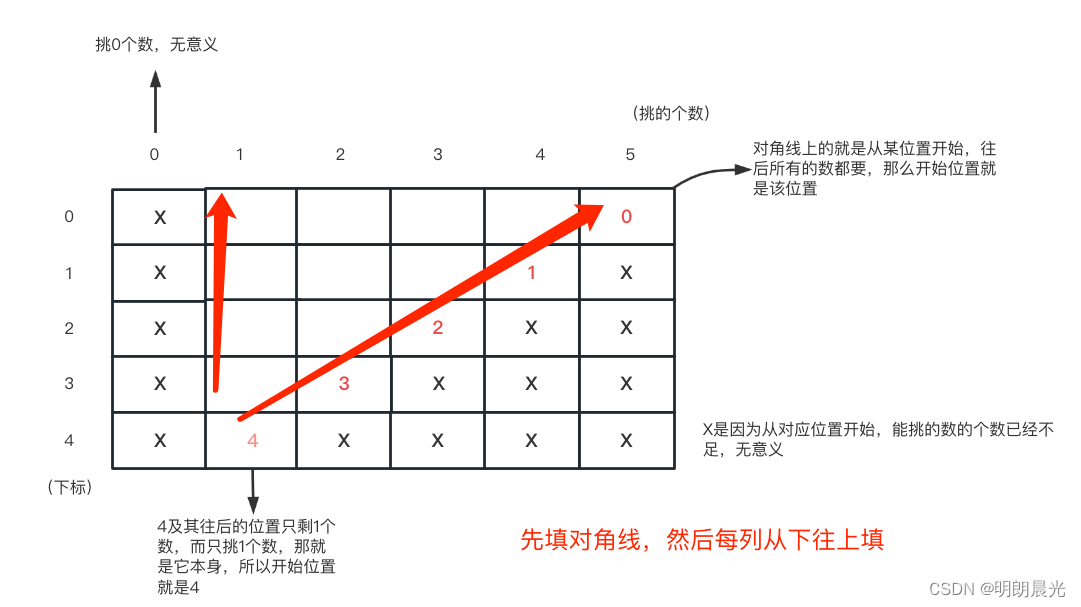
按照填表规则“先填对角线,然后从左往右,每列从下往上填”,那么当要填 dp[i][j] 时,dp[i+1][j] 是已经填好的了,如何使用 dp[i+1][j] 指导 dp[i][j] 的填写?
假设现在要填 dp[7][3],则之前 dp[8][3] 已经填写过,若dp[8][3] = 13,那么只需要比较 7 位置的数和 13 位置的数,如果arr[7] > arr[13],则dp[7][3] = 7;如果 arr[7] < arr[13],则 dp[7][3] = 13。关键是如果 arr[7] = arr[13],应该怎么处理?注意相等的时候一定要选7,即dp[7][3] = 7,虽然相等情况下,第一个数无论是7位置还是13位置都是相同的,但是选择7位置开始后,可以让接下来的第二个数也尽量好。
举个例子:假如从8位置开始往后选3个数,得到的最大结果是996,而因为7位置的数和13位置是相同的,所以7位置的数也是9,那么从7位置选三个数,可以得到999,即13位置的9变成了第二个9。所以当7位置的数和13位置的数相同的时候,一定要选择7位置的数,这样会使得后面的结果潜在地变好。
填第1列:

补充填完整个表:

这张表就是预处理结构,可以获得数组arr中挑任意个数,怎么挑最大。
比如「如果要在数组 arr 中挑 2 个数,如何选择使得拼接的结果最大?」
根据表中信息已经知道「从0位置出发挑2个数」最好的开始位置是1,所以arr[1] = 9 要选择;然后问题就变成了「从2位置出发挑1个数」,而根据表中信息,dp[2][1] = 3,所以arr[3] = 9要选择。因此,最后「arr中挑2个数拼接的最大结果为99」。
这个预处理结构可以处理任意情况,比如 『要在 arr 中挑选 6 个数,怎么挑最大?』,其实质就是将问题分解成了如下步骤:
- 从0开始挑6个数的最开始位置,假设为7,则第一个要选择的数就是 arr[7];
- 然后问题变成了从 8 位置开始挑 5 个数的最开始位置,假设为13,则第二个要选择的数就是 arr[13];
- 然后问题变成了从 14 位置开始挑 4 个数的最开始位置,假设为19,则第三个要选择的数就是 arr[19];
- 然后问题变成了从 20 位置开始挑 3 个数的最开始位置,假设为25,则第四个要选择的数就是 arr[25];
- 然后问题变成了从 26 位置开始挑 2 个数的最开始位置,假设为30,则第五个要选择的数就是 arr[30];
- 以此类推,这些信息都可以在表中获得。
如果要在数组中选 m m m 个数,只需要在表中跳转 m m m 次,时间复杂度为 O ( m ) O(m) O(m)。
解决问题2:从两个数组中挑选出来的数怎么merge才能最大?
【没有优化的merge方法】
假设 k = 8 k=8 k=8,已经从两个数组中分别将数挑选出来:[9, 9, 9, 3, 2],[9, 9, 4]
一开始,准备两个指针,各自指向数组的开头,如下:
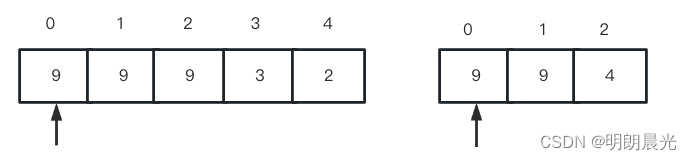
依次比较两个数组中的值,直到比较出大小。即:
- arr1[0] = arr2[0],没有分出大小,继续比较后一个位置;
- arr1[1] = arr2[1],没有分出大小,继续比较后一个位置;
- arr1[2] > arr2[2],分出了大小。
于是将arr1中此时指针指向的9作为答案的第一位:
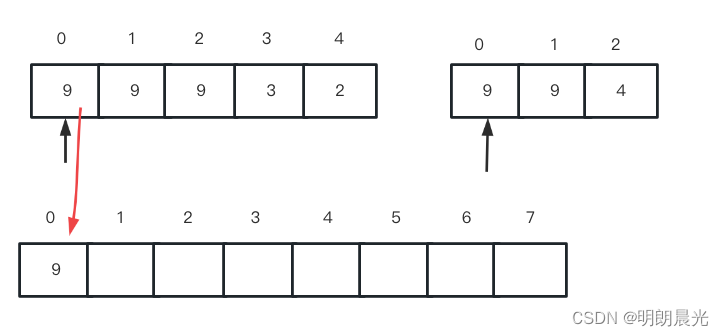
然后 arr1 的指针后移一位:

继续依次比较,直到分出大小,即:
- arr1[1] = arr2[0],没分出大小,继续比较后一个位置;
- arr1[2] = arr2[1],没分出大小,继续比较;
- arr1[3] < arr2[2],分出大小。
于是选择arr2此时指针指向的9 作为结果的第二位:
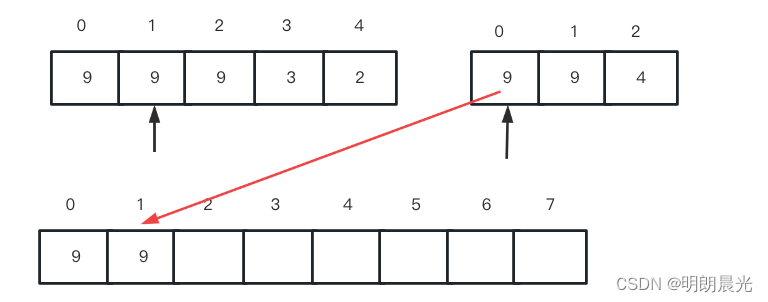
然后 arr2 的指针后移:
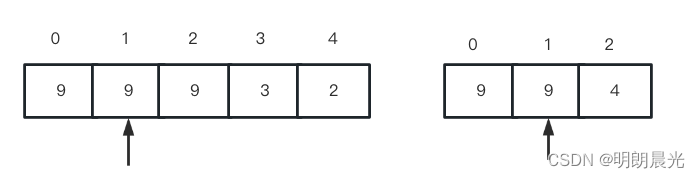
继续重复从指针开始的位置依次比较的操作,直到分出大小。
总结来说就是从两个数组指针指向的位置的值相等时,必须依次比较,直到比较出大小,然后取较大的那个值所在数组中当前指针指向的值,然后将该数组的指针后移。这个操作的时间复杂度是平方规模的。
注意,在相等时不能随意选一个,而是必须像上述操作一样,依次比较直到区分出大小为止。比如 [5, 9] 和 [5, 6] 合并,一开始两个数组的第一个位置相等,如果直接选择了第二个数组的5,那么最终得到的结果是 5659 而不是正确的 5956。
【优化过的merge方法】
上述的操作中,其实就是在找两个数组当前指针所指向的位置开始的后缀串的字典序,比较这两个字典序的大小,取字典序较大的数组中当前指针指向的值。
而此前已经将两个数组合并为一个数组利用DC3算法求出了后缀数组,所以两个数组当前指针指向的位置的字典序大小根据后缀数组能很轻易地得到。
举个例子来说明整体流程:arr1 = [3, 1, 2, 6], arr2 = [6, 9],两个数组中的每个值都+2,然后用1隔开,则合并成一个数组是 [5, 3, 4, 8, 1, 9, 11],将该数组利用DC3算法求出后缀数组,然后比较原数组对应到该合成数组中的下标位置,利用字典序的大小进行合并。
代码实现
// 测试链接: https://leetcode.com/problems/create-maximum-number/
public class CreateMaximumNumber {
public static int[] maxNumber1(int[] nums1, int[] nums2, int k) {
int len1 = nums1.length;
int len2 = nums2.length;
if (k < 0 || k > len1 + len2) {
return null;
}
int[] res = new int[k];
int[][] dp1 = getdp(nums1); // 生成dp1这个表,以后从nums1中,只要固定拿N个数,
int[][] dp2 = getdp(nums2);
// get1表示从arr1里拿的数量
// K - get1表示从arr2里拿的数量
// 如果arr1中有10个数,arr2中有8个数,而k=5,则可以依据前文的方案枚举可能性:
// ① arr1 选5个,arr2选0个;
// ② arr1 选4个,arr2选1个;
// ③ arr1 选3个,arr2选2个;
// ④ arr1 选2个,arr2选3个;
// ⑤ arr1 选1个,arr2选4个;
// ⑥ arr1 选0个,arr2选5个。
// 但是如果 arr1 中只有4个数,arr2中只有3个数,而k=5,则需要根据这几个值的关系定制方案:
// ① arr1 选4个,arr2 选1个;
// ② arr1 选3个,arr2 选2个;
// ③ arr1 选2个,arr2 选3个;
//如果arr1中有 N 个数,arr2中有 M 个数,选择 K 个数
//若M < K,则在arr1中至少要选择K-M个数,而 M>=K 的时候,在arr1中最少可以选择0个
// 若N < K,则在arr1中最多选择N个数;若N >= K, 在arr1中最多选择K个数
//所以在arr1中可以挑选的数的个数范围为 [max{0, K-M}, min{K, N}]
for (int get1 = Math.max(0, k - len2); get1 <= Math.min(k, len1); get1++) {
int[] pick1 = maxPick(nums1, dp1, get1); // arr1 挑 get1个,怎么得到一个最优结果
int[] pick2 = maxPick(nums2, dp2, k - get1); //arr2 挑 k-get1个,怎么得到一个最优结果
int[] merge = merge(pick1, pick2); //从arr1和arr2中挑选出来的数怎么合并结果最优
res = preMoreThanLast(res, 0, merge, 0) ? res : merge;
}
return res;
}
//没有优化的merge
public static int[] merge(int[] nums1, int[] nums2) {
int k = nums1.length + nums2.length;
int[] ans = new int[k];
for (int i = 0, j = 0, r = 0; r < k; ++r) {
ans[r] = preMoreThanLast(nums1, i, nums2, j) ? nums1[i++] : nums2[j++];
}
return ans;
}
public static boolean preMoreThanLast(int[] nums1, int i, int[] nums2, int j) {
while (i < nums1.length && j < nums2.length && nums1[i] == nums2[j]) {
i++;
j++;
}
return j == nums2.length || (i < nums1.length && nums1[i] > nums2[j]);
}
public static int[] maxNumber2(int[] nums1, int[] nums2, int k) {
int len1 = nums1.length;
int len2 = nums2.length;
if (k < 0 || k > len1 + len2) {
return null;
}
int[] res = new int[k];
int[][] dp1 = getdp(nums1);
int[][] dp2 = getdp(nums2);
for (int get1 = Math.max(0, k - len2); get1 <= Math.min(k, len1); get1++) {
int[] pick1 = maxPick(nums1, dp1, get1);
int[] pick2 = maxPick(nums2, dp2, k - get1);
int[] merge = mergeBySuffixArray(pick1, pick2);
res = moreThan(res, merge) ? res : merge;
}
return res;
}
public static boolean moreThan(int[] pre, int[] last) {
int i = 0;
int j = 0;
while (i < pre.length && j < last.length && pre[i] == last[j]) {
i++;
j++;
}
return j == last.length || (i < pre.length && pre[i] > last[j]);
}
//优化版本的merge
public static int[] mergeBySuffixArray(int[] nums1, int[] nums2) {
int size1 = nums1.length;
int size2 = nums2.length;
int[] nums = new int[size1 + 1 + size2]; //合并成一个数组
for (int i = 0; i < size1; i++) {
nums[i] = nums1[i] + 2;
}
nums[size1] = 1;
for (int j = 0; j < size2; j++) {
nums[j + size1 + 1] = nums2[j] + 2;
}
DC3 dc3 = new DC3(nums, 11);
int[] rank = dc3.rank;
int[] ans = new int[size1 + size2];
int i = 0;
int j = 0;
int r = 0;
while (i < size1 && j < size2) {
//通过rank数组能直接知道哪个字典序更大
ans[r++] = rank[i] > rank[j + size1 + 1] ? nums1[i++] : nums2[j++];
}
while (i < size1) {
ans[r++] = nums1[i++];
}
while (j < size2) {
ans[r++] = nums2[j++];
}
return ans;
}
public static class DC3 {
public int[] sa;
public int[] rank;
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank = rank();
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) {
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
private int[] rank() {
int n = sa.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[sa[i]] = i;
}
return ans;
}
}
public static int[][] getdp(int[] arr) {
int size = arr.length; // 0~N-1
int pick = arr.length + 1; // 1 ~ N
int[][] dp = new int[size][pick];
// get 不从0开始,因为拿0个无意义
for (int get = 1; get < pick; get++) { // 1 ~ N
int maxIndex = size - get;
// i~N-1
for (int i = size - get; i >= 0; i--) {
if (arr[i] >= arr[maxIndex]) {
maxIndex = i;
}
dp[i][get] = maxIndex;
}
}
return dp;
}
public static int[] maxPick(int[] arr, int[][] dp, int pick) {
int[] res = new int[pick];
for (int resIndex = 0, dpRow = 0; pick > 0; pick--, resIndex++) {
res[resIndex] = arr[dp[dpRow][pick]];
dpRow = dp[dpRow][pick] + 1;
}
return res;
}
}