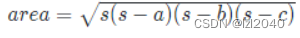前言:首先,这是不是你所了解的双指针算法?
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
...
}
}那你就要继续往下看了,双指针算法可不是简单的两层的for循环暴力,这并不能起到时间优化的作用。
那话不多说,我们马上开始~~~

目录
1.双指针思想
2.双指针思想的应用
2.1快慢指针编辑
双指针思路模板
2.2左右指针
3.金句省身
1.双指针思想
严格来说,双指针不是一种具体算法,而是一种思想,类似于贪心思想,双指针的技巧主要分为两类:快慢指针和左右指针。所谓左右指针,就是两个指针相向而行或相背而行,而快慢指针就是两个指针同向行走但是一快一慢。类似的例子有很多,比如二分算法,快排和归并排序等都利用了双指针算法。
在数组和链表中都可以采用双指针算法,本文重点来讲解在数组条件下使用双指针算法。
回到我们开头给出的代码,
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
...
}
}这是一个O(n^2)的算法,而我们如果采用双指针算法,可以将上面的算法优化到O(n),我们一起来看看如何实现的:
我们可以让第二个指针在某个特定的条件下移动的次数小于n次,那么我们的代码就可以变成:
for (int i = 0; i < n; i++)
{
while(j<n&&check(i,j))j++;//
...
}这样以来内外层每次循环的次数就会小于2*n,也就是复杂度就会下降到O(n)。
2.双指针思想的应用
2.1快慢指针
乍一看题目比较简单,我们可以定义两个指针,第一个指向起点,第二个指向终点,判断这个区间,满足就更新最大值,否则就将起点移动到下一位,继续找终点,直到找完为止。
我们不难给出代码:这里我用的STL做的,主要用于判重
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int a[maxn];
int mp[maxn];//表示数字的出现次数
int n;
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
}
int ans = 1;
for (int i = 0; i < n; i++)
{
int j = i;
while (mp[a[j]] < 1 && j < n)
{
mp[a[j]]++;
j++;
}
//printf("%d %d\n", i, j);
memset(mp, 0, sizeof(mp));
ans = max(ans, j - i);
}
printf("%d\n", ans);
return 0;
}
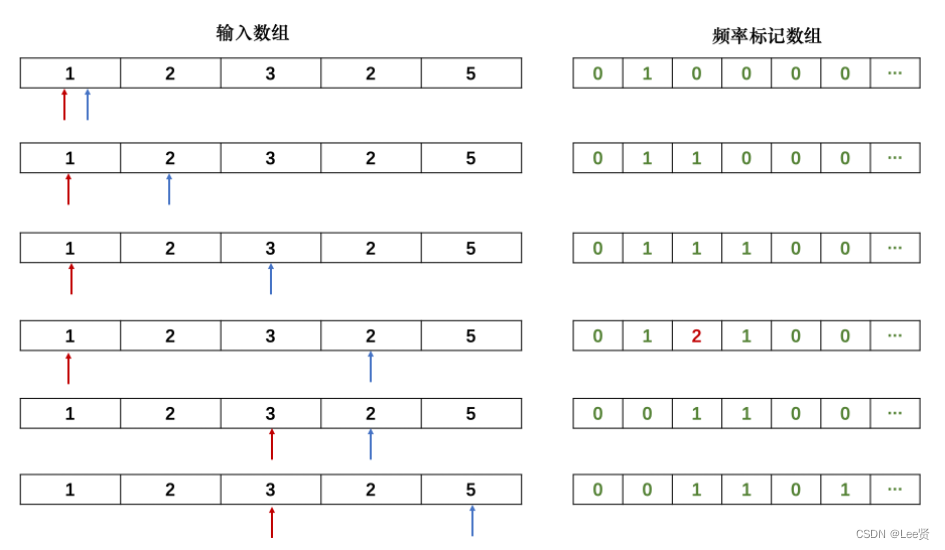
但是如果给我们十万个数据,代码就要TLE了,具体的原因可以看下面的图:

所以我们果断采用第二种实现方式,还是采用第一种空间换时间的做法,我们开一个记录当前数字个数的数组,然后确定一个终点,并从[0,i](i设为终点)中从左侧选择起点j,如果此时选择的,就一定是由于起点导致出现了重复元素,我们就让起点向终点移动,至于为什么一定是起点的问题,因为我们的终点就是从0一点点枚举变大的,所以我们在枚举出第i个符合条件的起点时,第i-1个起点已经求出并涵盖在和第i个起点内,所以一定是区间最外层的节点导致重复现象的产生。
那么这里便给出代码,对应可以理解下:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int a[maxn];
int mp[maxn];//表示数字的出现次数
int n;
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
}
int ans = 1;
for (int i = 0,j=0; i < n; i++)//i指向终点,j指向起点
{
//首先终点要加入
mp[a[i]]++;
while (mp[a[i]] > 1 && j <= i) //只要是我们的a[i]出现的次数还大于1,就说明中间出现了至少一次终点的元素值,我们的起点j就需要找到这个点为止,这里由于i一定大于等于j,所以第二个条件可有可无
--mp[a[j++]];//注意是先减再j++
ans = max(ans, i - j + 1);
}
printf("%d\n", ans);
return 0;
}
这里我们就总结给出双指针思想的一般模板思路:
双指针思路模板
for (int i = 0, j = 0; i < n; i++)
{
//...前置条件
while (j < i && check(j, i)) j++;//这可以将原O(n*n)的算法优化成O(n)
...//每道题目的具体逻辑
}2.2左右指针
我们常见的二分法就是左右指针的经典应用,这里不在赘述,详见:http://t.csdn.cn/LWFvP
3.金句省身
你一定要狠下心来努力,努力变成一个很厉害的人,没有必要让别人知道你的计划,退出不合适的圈子和不合适的人,断开不如意的感情,做最真实的自己。要成为那种不声不响,却什么都做得很好的人,早睡早起,坚持锻炼,沉下心来学习,相信点滴的努力都会有意义,努力追上那个曾将被赋予厚望的自己。