归并排序

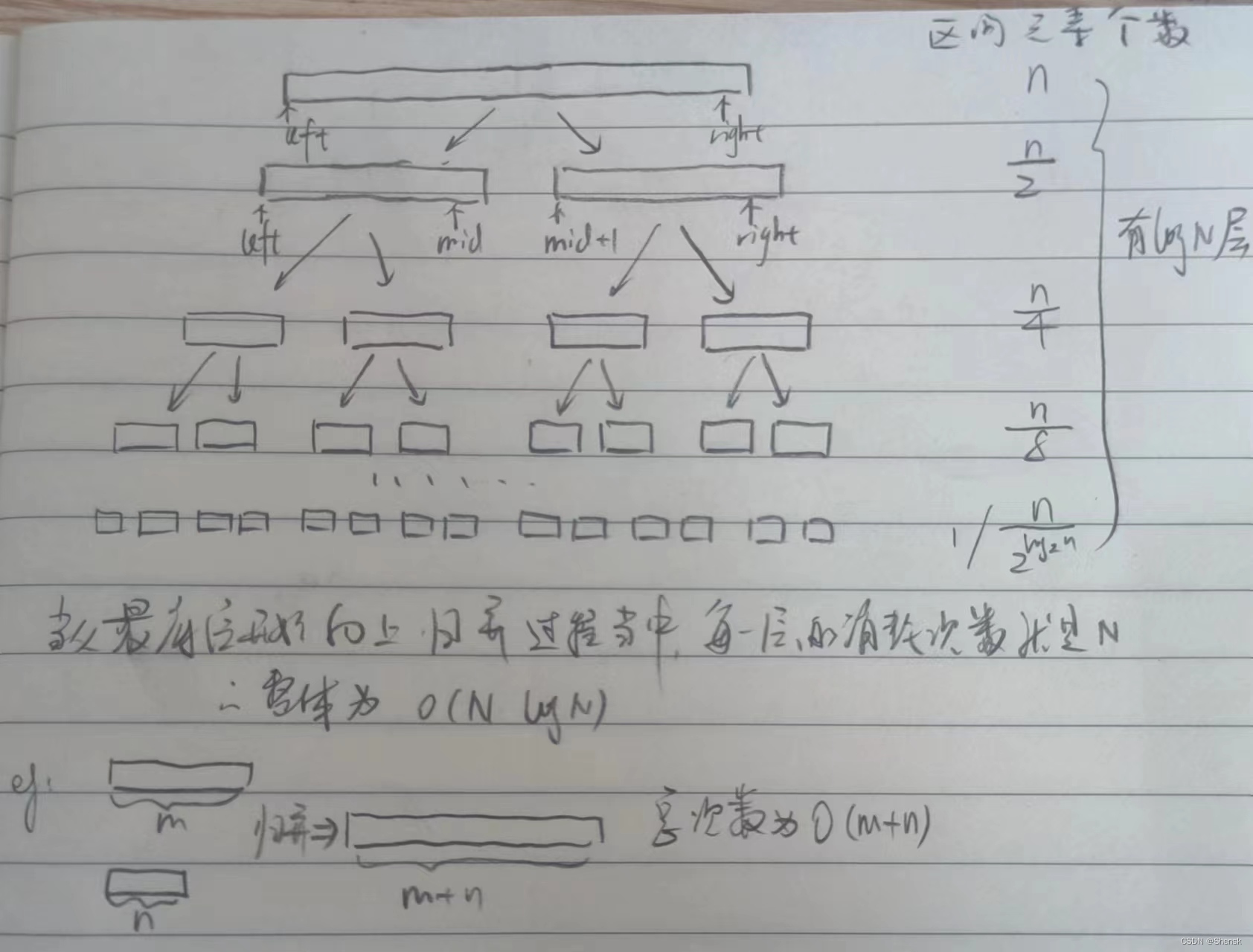
1. 归并排序采用的是两个有序数组的归并。比如说现在想让一个数组有序。之前我们讲过，如果说你现在有两个有序数组的话，那么我们就可以把这两个有序数组给他合并成一个有序数组。
2. 两个有序区间归并的思路其实很简单（这个也是归并的单趟排序）：就是把这两个有序区间从开头一直向后面，依次比较，小的尾插到新空间，是新空间。像链表用归并这个思想的话，他可以把那个节点给他“摘”下来，然后改动一下链接关系；但是如果对于数组要用归并思想的话，必须得借助一个新的空间。因此必须得归并到一个新数组。这个就是归并的过程
   整个归并排序的归并过程其实可以生动想象成：
   1. 首先tmp临时作坊得接收客户的两批原料，当然这两批原料必须得是合格的（就是说两个区间必须是各自有序的）
   2. 然后tmp临时作坊依托这两种原料在作坊里面制成了产品（把两个有序区间归并成的一个有序区间）
   3. 然后这种产品造出来后在要交付出去（也就是说给他拷贝到原先的arr数组当中）
   4. 客户不满意说我要更大的产品，就把原先产品退回来当原料造更大的（不断向上归并）
3. 上面讲的这种归并的思想，它是建立在一个前提之上。就是首先得有两个有序的区间。比如说左区间有序加上右区间有序。那我现在没有有序呢？乱的呢？
4. 那该怎么让左右子区间有序呢？这边采用一个分治的方法。比如说我现在想要让八个数有序，那我就先给他分成四个数，四个数，然后到时候再进行归并。然后如果说这四个数是有序的话那还好，可以直接拿来进行归并，如果说没有序的话，接下来看这个四个数的这么一个整体，我现在想让这四个数有序，那么我就给他分成两个数，两个数；然后如果说这两个数是有序的话，那么还好，就可以直接拿来进行归并，如果说这两个数是无序的话，那么就再给他分成一个数，一个数。那一个数肯定是有序的了对吧，然后一个数一个数就可以给他归并成两个；然后两个数，两个数就可以归并成四个；然后四个数，四个数就可以给他归并成八个。
   
5. 在归并的过程当中，必须得确保左右子区间两个都是有序的情况之下，然后才可以向上进行归并。那既然必须得确保左右两个子区间都是有序的，你必须得认识到，你肉眼看他，好像诶都已经有序了，但实际上计算机怎么知道它有序？因此你在归并递归的过程当中，必须一直深入到最后一层：也就是说每一个区间相当于只有一个数了，那这时候计算机他才知道哦这下子每一个区间都已经有序了，然后可以归并了。
   再来重复一下： 整个归并排序的归并过程其实可以生动想象成：
   1. 首先tmp临时作坊得接收客户的两批原料，当然这两批原料必须得是合格的（就是说两个区间必须是各自有序的）
   2. 然后tmp临时作坊依托这两种原料在作坊里面制成了产品（把两个有序区间归并成的一个有序区间）
   3. 然后这种产品造出来后在要交付出去（也就是说给他拷贝到原先的arr数组当中）
   4. 客户不满意说我要更大的产品，就把原先产品退回来当原料造更大的（不断向上归并）

归并排序代码实现

1. 在归并排序当中，首先得开一个临时数组。这个临时数据的作用好比较是将原料拿过来在我数组内部做成产品然后再把整个制成品放到市场。
2. 在归并排序的话，并不是去递归mergesort函数，而是去写一个子函数，然后去递归子函数_MergeSort
3. 这个_MergeSort函数的功能在于把arr数组当中left-right之间区间里面的数字给他排成有序的。
4. 首先因为我需要去平分一下左右区间，所以先要计算出mid，然后给他分成两个区间begin-mid，mid+1-end。
5. 然后对这两个区间进行两个递归。至于到底是怎么有序的，先不用去管，反正当对这两个区间进行两次递归操作之后，这两个区间现在已经是各自有序的了。
6. 然后就是进行归并。因为现在已经有两个有序区间了，对于这两个有序区间用begin1, end1, begin2, end2进行维护。然后归并就不讲了看代码。
7. 当归并完了之后，现在的产品还在tmp数组里面，那么现在就要给他拷贝到原先的arr数组里面，用memcpy即可。
8. ***归并的时候没有规定两个有序数组的数据必须个数一样，跟个数没有关系。***并没有说必须得对称。
9. 
10. 再来重复一下： 整个归并排序的归并过程其实可以生动想象成：
    1. 首先tmp临时作坊得接收客户的两批原料，当然这两批原料必须得是合格的（就是说两个区间必须是各自有序的）
    2. 然后tmp临时作坊依托这两种原料在作坊里面制成了产品（把两个有序区间归并成的一个有序区间）
    3. 然后这种产品造出来后在要交付出去（也就是说给他拷贝到原先的arr数组当中）
    4. 客户不满意说我要更大的产品，就把原先产品退回来当原料造更大的（不断向上归并）

void _MergeSort(int* arr, int left, int right, int* tmp)
{
	if (left >= right)
	{
		return;
	}
	int mid = (left + right) / 2;
	_MergeSort(arr, left, mid, tmp);
	_MergeSort(arr, mid + 1, right, tmp);
	int begin1 = left;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = right;
	int k = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] < arr[begin2])
		{
			tmp[k++] = arr[begin1++];
		}
		else
		{
			tmp[k++] = arr[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[k++] = arr[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[k++] = arr[begin2++];
	}
	memcpy(arr + left, tmp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* arr, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc failed");
		return;
	}
	_MergeSort(arr, 0, n - 1, tmp);
	free(tmp);
}

归并排序的时间复杂度

1. 归并排序时间复杂度：对于快速排序而言的话，它实际上还要更复杂一点，因为他必须得依赖并且考虑到在单趟排序完成之后这个key的位置。因此你把地柜展开的话，它并不一定是一个满二叉树。把这边的归并排序的话，就是每一次的平分。
2. 首先的话，它整个的高度是logN。对于分割来说，不需要消耗就直接分割O(1)。
3. 真正的消耗在于归并。当比如说把两段有序的区间（长度为m,n）给他归并成一个区间的时候，这时候总的消耗就是O(m+n)，然后你会发现每一层的归并的消耗都是n，那么整体就是NlogN。
4.