前言

答应大家的计数排序今天它来了，这也是一个非常巧妙的方法，不通过比较元素的大小就可以排序出来，通过用另一个人数组的下标来表示原数组里面的元素的值，然后通过此数出现的个数进行排序

一、计数排序

我们来看图解：
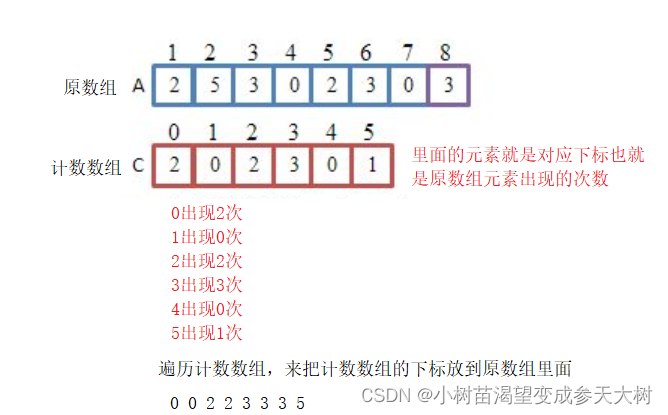
在这里插入图片描述

目前我们要解决的问题就是计数数组的大小怎么确定，既然计数数组的下标是原数组里面的值，那开的数组的大小最小为原数组中最大元素大小加一，例如上面实例，最大值为5，我们就要开6个大小的空间。

我们来看计数排序的代码：

void CountSort2(int* a, int n)
{
	
	int max = 0;
	for (int i = 0; i < n; i++)//找出最大值和最小值
	{
		if (a[i] >= a[max])
		{
			max = i;
		}
	}
	int count = a[max] + 1;
	int* tmp = (int*)malloc(sizeof(int) * count);//开辟范围差数组
	memset(tmp, 0, sizeof(int) * count);//将开辟的计数数组赋值为0
	for (int i = 0; i < n; i++)//计数，
	{
		tmp[a[i]]++;
	}
	int j = 0;
	for (int i = 0; i < count; i++)//排序
	{
		while (tmp[i]--)
		{
			a[j++] = i;
		}
	}
}

我们来看运行结果：
在这里插入图片描述

但是这个代码有一个不好的地方，但数据出现最大数和最小数都很大很大的时候，例如：90，93，100，1001
那这个时候我们开辟的计数数组就太大的，浪费了，所以我们就要想一个办法，我们可以开辟一个范围大小，下标就表示原数组的元素减最小数的大小
我们再来看改进的计数排序：

void CountSort1(int* a, int n)
{
	int min = 0;
	int max = 0;
	for (int i = 0; i < n; i++)//找出最大值和最小值
	{
		if (a[i] <= a[min])
		{
			min = i;
		}
		if (a[i] >= a[max])
		{
			max = i;
		}
	}
	int count = a[max] - a[min] + 1;
	int* tmp = (int*)malloc(sizeof(int) * count);//开辟范围差数组
	memset(tmp, 0, sizeof(int) * count);
	for (int i = 0; i < n; i++)//计数，
	{
		tmp[a[i] - min]++;
	}
	int j = 0;
	for (int i = 0; i < count; i++)//排序
	{
		while (tmp[i]--)
		{
			a[j++] = i + min;
		}
	}
}

看运行结果：
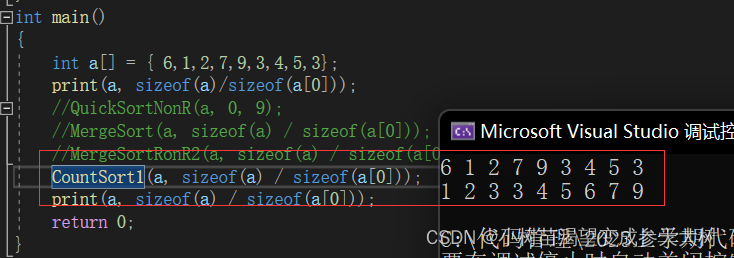
在这里插入图片描述
但是还是有不好的地方，当最大数和最小数差距很大，并且中间数据很少的时候，例如1，3，5，1000
这个时候计数排序就不是很友好，这个没有办法解决，这也是计数排序的缺点，所以计数排序适合数比较集中的排序。

计数排序的特性总结：

计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
时间复杂度：O(MAX(N,范围))
空间复杂度：O(范围)
稳定性：稳定

二、排序算法复杂度及稳定性分析

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
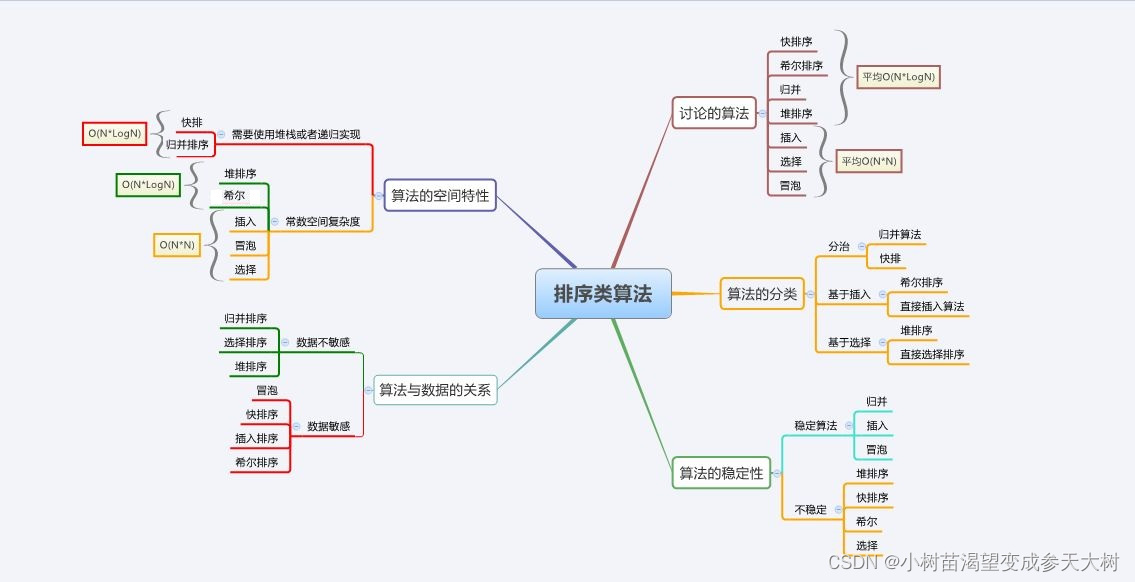
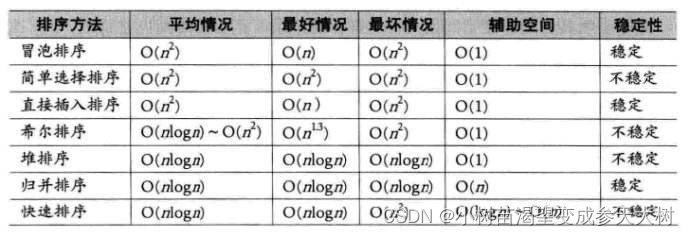
在这里插入图片描述

大家可以看看我之前排序的博客，来看看是否稳定。这里我就不在一一分析了。大家记住结论就行了。