【LeetCode】剑指 Offer 54. 二叉搜索树的第k大节点 p269 -- Java Version

news2025/10/31 4:47:36

题目链接：https://leetcode.cn/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/

1. 题目介绍（ 54. 二叉搜索树的第k大节点）

给定一棵二叉搜索树，请找出其中第 k 大的节点的值。

【测试用例】：
示例 1:
在这里插入图片描述
示例2：

【条件约束】：

限制：

1 ≤ k ≤ 二叉搜索树元素个数

2. 题解

2.1 中序遍历 – O(n)

时间复杂度O(n)，空间复杂度O(1)
在这里插入图片描述

【解题思路】：
由于题目给的树是 二叉搜索树 ，即具有以下性质：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树。

……
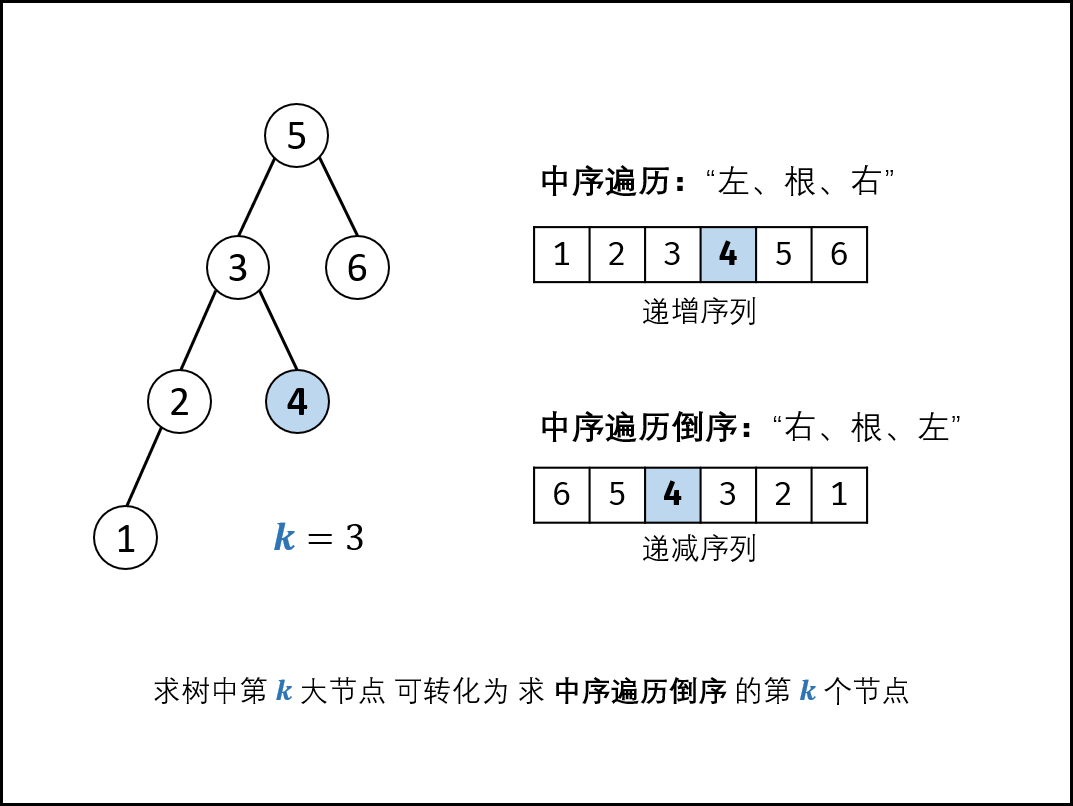
因此，若对它进行中序遍历，则是一颗递增的排好序的序列！

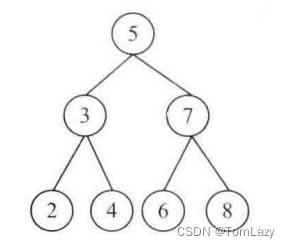
如上图所示，这是一棵有7个节点的二叉搜索树，它的中序遍历序列为 {2，3，4，5，6，7，8}
……
该题要求我们求的是一棵二叉搜索树的 第 k 大节点，那么就应该对应着中序遍历序列的 倒数第 k 个节点；以上面的二叉搜索树为例，第 1 大节点应为 8，第 2 大节点应为 7，依次类推，原书中的举例应该是错的，它说按节点数值大小顺序，第3大节点的值是4（感觉这里应该是说错了）
……
【实现策略】：
思路理清了，我们就可以愉快的写代码了
中序倒序遍历（右、根、左）求 第 k 大，同理，中序正序遍历（左、根、右）可以用来求 第 k 小

判断无效输入：头节点是否为空，k是否小于等于0；
以递归的形式 dfs() 来进行中序倒叙遍历，按照（右、根、左）的顺序；
定义一个全局的计数变量 idx，用来确认当前节点是否已经到了第 k 大节点，如果是，则将值保存在 res 中；(这里进一步简化的话，可以省略掉 idx 变量，转而直接操作 k ，让 k--，当 k 减至 0 时，代表已找到目标节点，无需再继续遍历)
递归结束，返回 res .

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    // Solution1：中序遍历
    int res,idx = 0;
    public int kthLargest(TreeNode root, int k) {
        // 无效输入判断
        if (root == null || k <= 0) return -1;
        // 递归中序遍历
        dfs(root,k);
        // 最后返回结果
        return res;
    }
    void dfs(TreeNode root, int k) {
        // 递归终止条件
        if(root == null) return;
        // 中序倒序遍历，找最大
        dfs(root.right,k);
        idx++;
        // 如果当前是第k大，赋值给res
        if(idx == k) res = root.val;
        // 找左子树
        dfs(root.left,k);
    }
}