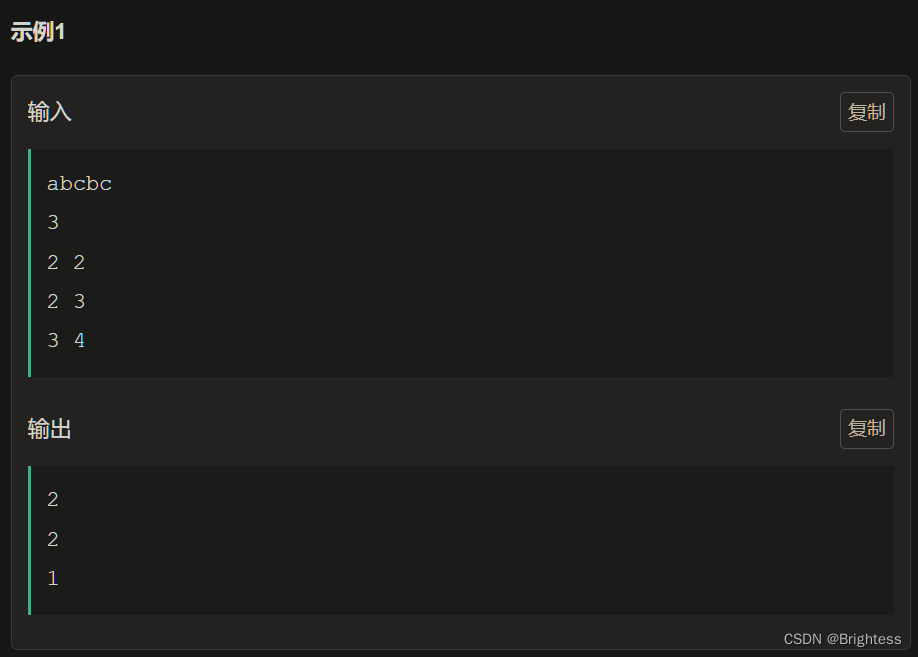
题意:
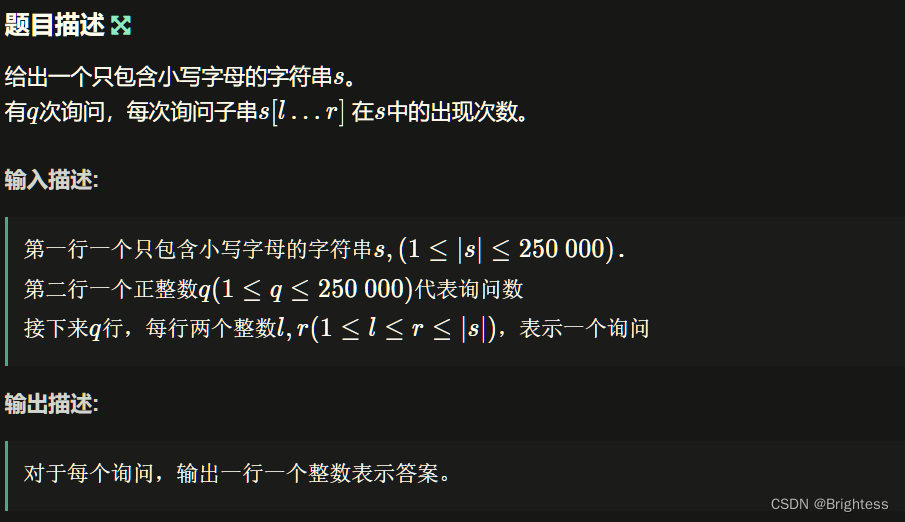
给出一个字符串S,|S| ≤ 250000,给出 Q < 250000 次询问,每次需要回答 S[l, r] 在 S 中共出现了多少次。
思路:
如果使用 SAM,我们提前求出每个状态的 cnt[u],询问就是要求我们快速定位 S[l, r] 所在的状态。
我们知道 S[l, r] 一定是 S 的前缀 S[1, r] 的后缀,而 S 的前缀共有 n 个:我们容易找到 S 的每个前缀对应的 SAM 状态节点,不妨设 S[1, i] 对应于状态 ed[i]。
由于 S[l, r] 是 S[l, r] 的后缀,他对应的状态一定位于 ed[i] 的后缀链接上,也即我们要从 ed[i] 到根 root 这条树链上最浅(也就是离根最近,子串结束位置最多,囊括了 S[l, r] 所有结束位置,等价于出现次数)的满足 len[u] >= r - l + 1 的状态。
显然暴力是会超时的,使用树上倍增即可,这里我们使用 dfs 预处理树上倍增要用的 pa 数组。
代码:
ask 函数中 if 里的判断我一开始还联系了节点代表子串长度的最小值 mnl,我写的是:
if(mxl >= leng && mnl <= leng),
这样是不行的,举个例子,比如下面的情况:
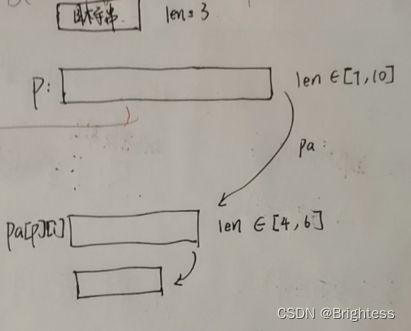
如果像我那样写,图中的第一个链就跳不了了,答案就会出错。
这就属于对倍增的理解不够透彻了,倍增的含义是:从大到小能跳就跳。
因此只需要考虑节点代表子串长度的最大值 mxl 和目标子串长度 leng 即可。
#include<bits/stdc++.h>
using namespace std;
const int N = 2.5e5 + 10, M = N << 1, mx = 20;
int ch[M][26], fa[M], len[M], ed[M], np = 1, tot = 1;
long long cnt[M];
int pa[M][mx];
vector<int> g[M];
char s[N];
int q;
void extend(int c)
{
int p = np; np = ++tot;
len[np] = len[p] + 1, cnt[np] = 1, ed[len[np] - 1] = np;
while (p && !ch[p][c]) {
ch[p][c] = np;
p = fa[p];
}
if (!p) {
fa[np] = 1;
}
else {
int q = ch[p][c];
if (len[q] == len[p] + 1) {
fa[np] = q;
}
else {
int nq = ++tot;
len[nq] = len[p] + 1;
fa[nq] = fa[q], fa[q] = fa[np] = nq;
while (p && ch[p][c] == q) {
ch[p][c] = nq;
p = fa[p];
}
memcpy(ch[nq], ch[q], sizeof ch[q]);
}
}
}
void dfs(int u, int f)
{
pa[u][0] = f;
for (int i = 1; i <= mx - 1; ++i) {
pa[u][i] = pa[pa[u][i - 1]][i - 1];
}
for (auto son : g[u]) {
dfs(son, u);
cnt[u] += cnt[son]; //预处理pa数组的同时对后缀链接树进行dp
}
}
long long ask(int l, int r)
{
int leng = r - l + 1;
int p = ed[r];
for (int i = mx - 1; i >= 0; --i) {
int ff = pa[p][i];
int mxl = len[ff];
if (mxl >= leng) {//当即将倍增跳的父节点代表子串长度最大值大于等于目标串的长度,则跳
p = ff;
}
}
return cnt[p];
}
signed main()
{
scanf("%s%d", s, &q);
for (int i = 0; s[i]; ++i) {
extend(s[i] - 'a');
}
for (int i = 2; i <= tot; ++i) {
g[fa[i]].emplace_back(i);
}
dfs(1, 0);
while (q--)
{
int l, r; scanf("%d%d", &l, &r);
--l, --r;
printf("%lld\n", ask(l, r));
}
return 0;
}