文章目录
- 前言
- 一.冒泡排序
- 前一个数跟后一个数比较
- 后一个数跟前一个数比较
- 优化
- 复杂度与稳定性
- 二.插入排序
- 初始化条件从第一个元素开始
- 初始化条件从第二个元素开始
- 复杂度与稳定性
- 三.选择排序
- 一趟选出一个最小的
- 一趟选出一个最大的和一个最小的
- 复杂度与稳定性
- 四.堆排序
- 建堆用向下调整
- 建堆用向上调整
- 复杂度与稳定性
- 五.希尔排序
- 初始化条件为0,结束条件为size-gap
- 初始化条件为gap,结束条件为size
- 复杂度与稳定性
- 六.快速排序
- 原始Hore版本
- 挖坑法
- 前后指针法
- 非递归快排
- 前序遍历
- 层序遍历
- 复杂度与稳定性
- 优化
- 三数取中
- 设置随机key
- 七.归并排序
- 递归写法
- 非递归写法
- 一把梭哈
- 分步拷贝
- 稳定性与时间复杂度
- 八.计数排序
- 复杂度
前言
以下排序,实现的都是升序
为了简化操作:这里将打印函数和交换函数以及头文件先给出
#include<stdio.h>
#include<stdbool.h>
void Swap(int* n1, int* n2)
{
int tmp = *n1;
*n1 = *n2;
*n2 = tmp;
}
void Print(int* arr,int size)
{
for (int i = 0; i < size; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
建议:先写一趟的,再写全部的
- 补充知识:排序的稳定性指的是:排序前后相同数据的相对位置变化的情况,如果排序之后没有发生变化化,我们就称这个排序算法是稳定的!
一.冒泡排序
- 思想:通过两两打擂台的方式,强者胜出,每个人都打一次,从而筛选出一个冠军,把冠军排除在外,让剩余的人继续打,再打一次筛选亚军,以此类推得出每一个人的排名。
- 把人换成数字带进去便可理解冒泡的思想
- 交换条件: 后一个数小或者前一个数大
- 我用的是:前一个数大
//动态图使用的数组:
int arr[] = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 };
int size = sizeof(arr) / sizeof(arr[0]);

前一个数跟后一个数比较
- 起点从第一个元素开始,到倒数第二个元素结束
void BubbleSort1_0(int *arr,int size)
{
//总躺数:size - 1,最后一趟只剩下最后一个数就不用比了
for (int i = 0; i < size - 1; i++)
{
//拿前一个数跟后一个数比较的一趟
for (int j = 0; j < size - 1 - i; j++)
{
//如果前一个数大就交换
if (arr[j] > arr[j + 1])
{
Swap(&arr[j], &arr[j + 1]);
}
}
}
}
后一个数跟前一个数比较
- 第一趟的起点从第二个元素开始,终点到最后一个元素
void BubbleSort2_0(int* arr, int size)
{
//总躺数:size - 1,最后一趟只剩下最后一个数就不用比了
for (int i = 0; i < size - 1; i++)
{
//拿后一个数跟前一个数比较的一趟
for (int j = 1; j < size - i; j++)
{
//如果前一个数大就交换
if (arr[j-1] > arr[j])
{
Swap(&arr[j], &arr[j - 1]);
}
}
}
}
优化
- 当比较完一趟时,如果有序不用再比了。
void BubbleSort1_1(int* arr, int size)
{
//总躺数:size - 1,最后一趟只剩下最后一个数就不用比了
for (int i = 0; i < size - 1; i++)
{
//若是有序的就跳出,假设是有序的
bool Is_Order = true;
//拿前一个数跟后一个数比较的一趟
for (int j = 0; j < size - 1 - i; j++)
{
//如果前一个数大就交换,如果是无序的才会进去if
if (arr[j] > arr[j + 1])
{
Swap(&arr[j], &arr[j + 1]);
Is_Order = false;
}
}
if (Is_Order)
{
break;
}
}
}
复杂度与稳定性
- 最坏的情况:排升序数据是降序,排降序时升序——O(N2)
时间复杂度的准确函数表达式:F(N)=1+2+……+N-1=(N-1)*N/2=N2 / 2 - N / 2
- 最好的情况:排升序是升序,排降序时降序——O(N),这是优化之后的冒泡
在接近有序的情况下:数据的准确函数表达式为:F(N)=a*N,a是大于等于1的正整数
- 空间:没有使用额外的空间——O(1)
- 稳定性:因为相同数据前后并不会发生交换,因此冒泡排序算法稳定。
二.插入排序

- 思想:洗牌
- 先从牌头开始洗,遇到大于的就把牌插入它的前面,以此类推。

初始化条件从第一个元素开始
void InsertSort1_0(int* arr, int size)
{
for (int i = 0; i < size-1; i++)//结束条件:倒数第二个数
{
int cur = arr[i + 1];//这里要注意边界问题
int end = i;
while (1)
{
if (end >= 0 && arr[end] > cur)
{
arr[end + 1] = arr[end];
end--;
}
else
{
arr[end + 1] = cur;
break;
}
}
}
}
初始化条件从第二个元素开始
void InsertSort1_1(int* arr, int size)
{
for (int i = 1; i < size; i++)//结束条件为:倒数第一个元素
{
int cur = arr[i];
int end = i - 1;
while (end >= 0)
{
if (cur < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = cur;
}
}
复杂度与稳定性
- 最坏的情况:排升序数据是降序,排降序时升序——O(N2)
函数表达式:F(N)=1+2+3+4+5+……+N=(N+1)*N / 2
- 最好的情况:接近有序——O(N)
函数表达式:F(N)=a*N,a为正整数
与冒泡比较,插入排序较好,原因是在接近有序的情况下,插入相当于只需遍历一次,冒泡至少要遍历两次。
- 没有用额外的空间——O(1)
- 相等的数据并不会发生交换,因此插入排序的稳定性很好
三.选择排序

一趟选出一个最小的
- 选完之后,与最左边交换
- 处理好的数据就不再动了
void SelectSort1_0(int* arr, int size)
{
//总的比较次数
for (int j = 0; j < size; j++)
{
//先选出最小的下标
int min = j ;
for (int i = j+1; i < size; i++)
{
if (arr[min] > arr[i])
{
min = i;
}
}
//与正在处理的最左边的数据进行交换
Swap(&arr[min], &arr[j]);
}
}
一趟选出一个最大的和一个最小的
- 当选完之后,一种特殊情况:
- 最大的下标与交换的最左边下标时,最左边下标是最小值的下标
- 因此:交换之后,要更新最小值的下标为最大值的下标。
void SelectSort1_1(int* arr, int size)
{
int begin = 0;
int end = size - 1;
while (begin < end)
{
int max = begin;
int min = begin;
//选出最大的和最小的
for (int i = begin+1; i <= end; i++)
{
if (arr[max] < arr[i])
{
max = i;
}
if (arr[min] > arr[i])
{
min = i;
}
}
Swap(&arr[max], &arr[end]);
if (end == min)
{
min = max;
}
Swap(&arr[min], &arr[begin]);
//更新处理的数据范围
end--;
begin++;
}
}
复杂度与稳定性
- 最坏的情况与最好的情况相同——O(N2)
第一种:选出最小的时间复杂度的函数表达式F(N)=1+2+3+……N-1=N2 / 2 - N / 2
第二种:选出最大的和最小的时间复杂度表达式F(N)=2+4+6+8+……+N-1=(N-1+2)*(N-1)/2/2=(N2-1)/4
- 没有用额外的空间——O(1)
- 假如对1,1,-1排序,选出最小的-1会对最左边的1进行交换,破坏了1,1的相对顺序,因此选择排序是不稳定的
四.堆排序
- 核心思想:排升序建大根堆,排降序建小根堆
- 注意:下标与边界问题

建堆用向下调整
void AdjustDown(int* arr, int parent, int size)
{
//假设左孩子是比较大的
int child = 2 * parent + 1;
while (child < size)
{
//如果右孩子大就把孩子给右孩子
if (child + 1 < size && arr[child + 1] > arr[child])
{
child++;
}
if (arr[child] > arr[parent])//孩子大就进行交换
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
}
//小于等于就跳出循环
else
{
break;
}
}
}
void HeapSort(int* arr, int size)
{
//升序建大堆
for (int i = ((size - 1) - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, size);
}
int end = size - 1;//最后一个数的下标
while (end)//end为0表明只有一个数据,因此不用再循环
{
Swap(&arr[end], &arr[0]);
end--;
AdjustDown(arr, 0, end + 1);//这里的end+1指的是需要管理的数据个数
}
}
建堆用向上调整
void AdjustUp(int* arr, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (arr[parent] < arr[child])
{
Swap(&arr[parent], &arr[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapSort(int* arr, int size)
{
//升序建大堆
for (int i = 1; i < size; i++)
{
AdjustUp(arr, i);
}
int end = size - 1;//最后一个数的下标
while (end)//end为0表明只有一个数据,因此不用再循环
{
Swap(&arr[end], &arr[0]);
end--;
AdjustDown(arr, 0, end + 1);//这里的end+1指的是需要管理的数据个数
}
}
复杂度与稳定性
- 向下调整建堆的时间复杂度为O(N),向上调整建堆的时间复杂度为O(NlogN),排序的时间复杂度为O(NlogN),综合看堆排序的时间复杂度为O(N*logN)
- 由于是在数组里面建堆的。没有使用额外的空间——O(1)
- 当堆是2,1,1时,2会先与最后的1发生交换,破坏了相同数据的相对位置,因此堆排序是不稳定的
五.希尔排序
- 思想:想象一下你要到很远的地方,拜访朋友,你大概率不会走路过去,假设是坐飞机过去,到飞机场这时离朋友的家不算太远了,但大概率走路需要很远才到,这时又做出租车过去,又离朋友更近一步,到朋友家一段距离我们都会出于礼貌,再步行一段距离到朋友家。
- 代入希尔排序:先坐飞机,再坐出租车,最后走路,这样初速度很大,但在慢慢变小的,整体在趋近有序,这就是希尔排序的思想
- gap其实就是我们换乘的工具——飞机,出租车,走路

初始化条件为0,结束条件为size-gap
void ShellSort(int *arr,int size)
{
int gap = size;
while (gap > 1)
{
gap = gap / 3+1;//加1是为了要处理的gap等于2时的情况
for (int i = 0; i < size-gap ; i++)
{
int cur = arr[i+gap];
//cur指向最后一个元素下标时为:size-gap+gap-1即为size-1
int end = i;
while (end >= 0)
{
if (cur < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = cur;
}
}
}
初始化条件为gap,结束条件为size
void ShellSort(int *arr,int size)
{
int gap = size;
while (gap > 1)
{
gap = gap / 3+1;//加1是为了要处理的gap等于2时的情况
for (int i = gap; i < size ; i++)
{
int cur = arr[i];
int end = i-gap;
while (end >= 0)
{
if (cur < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = cur;
}
}
}
复杂度与稳定性
- 很遗憾由于一些的数学难题尚未被攻破,时间复杂度我们很难进行准确的计算,但是一些局部的数据表明希尔排序的时间复杂度为:O(N1.25)到O(1.65N1.25)范围内,这是Knuth提出的,并且做了大量的实验数据。
- 没有使用额外的空间——O(1)
- 因为希尔排序在排序1,1,-1假如gap为2,这里的1和-1会交换位置,从而破坏了相同数据1,1的相对位置,因此希尔排序是不稳定的。
六.快速排序
原始Hore版本

void QuickSort(int *arr,int left,int right)
{
if(left>=right)
{
return;
}
int key=left;
int begin = left;
int end =right;
while(begin<end)
{
while(begin<end&&arr[end]>=arr[key])
{
end--;
}
while(begin<end&&arr[begin]<=arr[key])
{
begin++;
}
Swap(&arr[begin],&arr[end]);
}
key = end;
Swap(&arr[left],&arr[key]);
//剩余[left,key-1]与[key+1,right]
QuickSort(arr,left,key-1);
QuickSort(arr,key+1,right);
}
- 循环内部和外部都得保证begin小于end
- 左边先走,保证了最后遇到的是比key小的数
- 当遇到和key 相等的数据时,在左边和在右边都无所谓,因此不用管。
- 走完一趟后已经排好一个数的位置了,剩余的区间为[left,key-1]与[key+1,right]
- 走完一趟后还需要更新key值。
- 递归的返回条件:left>=right
挖坑法

- 因为第一个坑位在最左边,所以首先要保存key值
- 右边先走找到小的就放进坑位,左边后走找大的放进坑位
- 坑位在不断更新
- 最后一个坑位:左边等于右边,即为key值的下标
- 最后把坑里放进key值即可
void QuickSort2_0(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int key = arr[left];
int hole = left;
int begin = left;
int end = right;
while (begin < end)
{
while (begin < end && arr[end] >= key)
{
end--;
}
Swap(&arr[end], &arr[hole]);
hole = end;
while (begin < end && arr[begin] <= key)
{
begin++;
}
Swap(&arr[begin], &arr[hole]);
hole = begin;
}
arr[hole] = key;
//剩余[left,hole-1]与[hole+1,right]
QuickSort2_0(arr, left, hole - 1);
QuickSort2_0(arr, hole + 1, right);
}
前后指针法

- cur找比key小的,prev用于交换数据
- cur与prev之间存的是比key大的数,prev以及以前存的是小于等于key的值
- 最后cur走完数组,prev的位置就是坑位
void QuickSort3_0(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int key = left;
int prev = left;
int cur = left+1;
while (cur <= right)//注意等于,这里的right是数组的
{
if (arr[cur] < arr[key])
{
prev++;
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[prev], &arr[key]);
key = prev;
//剩余[left,key - 1]与[key + 1,right]
QuickSort3_0(arr, left, key - 1);
QuickSort3_0(arr, key + 1, right);
}
非递归快排
- 非递归要使用的单趟排序,这里先列出来
- 由于要使用栈和对列的结构,C语言得自己搓(我这里就省了)
- 栈和对列的结构可自行在此文章里复制:栈和对列
int _QuickSort(int* arr, int left, int right)
{
int key = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (arr[cur] < arr[key])
{
prev++;
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[prev], &arr[key]);
key = prev;
return key;
}
前序遍历
void QuickSortNonR1_0(int* arr, int left, int right)
{
Stack s;
StackInit(&s);
StackPush(&s, right);
StackPush(&s, left);
while (!StackEmpty(&s))
{
int begin = StackTop(&s);
StackPop(&s);
int end = StackTop(&s);
StackPop(&s);
int key = _QuickSort(arr, begin, end);
//[begin,key-1]
//[0,1]
//两个元素:key-1>begin
if (key - 1 > begin)
{
StackPush(&s, key - 1);
StackPush(&s, begin);
}
//[key+1,end]
if (key + 1 < end)
{
StackPush(&s, end);
StackPush(&s, key + 1);
}
}
}
层序遍历
void QuickSortNonR1_1(int* arr, int left, int right)
{
Queue q;
QueueInit(&q);
QueuePushBack(&q, left);
QueuePushBack(&q, right);
while (!QueueEmpty(q))
{
int begin = QueueTop(q);
QueuePopFront(&q);
int end = QueueTop(q);
QueuePopFront(&q);
int key = _QuickSort(arr, begin, end);
//[begin,key-1][key+1,end]
if (begin < key - 1)
{
QueuePushBack(&q,begin);
QueuePushBack(&q, key - 1);
}
if (key + 1 < end)
{
QueuePushBack(&q,key + 1);
QueuePushBack(&q, end);
}
}
}
复杂度与稳定性
-
时间复杂度
在理想状况下
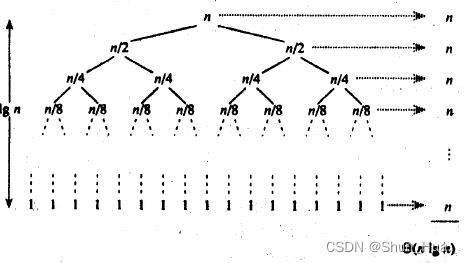
每一层排序N个数据,设分h次把数据分完,则2的h次方就等于N个数据
则:高度为log2N
因此理想状况下时间复杂度为:O(N*log2N)
最坏的情况
当排升序数据是降序时,递归是N*(N-1)(N-2)……1——高度是N
如图:
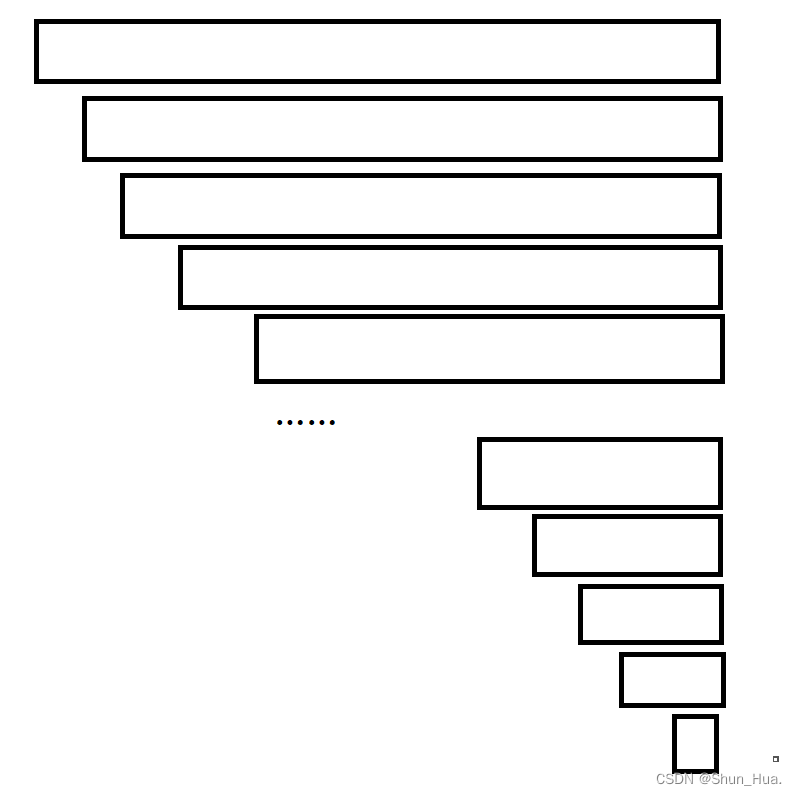
时间复杂度可以估算为O(N2)
这样数据大的话递归层数过多,甚至会导致栈溢出! -
空间复杂度——递归层数为logN到N因此空间复杂度为——O(logN)到O(N)
-
稳定性
在排序1 2 -1 -1时,由于左边的数据会先交换——1 -1 -1 2,破坏了相同数据的相对位置,因此快排不是稳定的。
优化
三数取中
int GetMid(int* arr, int left, int right)
{
int mid = (left + right) / 2;
if (arr[mid] > arr[left])
{
if (arr[right] >= arr[mid])
{
return mid;
}
else//arr[mid]>a[right]
{
if (arr[right] >= arr[left])
{
return right;
}
else
{
return left;
}
}
}
else//arr[left]>=arr[mid]
{
if (arr[mid] >= arr[right])
{
return mid;
}
else//arr[right]>arr[mid]
{
if (arr[right] >= arr[left])
{
return left;
}
else
{
return right;
}
}
}
}
设置随机key
void Randkey(int* arr, int left, int right)
{
srand((unsigned int)time(NULL));
int key = rand() % (right - left) + left;
Swap(&arr[key], &arr[left]);
}
- 以上两种将最坏的情况的可能降到最低,但是如果大量的数据相同呢?
- 时间复杂度毫无疑问还是O(N2),有什么方法解决吗?
- 答案是有的——三路划分
七.归并排序

递归写法
- 将数据被拆分成有序的情况——一个的一个数据
- 再将一个数据和另一数据进行排序。
- 然后再用一组中含有连个数据排序与另一组中两个数据进行排序
- 依次类推,直到整个数据有序
- 排序需要用到另一个数组,排序完然后拷贝回去。
- 注意:拷贝回去的起点需要注意。
//这是由于要开辟数据所以写了两个函数
void _MergeSort(int* arr, int* tmp, int left, int right)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
_MergeSort(arr, tmp, left, mid);
_MergeSort(arr, tmp, mid + 1, right);
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] <= arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
memcpy(arr + left, tmp + left, sizeof(int) * (right - left + 1));
//切记arr跟arr+left指向的位置可不一样!
}
void MergeSort(int* arr, int size)
{
int* tmp = (int*)malloc(sizeof(int) * size);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
_MergeSort(arr, tmp, 0, size-1);
}
非递归写法
- 从递归的最底层进行排序,也就是gap等于1
- 不断分组进行排序——相当于倒着的层序遍历
- 每一层遍历之后gap乘等2,直到大于原数组的大小为止
- 其次还要考虑边界的处理
一把梭哈
void MerageSortNonR1_0(int* arr, int size)
{
int* tmp = (int*)malloc(sizeof(int) * size);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
int gap = 1;
while (gap < size)
{
for (int i = 0; i < size; i += 2*gap)
{
//归并的两个区间
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
//修正越界的部分
//首先begin1是不可能越界的
//end1越界
//修正end1
//因为梭哈要全拷贝
//修正end2与begin2满足begin2>=end2
//begin2越界
//修正end2与begin2满足begin2>=end2
//end2越界
//修正end2
if (end1 >= size)
{
end1 = size - 1;
begin2 = size;
end2 = size - 1;
}
else if (begin1 >= size)
{
begin2 = size;
end2 = size - 1;
}
else if (end2 >= size)
{
end2 = size - 1;
}
//排序
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] <= arr[begin2])
{
tmp[j++] = arr[begin1++];
}
else
{
tmp[j++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = arr[begin2++];
}
}
//一下子梭哈
memcpy(arr, tmp, sizeof(int) * size);
//调整gap
gap *= 2;
}
}
分步拷贝
void MerageSortNonR1_1(int* arr, int size)
{
int* tmp = (int*)malloc(sizeof(int) * size);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
int gap = 1;
while (gap < size)
{
for (int i = 0; i < size; i += 2 * gap)
{
//归并的两个区间
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
//修正越界的部分
//首先begin1是不可能越界的
//end1越界与begin2越界
//直接跳出循环即可
//end2越界
//修正end2
if (end1 >= size||begin2>=size)
{
break;
}
else if (end2 >= size)
{
end2 = size - 1;
}
//排序
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] <= arr[begin2])
{
tmp[j++] = arr[begin1++];
}
else
{
tmp[j++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = arr[begin2++];
}
//注意这里end2不能减去begin1+1因为这里的begin1在循环之后已经成为begin1l
//真正的左区间是i
memcpy(arr+i, tmp+i, sizeof(int) * (end2-i+1));
}
//调整gap
gap *= 2;
}
}
稳定性与时间复杂度
- 时间复杂度
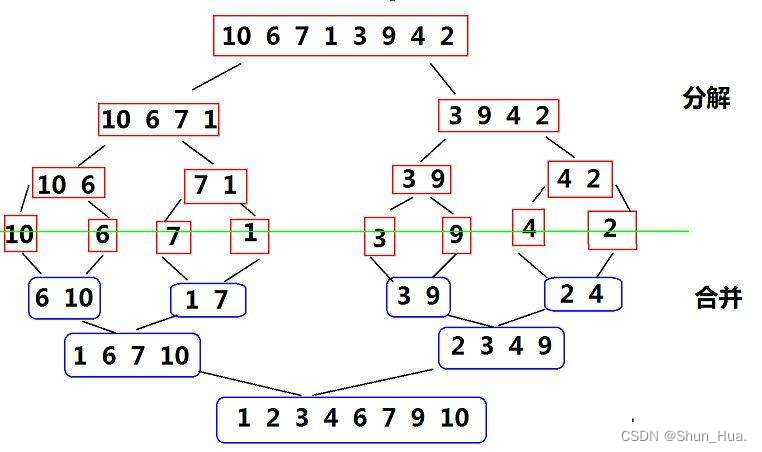
可以类比快排的理想状态,这里每一层都要排序,排序的次数等于层数。
设节点有N个。层数为h
则:2h = N,
h = log2N
因此时间复杂度为层数乘以每次排序的次数——O(N*logN)
-
空间复杂度
递归的空间消耗为——O(logN)
额外开辟的空间为——O(N)
因此:空间复杂度为O(N) -
稳定性
在排序 1 12 和 1 2两组有序数组 时,1 2 和 1 2,如果相等则先放左边的,后放右边的,这样相对顺序就不会发生变化,因此归并排序是稳定的。
八.计数排序

void CountSort(int* arr, int size)
{
//第一步:找最大最小确定数的范围
int max = arr[0];
int min = arr[0];
//可不敢初始化为0,因为0不一定在数组内部
for (int i = 0; i < size; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
int range = max - min + 1;
//假如0到9为最大和最小,则[0,9]一共有9-0+1=10个数
int* Count = (int*)calloc(range, sizeof(int) * range);
if (Count == NULL)
{
perror("calloc fail");
exit(-1);
}
//下标与数的关系为
//F =x-min,F是下标,min是最小值,x是数
//这是可以存负数的!
//当存的最小值是-9时,下标为-9-(-9)= 0,最小值的下标为0
for (int i = 0; i < size; i++)
{
Count[arr[i] - min]++;
}
//将记过的数再拷贝回原数组
for (int i = 0,j = 0; i < range; i++)
{
while (Count[i]--)
{
arr[j++] = i + min;
}
}
}
复杂度
- 时间复杂度
在最大与最小值相差较小时,且数据比较集中(计数排序有奇效)时,我们可认为时间复杂度为O(N)
在最大值与最小值相差较大时,我们认为时间复杂度为O(N+range),range为最大值与最小值的数据范围。
- 空间复杂度
计数的数组的大小是额外开辟的空间,因此空间复杂度为O(range),range意思同上
- 稳定性
由于计数排序不是对原数组进行直接排序,所以稳定性我们不加讨论。