来源：力扣（LeetCode）

描述：

给定一个长度为 n 的链表 head

对于列表中的每个节点，查找下一个 更大节点 的值。也就是说，对于每个节点，找到它旁边的第一个节点的值，这个节点的值 严格大于 它的值。

返回一个整数数组 answer ，其中 answer[i] 是第 i 个节点( 从1开始 )的下一个更大的节点的值。如果第 i 个节点没有下一个更大的节点，设置 answer[i] = 0 。

示例 1：

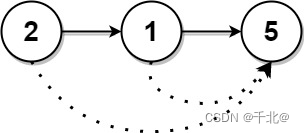
输入：head = [2,1,5]
输出：[5,5,0]

示例 2：

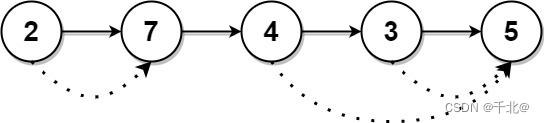
输入：head = [2,7,4,3,5]
输出：[7,0,5,5,0]

提示：

• 链表中节点数为 n
• 1 <= n <= 10⁴
• 1 <= Node.val <= 10⁹

方法：单调栈

思路与算法

找出「下一个更大的元素」是经典的可以用单调栈解决的问题。

我们对链表进行一次遍历，同时维护一个内部值单调递减（不是严格单调递减，可以相等）的栈。栈中的元素对应着还没有找到下一个更大的元素的那些元素，它们在栈中的顺序与它们在链表中出现的顺序一致。这也解释了为什么栈中的值是单调递减的：如果有两个元素不满足单调递减的限制，那么后一个元素大于前一个元素，与「还没有找到下一个更大的元素」相矛盾。

当我们遍历到链表中的值为 val 的节点时，只要它大于栈顶元素的值，我们就可以不断取出栈顶的节点，即栈顶节点的下一个更大的元素就是 val。在这之后，我们再将 val 放入栈顶，为其在后续的遍历中找到它的下一个更大的元素，同时也保证了栈的单调性。

细节

当我们取出栈顶的元素时，我们是不知道它在链表中的位置的。因此在单调栈中，我们需要额外存储一个表示位置的变量。

代码：

class Solution {
public:
    vector<int> nextLargerNodes(ListNode* head) {
        vector<int> ans;
        stack<pair<int, int>> s;

        ListNode* cur = head;
        int idx = -1;
        while (cur) {
            ++idx;
            ans.push_back(0);
            while (!s.empty() && s.top().first < cur->val) {
                ans[s.top().second] = cur->val;
                s.pop();
            }
            s.emplace(cur->val, idx);
            cur = cur->next;
        }

        return ans;
    }
};

执行用时：76 ms, 在所有 C++ 提交中击败了60.09%的用户
内存消耗：41.6 MB, 在所有 C++ 提交中击败了42.92%的用户
复杂度分析
时间复杂度：O(n)，其中 n 是链表的长度。对链表进行遍历需要 O(n) 的时间，链表中的每个元素恰好入栈一次，最多出栈一次，这一部分的时间也为 O(n)。
空间复杂度：O(n)，其中 n 是链表的长度。即为单调栈需要的空间。
author：LeetCode-Solution