一、定点数及其定标
在定点DSP芯片中，采用的是定点数据数值运算，其操作数一般采用整形数来表示。一个整形数的最大表示范围由DSP芯片给定字长决定。字长越长，表示的范围越大，精度越高。
举例16位字长
每个16数位用1个符号位表示正负，0表示正，1表示负，其余15位表示数值大小。因此
二进制数 0010000000000011b 即十进制数8195
二进制数1111111111111100b 即十进制数-4
对于DSP而言，参与数值运算的数是16位整形数，而许多情况下，数学运算过程中的数不一定都是整数，那么，DSP芯片是如何处理小数的呢？是这样的，DSP芯片本身不可以，是不是芯片不能处理各种小数呢？当然不是，这关键就是由程序员来确定一个数的小数点处于16位中哪一位，给这个数定标。
二进制转换为十进制的计算方法如下：1个具有n+1位整数m位小数的二进制数表示为：
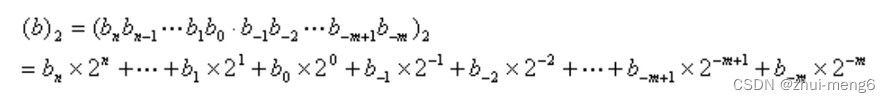比如
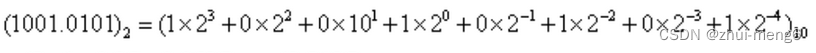
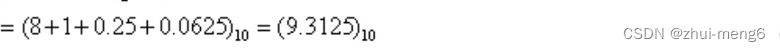以上数据的下标2、10分别表示2进制、10进制。
通过设定小数点在16位数不同位置，而表示不同大小和不同精度的小数，数的定标有Q表示法和S表示法2种。
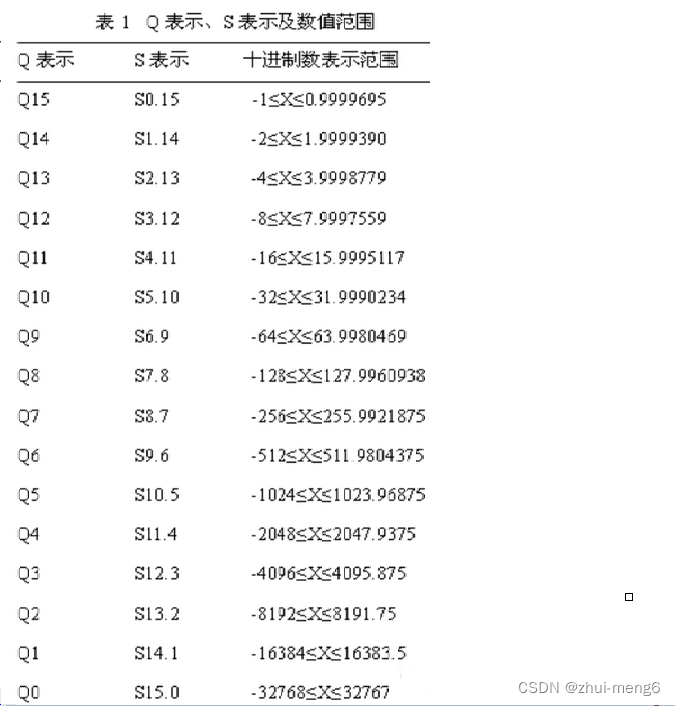若小数点设定的位置不同，它所表示的数也就不同。例如：
16 进制数 2000H＝8192，用 Q0 表示
16 进制数 2000H＝0.25，用 Q15 表示
其中 Q0 表示小数的位数为 0，整数 15 位，符号 1 位；Q15 表示小数的位数是 15，整数 0 位，符号 1 位。
但对于DSP而言，不管小数设置在什么位置，处理方法完全相同，都看成16位整数，真正的数据是什么由程序员设定的Q来计算。因此，对定点数而言，数值范围与精度是反比关系，一个变量想要表示大的数值范围，必须牺牲精度为代价。
例如，Q0 的数值范围是-32768 到+32767，其精度为 1，而 Q15 的数值范围为-1 到 0.9999695，精度为 1/32768 = 0.00003051。

二、浮点数(x)与定点数(xq)的转换关系
浮点数(x)转换为定点数(xq)：xq=(int)x* 2Q
定点数(xq)转换为浮点数(x)：x=(float)xq2-Q
例如，浮点数x=0.5，定标Q=15，则定点数xq=L0.532768J=16384，式中LJ表示下取整。反之，一个用Q=15表示的定点数16384，其浮点数为163幼*2-15=16384/32768=0.5。浮点数转换为定点数时，为了降低截尾误差，在取整前可以先加上0.5。

三、浮点数
是属于有理数中某特定子集的数的数字表示法。定点数由于要对数定标，编程时难度较大，数据的精度也会受到一定的影响。若用浮点数，则简单方便很多。
浮点数分为两种表示形式：一种是一般格式（也是百度常见的） 另一种是IEEE754标准格式。
1、一般表示格式：阶码就是指数；阶符就是指数的符号；数符是指尾数的符号，它们各占多少位取决于表示范围，表示精度等方面的权衡。比如32位长的浮点数，阶符和阶符各用1位，阶码可以用7位，尾数23位；阶符和阶码也可以结合起来，用一个8位来表达，一般格式中将数符放在中间部分，这与定点表示格式不一致，而且在计算机处理时也不够方便，因此实际中一般采用IEEE754来表示格式
2、IEEE754标准格式
N=M×R^E
比如：12.345=1.2345×10^1
其中，M(Mantissa)被称为浮点数的 尾数 ，R(Radix)被称为阶码的 基数 ，E(Exponent)被称为阶的 阶码 。计算机中一般规定R为2、8或16，是一个确定的常数，不需要在浮点数中明确表示出来。以上为字长32位。

2.1、尾数M的值，通常由小数形式表示，决定浮点数的精度，23位，但实际是24位，有一个位是“不可见”的，其值固定为1，这也就是说IEEE 754 标准所定义的浮点数，其有效数字是介于 1 与 2 之间的小数，因此尾数 m=1.f。
2.2、阶码E通常用定点整数表示，决定浮点数的表示范围，8位。
2.3、符号位：1位，0表示正数，1表示负数。

3、浮点数据转换16进制数据的原理
以32位字长即4个字节的数据位准：4*8=32位31位为符号，30~23的八个字节为阶码，尾数部分则是剩余的小数部分（由后23位决定）
3.1将数据（10进制，浮点型）转换成2进制；
3.2小数点向左移动n位，指导最后1个为1停止，得到左移的位数，计算阶码，127+（左移位数）；
3.3尾数（22~0位置总计23个bit位）为小数部分的二进制编码，剩余未填满的位数用0补齐；
3.4再将所有得到的2进制编码，转换成16进制的数据。
4、举例：将10进制4.25表示成机器内4个字节的2进制形式
4.1第1步：将4.25表示成2进制数:(4.25)(十进制)=(100.01)(二进制)
4.2第2步小数点向左移2位，变成1.0001x2^2，阶码E(Exponent)=2+127=129;
4.3第3步Mantissa=1.0001-1.0=0001（规格化后，小数点前总是整数1，所有人都知道前面是1不是0，所以省略不写了，即尾数部分不包括整数部分；
4.4转换成16进制数81010000
举例4.5、以小数点为界，拆分；
4.6、整数部分转换：整数转二进制我想大家应该都熟悉，使用：除2取余法 即可。而这里的0.875整数部分为0，无需操作；
4.7、小数部分转换：小数部分的转换不同于整数部分，采用的是 “乘2取整法”。
如下图所示：
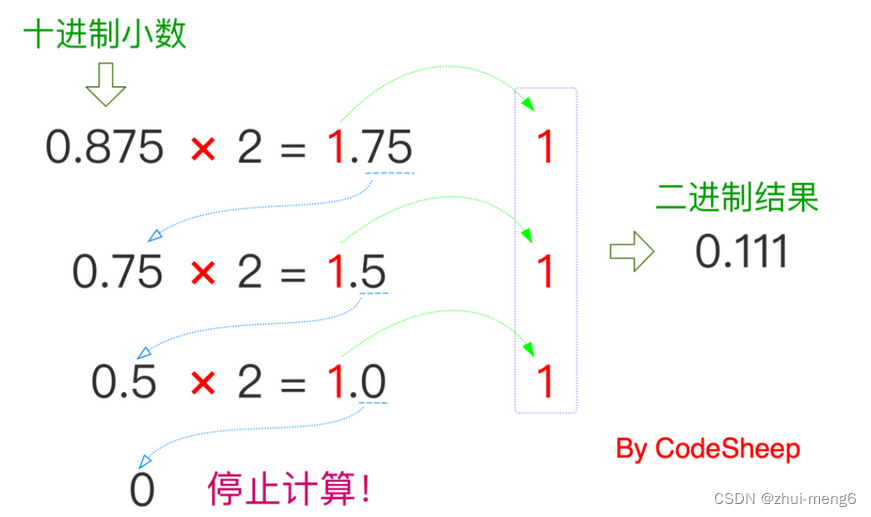合并结果：整数部分 + 小数部分，最终得到二进制结果为0.111。
所以该结果按照尾数 + 阶码的计算机计数方式，可以表示为：
阶码（E）：若以float为例，应为127 + （-1） = 126，因此，二进制表示为：01111110
尾数部分（M）：若以float为例，应为23位，因此尾部补齐后为11000000000000000000000
因此，最终的结果为（以32位精度float表示）：00111111011000000000000000000000
举例sigmaStudio中float转int

5、浮点类型转换十六进制代码实现方法
5.1、用地址用指针
void flout2int(float src, int *dst)
{
*dst = ((int)(&src));
}
5.2、用memcpy
#include “stdio.h”
#include “string.h”
void flout2int(float src, int *dst)
{
memcpy(&dst,&src,sizeof(float));
}

参考来源：
https://blog.csdn.net/qq_36915078/article/details/106019023
https://blog.csdn.net/qq_43537721/article/details/107757766
https://blog.csdn.net/qq_36915078/article/details/106019023
https://blog.csdn.net/ADI_OP/article/details/129021375?spm=1001.2014.3001.5502