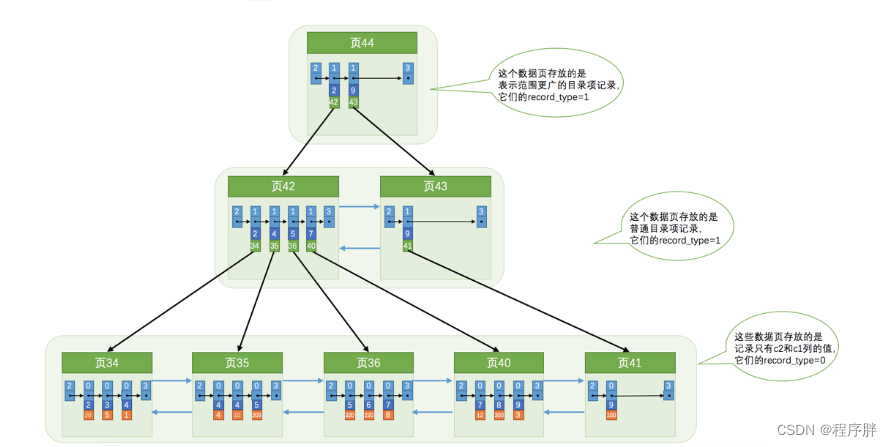
一个左节点u << 1和右节点u << 1 | 1 的证明

区间修改部分
1.批量等值修改
前提条件
是要区间修改,区间查询,且修改操作修改的值是相同的
情景
一般是要对一个数组执行k次操作,每次改变其中一个区间内所有元素的值,然后询问一个区间内所有元素的最值或总和,
题解代码
void Pushdown(int k){ //更新子树的lazy值,这里是RMQ的函数,要实现区间和等则需要修改函数内容
if(lazy[k]){ //如果有lazy标记
lazy[k<<1] += lazy[k]; //更新左子树的lazy值
lazy[k<<1|1] += lazy[k]; //更新右子树的lazy值
t[k<<1] += lazy[k]; //左子树的最值加上lazy值
t[k<<1|1] += lazy[k]; //右子树的最值加上lazy值
lazy[k] = 0; //lazy值归0
}
}
注意懒标记中储存区间修改的值与长度的乘积,大概率开long long
struct node {
int l, r;
ll val;
ll lazy;
}t[N << 2];
void pushdown(node& op, ll lazy) {
op.val += lazy * (op.r - op.l + 1);
op.lazy += lazy;
}
void pushdown(int x) {
if (!t[x].lazy) return;
pushdown(t[x << 1], t[x].lazy), pushdown(t[x << 1 | 1], t[x].lazy);
t[x].lazy = 0;
}
void build(int l, int r, int x = 1\没有值传入时,默认初始化为1) {
t[x] = { l, r, w[l], 0 };
if (l == r) return;
int mid = l + r >> 1;
build(l, mid, x << 1), build(mid + 1, r, x << 1 | 1);
pushup(x);
}
void modify(int l, int r, int c, int x = 1) {
if (l <= tr[x].l && r >= tr[x].r) { pushdown(tr[x], c); return; }\通过打标记的方法来赋值
pushdown(x);
操作时遇到了懒标记就处理下(懒的思想,顺路就搞下,不顺路就拖着不干)
int mid = tr[x].l + tr[x].r >> 1;
if (l <= mid) modify(l, r, c, x << 1);\modify的递归也变成了和线段树单点修改query里的递归形式,有交集就递归。
if (r > mid) modify(l, r, c, x << 1 | 1);
pushup(x);
}
ll ask(int l, int r, int x = 1) {
if (l <= t[x].l && r >= tr[x].r) return tr[x].val;
pushdown(x);
//query的唯一变化就是加上了一个pushdown();
int mid = tr[x].l + tr[x].r >> 1;
ll res = 0;
if (l <= mid) res += ask(l, r, x << 1);
if (r > mid) res += ask(l, r, x << 1 | 1);
return res;
}
int main()
{
int n, m; cin >> n >> m;
rep(i, n) scanf("%d", &w[i]);
build(1, n);
while (m--) {
char op[2]; int l, r; scanf("%s %d %d", op, &l, &r);
if (*op == 'Q') printf("%lld\n", ask(l, r));
else {
int c; scanf("%d", &c);
modify(l, r, c);
}
}
return 0;
}
自己写的acwing式代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
struct node{
int l,r;
ll sum;
ll lazy;
}tr[N<<2];
int w[N];
void pushdown(node &x,ll lazy){
x.sum += lazy*(x.r - x.l + 1);
x.lazy += lazy;
}
void pushdown(int u){
if(!tr[u].lazy) return;
pushdown(tr[u<<1],tr[u].lazy),pushdown(tr[u<<1|1],tr[u].lazy);
tr[u].lazy = 0;
}
void pushup(int u){
tr[u].sum = tr[u<<1].sum + tr[u<<1|1].sum;
}
void build(int u,int l,int r){
tr[u].l = l,tr[u].r = r,tr[u].sum =w[r];
if(l == r) return;
int mid = l + r >> 1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
ll query(int u,int l,int r){
if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
ll res = 0;
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if(l <= mid) res += query(u<<1,l,r);
if(r > mid) res += query(u<<1|1,l,r);
return res;
}
void modify(int u,int l,int r,int v){
if(tr[u].l >= l && tr[u].r <= r){
pushdown(tr[u],v);
return;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(u<<1,l,r,v);
if(r > mid) modify(u<<1|1,l,r,v);
pushup(u);
}
int main(){
int n,m;
cin >> n >> m;
for(int i =1;i <= n;i++) scanf("%d",&w[i]);
build(1,1,n);
while(m--){
char op[2];
int l,r;
scanf("%s%d%d",op,&l,&r);
if(*op == 'Q') printf("%lld\n",query(1,l,r));
else{
int c;
scanf("%d",&c);
modify(1,l,r,c);
}
}
return 0;
}
注意:
线段树的初始化在build里完成,多组数据集时不需要再额外初始化。
2.批量自适应修改
前提条件
是区间修改,区间查询,且修改操作的修改的值是根据具体节点储存的值而变化的,比如开根,幂,替换,乘除;
情景
对一个序列里的元素执行k次自适应操作,每次操作一个区间,然后询问区间内所有元素的值。
也有询问某个区间内所有值经过某种处理后的值。(此种问法是询问时用一个变量储存找到的值,经过处理后返回
例题1单种操作
Can you answer these queries?
22ACM集训队-树状数组与线段树基础 - Virtual Judge (vjudge.net)
主要就是把modify的递归条件改成了和传统query操作相同的有交集
复杂度比较高,可能需要一些剪枝,某条件下操作了等于白操作之类的。
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
struct node{
int l,r;
ll sum;
}tr[N<<2];
ll w[N];
void pushup(int u){
tr[u].sum = tr[u<<1].sum + tr[u<<1|1].sum;
}
void build(int u,int l,int r){
tr[u] = {l,r,w[r]};
// cout << w[r] << endl;
if(l == r) return;
int mid = l + r >> 1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
ll query(int u,int l,int r){
if(tr[u].l >= l && tr[u].r <= r) {
return tr[u].sum;
}
// cout << tr[u].sum;
ll res =0 ;
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) res += query(u<<1,l,r);
if(r > mid) res += query(u<<1|1,l,r);
return res;
}
void modify(int u,int l,int r){
if(tr[u].l == tr[u].r) tr[u].sum = sqrt(tr[u].sum);
else{
if(tr[u].l >= l && tr[u].r <= r && tr[u].sum == tr[u].r - tr[u].l + 1) return;
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(u<<1,l,r);
if(r > mid) modify(u<<1|1,l,r);
pushup(u);
}
}
int main()
{
int T = 1;
int n, m;
while (cin >> n) {
for(int i = 1;i <= n;i++) scanf("%lld", &w[i]);
build(1,1, n);
printf("Case #%d:\n", T++);
scanf("%d", &m);
while (m--) {
int op, l, r; scanf("%d %d %d", &op, &l, &r);
if (l > r) swap(l, r);
// cout << l << " " << r << endl;
if (op) printf("%lld\n", query(1,l, r));
else modify(1,l, r);
}
printf("\n");
}
return 0;
}
例题2多种操作
Transformation HDU - 4578
22ACM集训队-树状数组与线段树基础 - Virtual Judge (vjudge.net)
题解代码
Transformation HDU - 4578 (线段树,审题很重要)_Soar-的博客-CSDN博客
#include<bits/stdc++.h>
using namespace std;
#define lson i<<1,l,m
#define rson i<<1|1, m+1,r
const int mod = 10007;
const int maxn=1e5+10;
int x[maxn<<2],flag[maxn<<2];
x是tr,flag是lazy
void pushup(int i,int l,int r)
{
if(!flag[i<<1] || !flag[i<<1|1])左右子节点无值
flag[i] = 0;
else if(x[i<<1] != x[i<<1|1])左右子节点有值且不等
flag[i] = 0;
else flag[i]=1,x[i]=x[i<<1];左右子节点值相等
所以这是一个记录懒标记的函数,如果左右子节点的值相同,就上传。
通过用父节点的节点的值来代表子节点的值接受处理,降低复杂度
}
void pushdown(int i,int l,int r)
{
if(flag[i])
{
flag[i<<1] = flag[i<<1|1] =1;
x[i<<1] = x[i<<1|1] = x[i];
flag[i]=0;
}
这是一个下传懒标记并处理懒标记的函数,如果有懒标记,说明这个节点是代表子节点接受处理的,所以直接将值下传到子节点,然后清除懒标记
}
void update(int ql,int qr,int p,int v,int i,int l,int r)
{
妙:直接传入op,也就是p,根据p的值进行不同操作,减少了很多赘余的代码。
我写时想的是写3个modify,也就是update,根据op不同,调用不同的modify,麻烦得很。
if(ql<=l && qr>=r && flag[i])
这里是有懒标记,且节点区间全都在需要处理的区间内,直接处理当前节点,然后pushdown,就可以实现区间处理
{
if(p==1)
x[i] = (x[i]+v)%mod;
else if(p==2)
x[i] = (x[i]*v)%mod;
else x[i] = v;
修改当前节点值的话是不需要pushup的,因为pushup的操作是根据子节点的值来决定是否赋予当前节点一个懒标记,只修改当前节点值,代表当前节点已经是叶子节点,或者左右节点值相同,所以就算pushup了,懒标记还是会保持原有状态
return;
}
pushdown(i,l,r);
可能没有懒标记,会需要逐个单点修改,所以用两个if的原始query递归形式
int m = (l+r)>>1;
if(ql<=m) update(ql,qr,p,v,lson);
if(qr>m) update(ql,qr,p,v,rson);
进行子节点单点值修改操作后都需要pushup,来更新懒标记状态
pushup(i,l,r);
}
int query(int ql,int qr,int num,int i,int l,int r)
l,r是当前节点的l,r
{
if(flag[i] && ql<=l && qr>=r)
{
int ans=1;
for(int j=0;j<num;j++)ans=(ans*x[i])%mod;//pow操作,每次pow取余,如果是10007的三次方就有可能爆int了,所以用循环来每次操作后取余
ans=(ans*(r-l+1))%mod;
return ans;
}
pushdown(i,l,r);
int m = (l+r)>>1;
int ans=0;
if(ql<=m)ans+=query(ql,qr,num,lson);
if(qr>m)ans+=query(ql,qr,num,rson);
return ans%mod;
}
int main()
{
int n,m;
while(cin>>n>>m,n||m)
{
memset(flag,1,sizeof flag);
memset(x,0,sizeof x);
int p,x,y,v;
while(m--)
{
scanf("%d%d%d%d",&p,&x,&y,&v);
if(p>=1 && p<=3)update(x,y,p,v,1,1,n);
else printf("%d\n",query(x,y,v,1,1,n));
}
}
}
经过模仿后得到的acwing版代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10,mod = 10007;
struct node{
int l,r;
int sum;
int lazy;
}tr[N<<2];
void pushup(int u){
if(!tr[u<<1].lazy || !tr[u<<1|1].lazy) tr[u].lazy = 0;
有一个子节点懒标记是0(当前节点的子节点的两个子节点的值不相等)则当前节点懒标记就变成0,由此可以推断出,懒标记的含义是表示当前节点的子树里所有节点的值 ,都相等,可以直接用当前节点的值来进行操作。
else if(tr[u<<1].sum != tr[u<<1|1].sum) tr[u].lazy = 0;
else tr[u].lazy = 1,tr[u].sum = tr[u<<1].sum;
}
void pushdown(int u){
if(tr[u].lazy){
tr[u<<1].lazy = tr[u<<1|1].lazy = 1;
tr[u<<1].sum = tr[u<<1|1].sum = tr[u].sum;
tr[u].lazy = 0;
}
}
void build(int u,int l,int r){
tr[u] = {l,r,0,1};
if(l == r) return;
int mid = l + r >> 1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}
void modify(int u,int l,int r,int op,int v){
if(tr[u].l >= l && tr[u].r <= r && tr[u].lazy){
if(op == 1) tr[u].sum = (tr[u].sum + v) % mod;
else if(op == 2) tr[u].sum = (tr[u].sum * v)%mod;
else {
tr[u].sum = v;
}
return;
}
pushdown(u);
有懒标记要先处理,然后再运算。
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(u<<1,l,r,op,v);
if(r > mid) modify(u<<1|1,l,r,op,v);
pushup(u);
}
int query(int u,int l,int r,int v){
if(tr[u].l >= l && tr[u].r <= r && tr[u].lazy){
int res = 1;
for(int i = 0;i < v;i++) res = (res * tr[u].sum) % mod;
res = res * (tr[u].r - tr[u].l + 1) % mod;
return res;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
int res = 0;
if(l <= mid) res = (res + query(u<<1,l,r,v) ) %mod;
if(r > mid) res = (res + query(u<<1|1,l,r,v)) % mod;
return res % mod;
}
int main(){
int n,m;
while(cin >> n >> m,n||m){
// for(int i=0;i <= N << 2;i++) tr[i]= {0,0,0,0};
build(1,1,n);
int op,l,r,v;
while(m--){
scanf("%d%d%d%d",&op,&l,&r,&v);
// cout << op << " " << l << " " << r << " " << v << endl;
if(op >=1 && op <= 3){
modify(1,l,r,op,v);
}
else {
printf("%d\n",query(1,l,r,v));
}
}
}
return 0;
}
注意
注意点就是非数组模拟节点的代码要用build初始化,然后懒标记初始化为1,因为代表的含义是两个子节点值是否相等
其他套路:
涉及到一个多组输入的套路
前提条件是没有明确组数,结束关键词的多组数据集输入
取反while(~scanf(“%d”,&n)
和while(scanf(“%d”,&n) != EOF)
还有while(cin >> n)三种形式