来源：投稿作者：摩卡
编辑：学姐

数据集简介

实验使用了两个数据集，一个是经典的鸢尾花数据集(iris)另一个是树叶数据集(leaf)

鸢尾花数据集(iris)：

鸢尾花数据集发布于1988年7月1日，该数据集共有150条数据，分为3个类别，为setosa、versicolor、virginica 。

每个类别有50条数据，每条数据有4个特征，分别是sepal_length(范围在4.3-7.9)、sepal_width(范围在2.0-4.4)、petal_length(范围在1.0-6.9)、petal_width(范围在0.1-2.5)。

该数据集没有缺失值，但类别标签是字符串类型，需要进行重新编码(编码时从0开始)

树叶数据集(leaf)：

树叶数据集发布于2014年2月24日，该数据集共有340条数据，有30个类别(有的是在同一类别下但是有学名有不同)，每条数据有15个特征，没有缺失值，类别标签是数字编码无需进行转换。该数据集还提供RGB格式，可以用于计算机视觉任务。

实验工具介绍

硬件：本实验所使用的CPU型号为inter@i5-10210U 1.6GHz-4.2GHz

软件：所使用的软件为Anaconda + Pycharm

框架：所使用的框架为pytorch、使用机器学习库sklearn、pandas、绘图工具matplotlib

实验步骤简介

模型简介

选取了KNN、SVM、K-means、MLP这几个模型进行实验。

K近邻法(k-nearest neighbor, k-NN)

KNN是一个基本的分类方法，由Cover和Hart在1968年提出。

K近邻算法简单直观：

给定一个训练集T={(x1, y1), (x2, y2), (x3, y3), …… ,(xn, yn)}，对于新输入的实例xn+1，在训练集中找到与该实例最相近的k个实例，这k个实例的多数属于某个类，就把该输入实例分到这个类。k-近邻算法可以分为两个部分，一部分是根据训练集构造kd树进行超平面的划分，一部分是根据新输入的实例在kd树中进行搜索来确定新输入实例的类别。

当超平面构造完成，k值选取完毕之后，新实例的标签也就确定了。在进行距离测量时可以选择L1、L2范数，确定新实例所属类别时可以使用多数表决的方法。

支持向量机(support vector machines, SVM)

支持向量机(support vectoe machines)由Cortes和Vapnik提出，最初只是线性支持向量机，适用于可线性分类的数据。后来Boser、Guyon、Vapink又引入了核(kernel)的技巧，提出了非线性支持向量机。

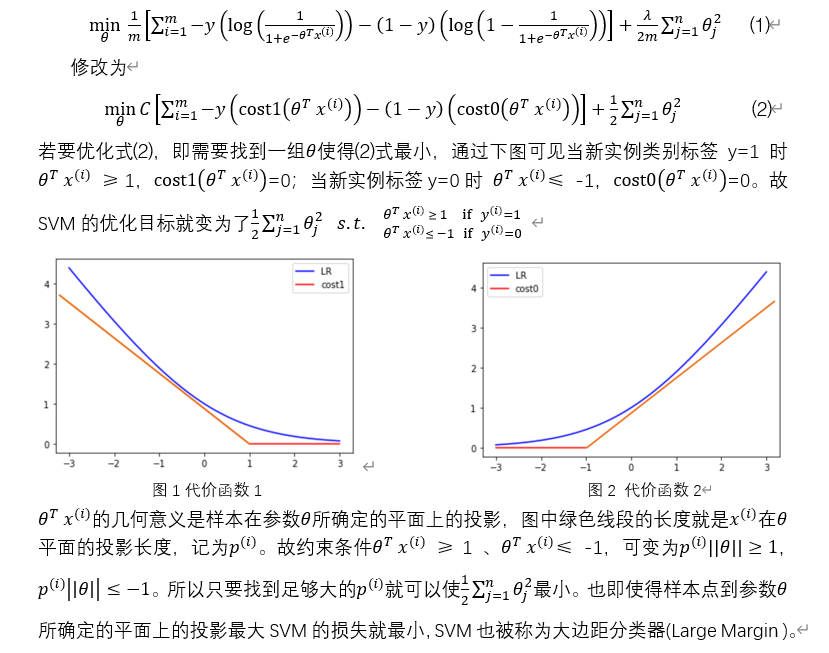
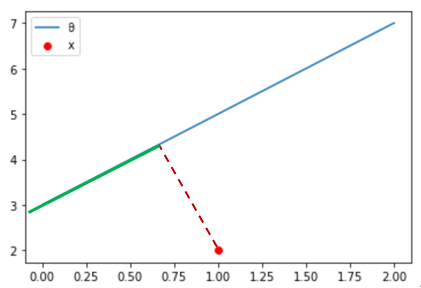
图3 样本点到平面距离

非线性支持向量机(non- linear support vectoe machines)

顾名思义该向量机的决策边界(decision boundary)可以是非线性的。非线性支持向量机在线性向量机的基础上修改了，将修改为。

是一个特征向量，由每个样本与标记点(landmarks)的相似程度构成。

如图中红色的点为标记点(landmarks)，绿色点为当前特征点x，蓝色点为其他特征点x_others。是由x与各个标记点的相似程度构成，当使用高斯核时相似程度的度量函数为

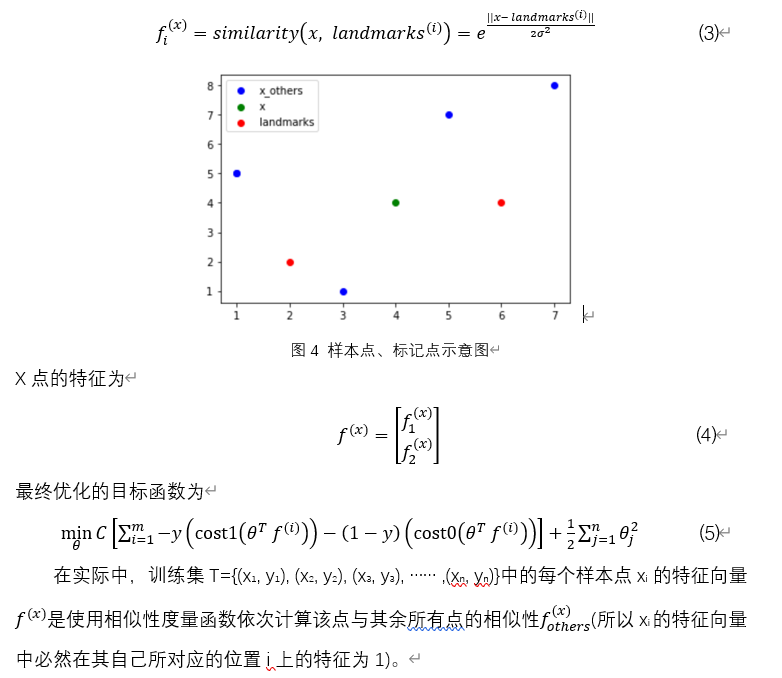
K均值聚类(k-means)

聚类算法针对给定的样本，依据它们特征的相似度或者距离，将其归并到若干“类”或“簇”的分析问题。聚类属于无监督学习，只根据样本的相似度或距离将其进行归类。K-means聚类算法属于中心聚类方法，通过迭代，将样本分摊到k个类中，使得样本与其所属的中心最近。

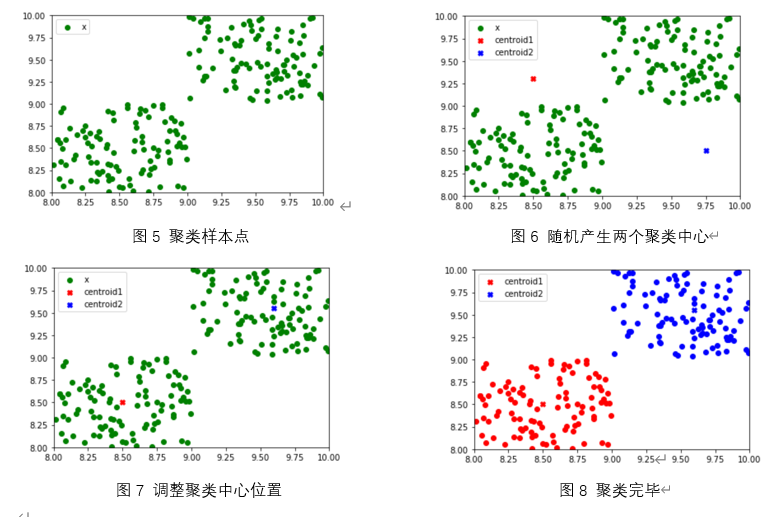
k-means聚类算法分过程为，先随机产生k个聚类中心(centroid)，在训练集中按照样本点距离各中心的距离着色(着色过程也就是分类过程)再根据各类别点计算出均值，作为新聚类中心，如此循环直到聚类结束。

根据上述算法描述可知，K-means聚类的优化对象是各个样本点到聚类中心的距离，

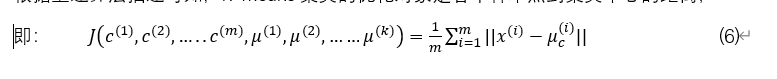
其中为每个样本点被分配到的类，为k个聚类中心，为每个样本点被分配到的聚类中心。

多层感知机(multilayer perceptron，MLP)

多层感知机也叫做深度前馈网络(deep feedforward network)、前馈神经网络(feedforward neural network)。神经网络中最基本的单元是神经元(neuron)模型，每个神经元与其他神经元相连接，神经元收到来自n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数(activation function)处理以产生神经元的输出。

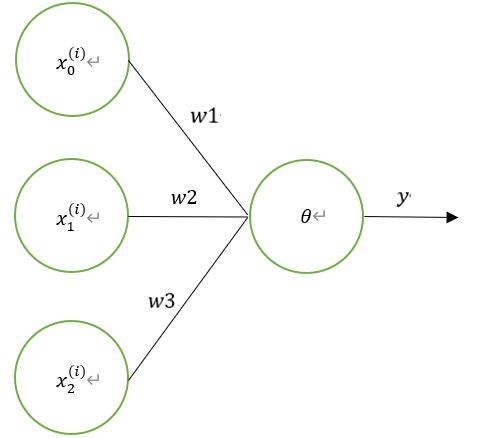
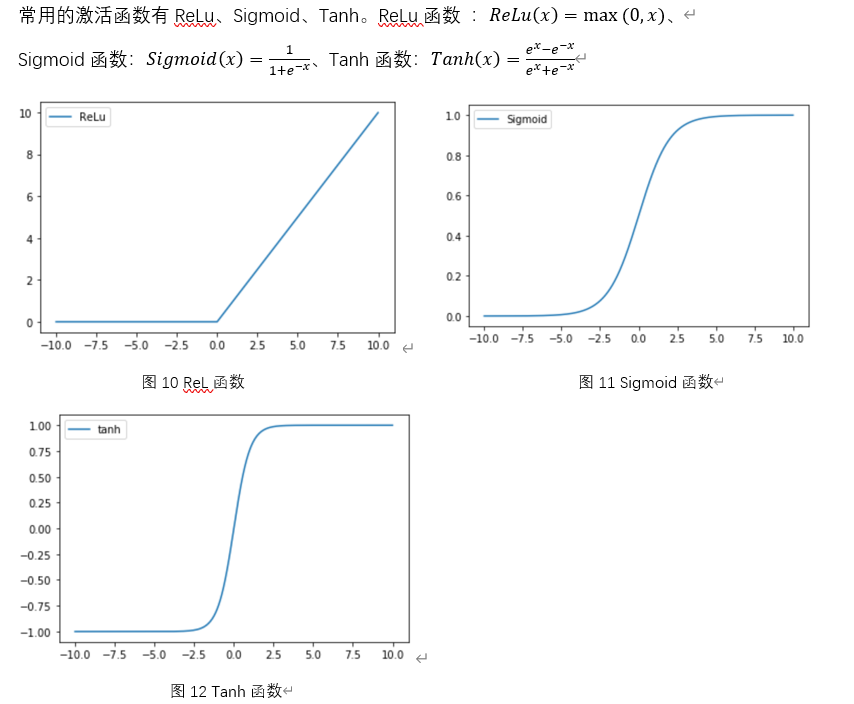
假设有如下图所示结构的网络,该网络从左至右分别为input层、hidden1层、hidden2层、output层。

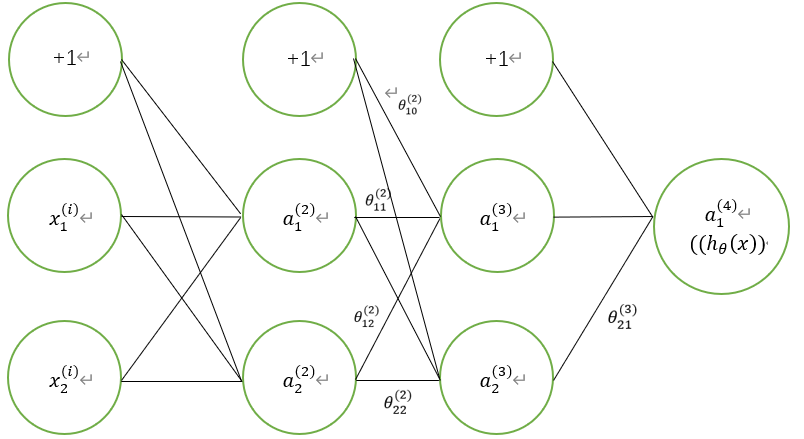
图13 神经网络

约定表示第j层上第i个神经元的激活项，表示第k层的第i个激活项的第j个输入，为激活函数。根据上述前向传播方法可知、、、、为：

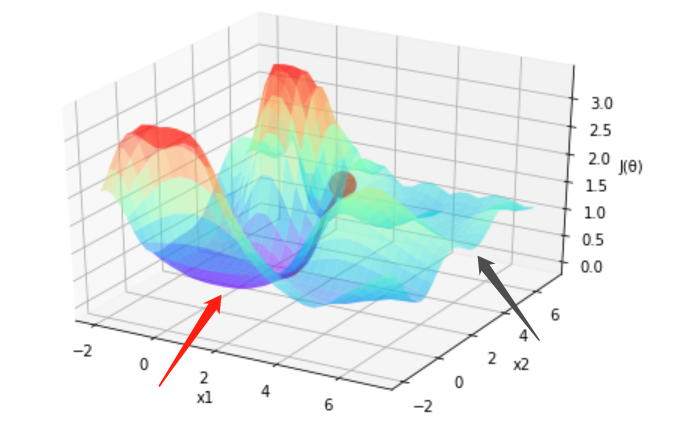
图14 梯度下降局部最优、全局最优

鸢尾花数据集处理

2.1数据预处理

鸢尾花数据集：

使用seaborn库绘制数据集的图像进行分析，根据类别进行分类。得到一下图片。根据下面图像的观察，以花萼长度(sepal_length)与花萼宽度(sepal_width)进行分类时没有很好的将数据分开，所以进行数据清洗的时候将这两个类别清洗掉，以此来提高效率。

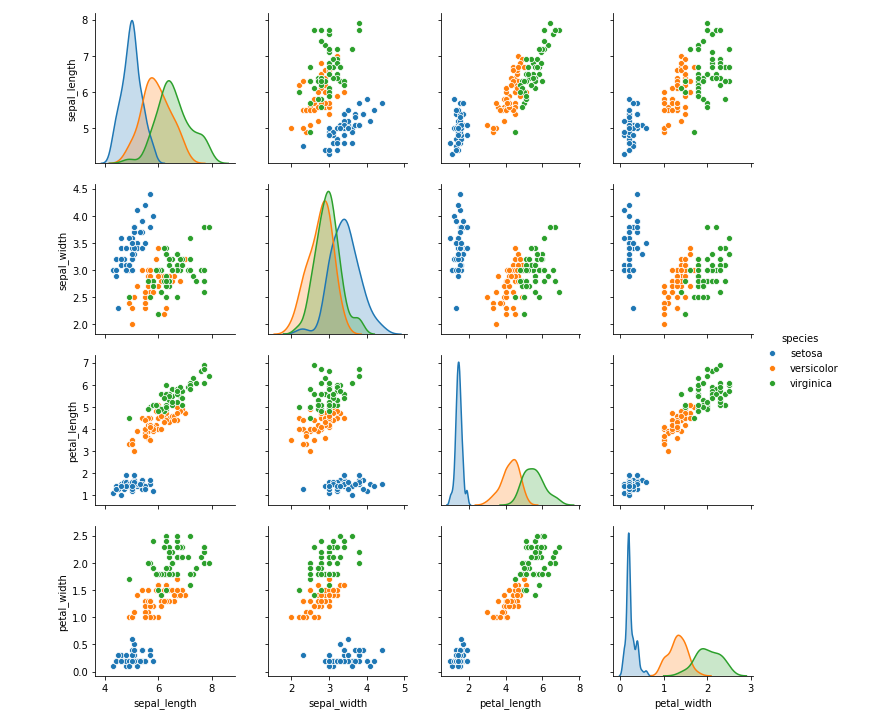
图15 鸢尾花特征可视化1

进行数据清洗完毕后，进行可视化，得到如下结果。

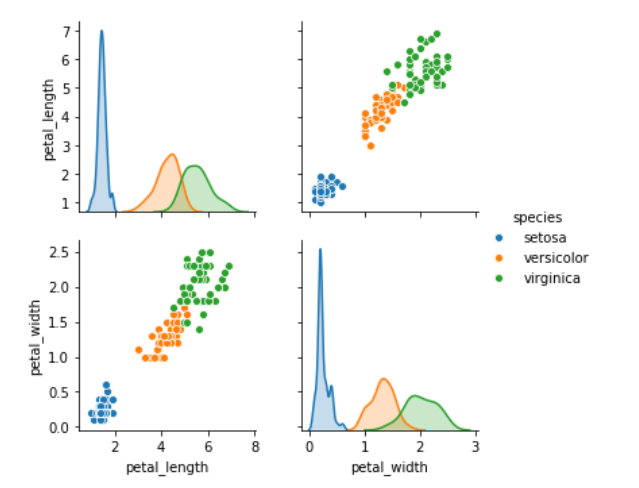
图16 鸢尾花特征可视化2

因为鸢尾花数据集的标签类别项是字符串类型，需要进行编码，使用LabelEncoder()将其编码为0(setosa)、1(versicolor)、2(virginica)。

使用StandardScaler()进行标准化(使用StandardScaler()进行标准化的数学原理为将数据按其属性减去其均值，然后除以其方差。最后得到的结果是，对每个属性/每列来说所有数据都聚集在0附近，方差值为1)。

2.2划分数据集

将数据集划分为训练集(train_dataset)和测试集(test_dataset)两部分，训练集120条数据，测试集有30条数据。

树叶数据集处理

3.1数据预处理

树叶(leaf)数据集共有14个特征和一个类别属性，计算属性与类别的相关系数，并进行热图的绘制。由下图可知，与类别成正相关的属性由高到底排序为B、M、I、K、C、J、L、N、D、A、E，也可以发现属性H、G、F与属性成负相关。

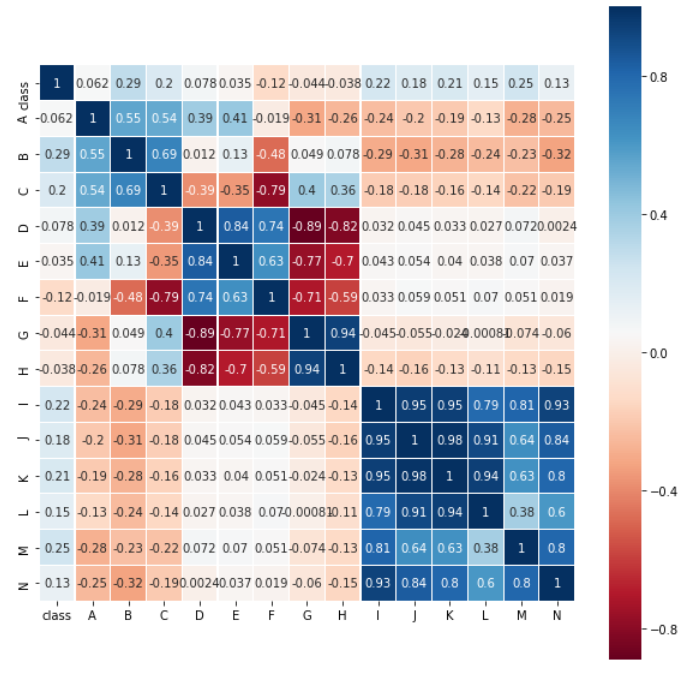
图17 树叶属性热图1

进行数据清洗，除去成负相关的属性H、G、F，得到的热图如下。

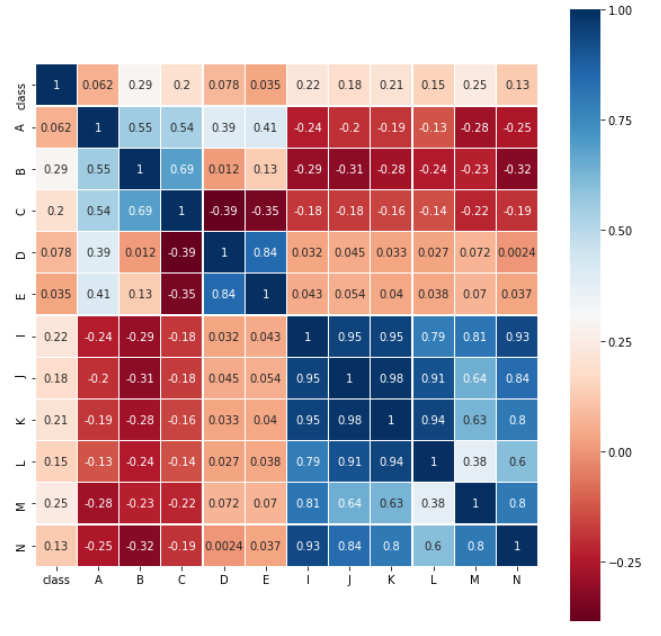
图18 树叶属性热图2

对树叶的类别进行编码使用LabelEncoder() 类别编号从0-29。使用StandardScaler()进行标准化。

3.2划分数据据

将数据集划分为训练集(train_dataset)和测试集(test_dataset)两部分，训练集有210条数据，测试集有130条数据。

鸢尾花数据集分类结果展示

4.1 KNN

使用KNN模型进行分类，测量邻居间距离使用minkowski距离，邻居个数k=5。预测准确率为97%。

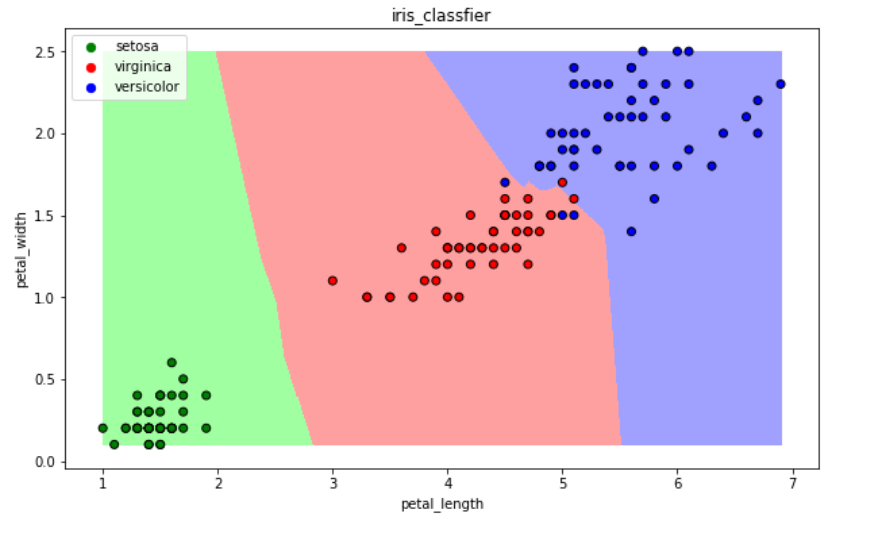
图19 KNN分类边界

图20 KNN评价指标

4.2 SVM

使用SVM进行分类，使用的核函数为高斯核(Gaussian kernel )，超参数C=1.0。预测准确率为97%。

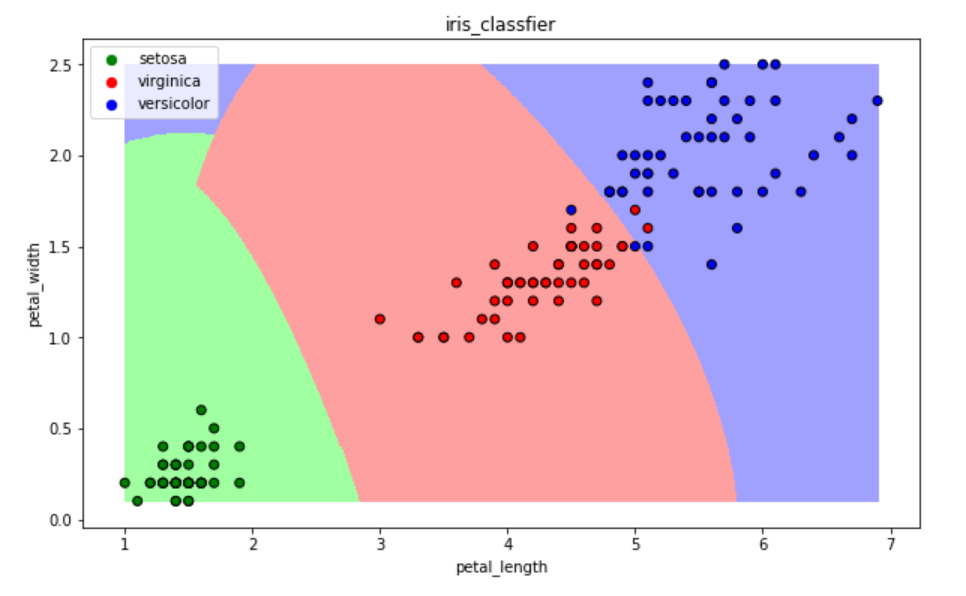
图21 SVM分类边界

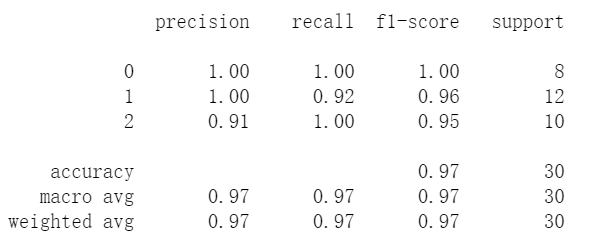
图22 SVM评价指标

4.3 K-means

使用K-means进行分类，簇的个数n_clusters=3，最大迭代次数max_iter=100。预测准确率为97%

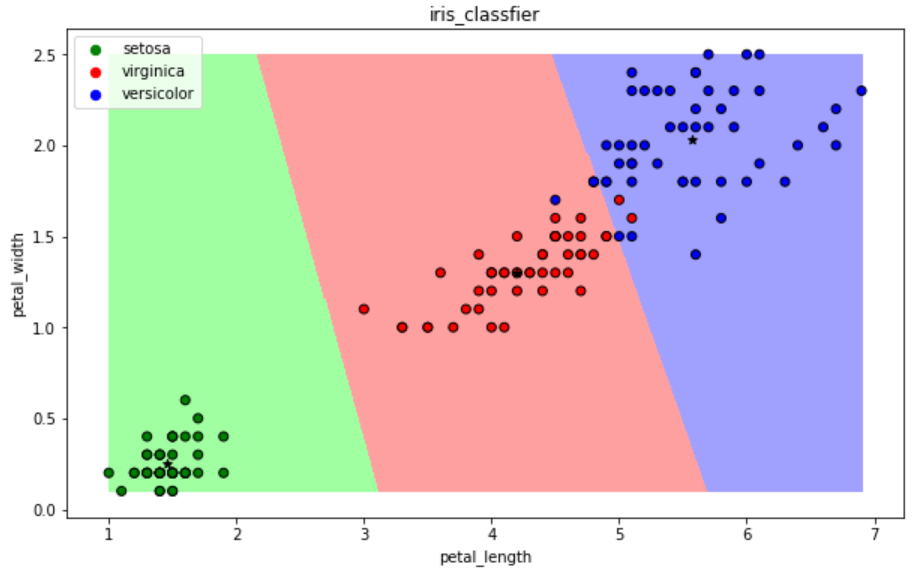
图23 K-means分类边界

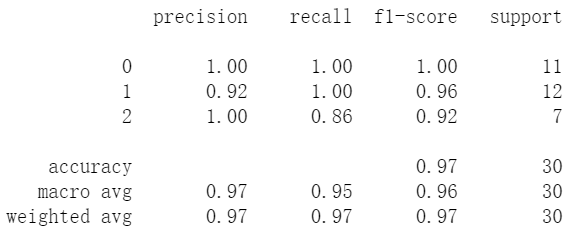
图24 K-means评价指标

4.4 MLP

使用MLP进行分类，构造全连接神经网络，该网络有1个输入层，1个输出层，3个隐藏层。输入层有2个神经元(在数据预处理前input神经元为4个)，隐藏层神经元个数为16个，输出层神经元个数为3个(因为有3个类别，所以输出神经元个数为3)。

隐藏层激活函数为ReLu函数，使用交叉熵损失函数，优化方法使用梯度下降法(SGD)，学习率lr=0.01，momentum=0.9，最大周期max_epoch=50。训练准确率最高为100%，预测准确率最高为97%。

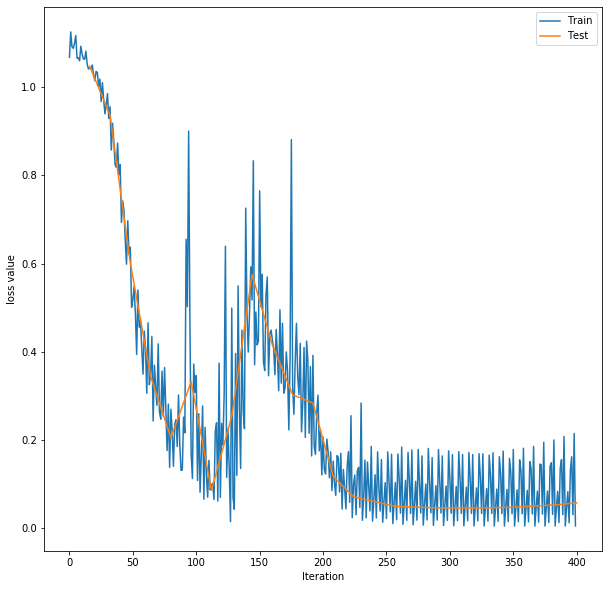
图25 MLP训练、测试损失曲线

图26 MLP评价指标

树叶数据集分类结果

5.1 KNN

使用KNN模型进行分类，由于树叶数据集相比于鸢尾花数据集更复杂，参数的选择也更困难，所以使用网格化搜索最优参数。测量邻居间距离使p=1曼哈顿距离，邻居个数k=4，权重weight=“distance”(权重和距离成反比)，预测准确率为65%。

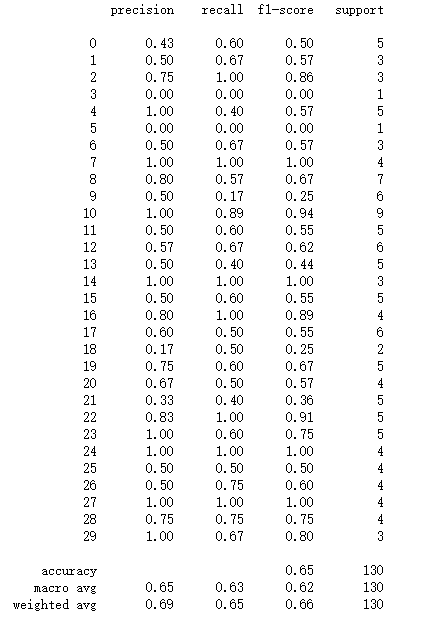
图27 KNN评价指标

5.2 SVM

使用SVM进行分类，同样使用网格化搜索最优参数。使用的核函数为线性核(Linear kernel )，超参数C=1.0、gamma=0.0001。预测准确率为77%。

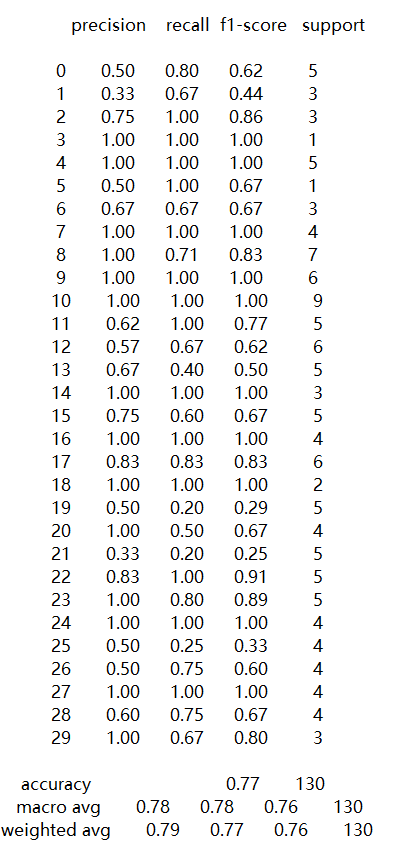
图28 SVM评价指标

5.3 MLP

使用MLP进行分类，构造全连接神经网络，该网络有1个输入层，1个输出层，3个隐藏层。

输入层有14个神经元(在数据预处理后虽然变成11个但是效果不好)，隐藏层神经元个数为23个，输出层神经元个数为30个(因为有30个类别，所以输出神经元个数为30)。

隐藏层激活函数为ReLu函数，还在每层上添加了随即失活，失活率p=0.1，使用交叉熵损失函数，优化方法使用梯度下降法(SGD)，学习率lr=0.01，momentum=0.9，最大周期max_epoch=2500。训练准确率最高为93.3%，预测准确率最高为82.3%。

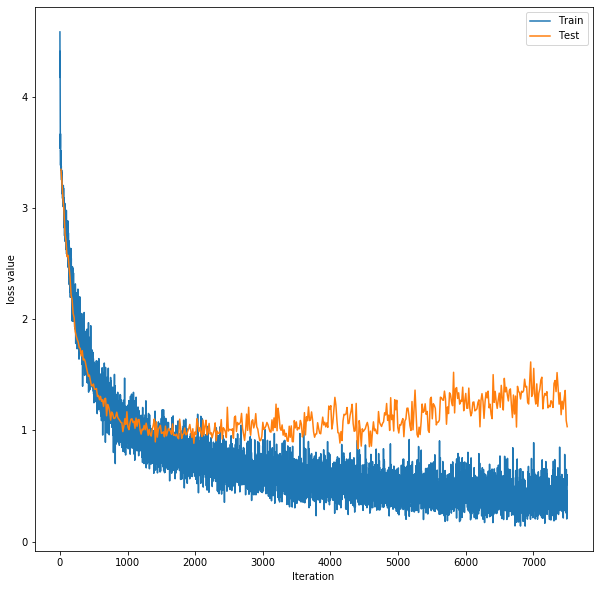
图29 MLP训练、测试损失曲线

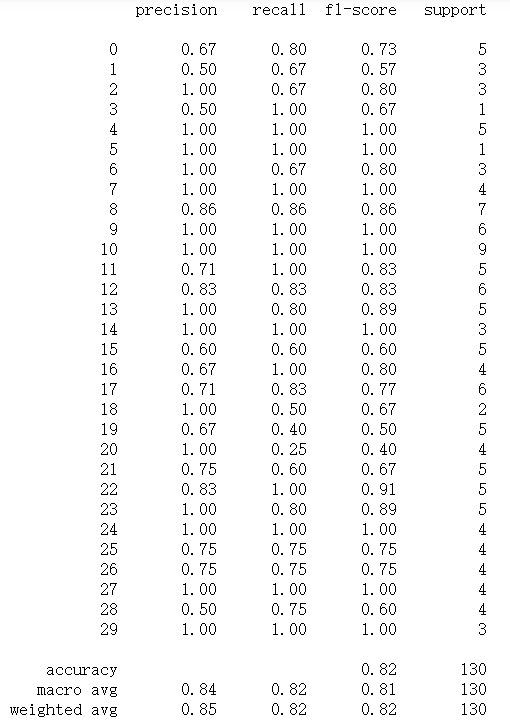
图30 MLP评价指标

实验结果比较

6.1鸢尾花数据集

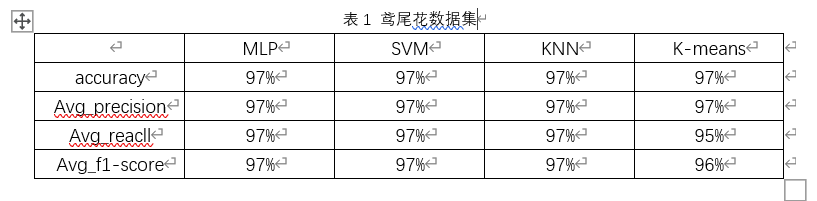
由下图可以看出，MLP、K-means、SVM、KNN四种方法准确率（acc）均为97%。MLP、K-means、SVM、KNN四种方法的平均精度(Avg_precision)均为97%。

MLP、K-means、SVM、KNN四种方法的平均召回率(Avg_recall)：SVM、KNN、MLP皆为97%， K-means为95%。

MLP、K-means、SVM、KNN四种方法的平均召回率(Avg_f1-score) ：SVM、KNN、MLP皆为97%， K-means为96%。

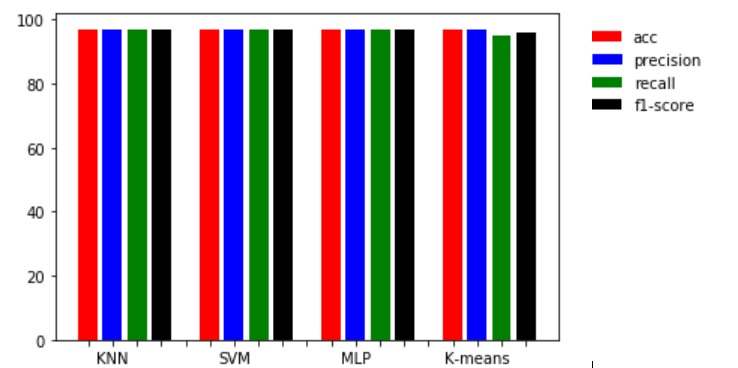
图31 指标比较1

6.2树叶数据集

由下图可以看出，MLP准确率最高为82%，SVM其次为77%，最后是KNN为65%。MLP平均准确率(Avg_precision)率最高为85%，SVM其次为79%，最后是KNN为69%。

MLP平均准确率(Avg_recall)率最高为82%，SVM其次为77%，最后是KNN为65%。MLP平均准确率(Avg_f1-score)率最高为82%，SVM其次为76%，最后是KNN为66%。

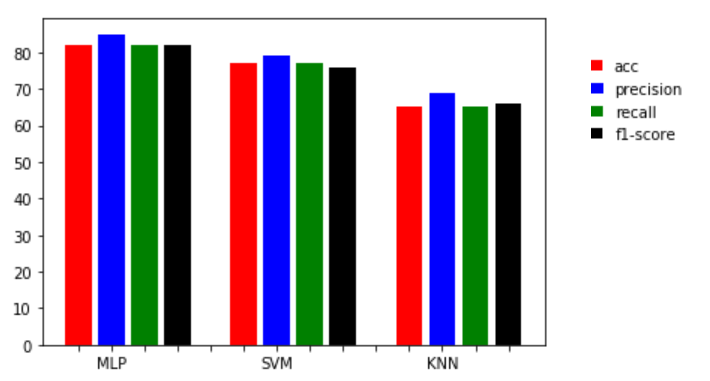
图32 指标比较2

实验结果分析

7.1鸢尾花数据集

通过上面4个模型的accuracy、Avg_precision、Avg_reacll、Avg_f1-score 4个指标的对比可以发现，4个模型对鸢尾花数据集的各项指标都很高。在特征工程部分，将鸢尾花的4个属性进行清洗，只保留了2个重要的属性，使得噪声减少，提高了识别准确率等各项指标。

表1 鸢尾花数据集

7.2树叶数据集

通过上面3个模型的accuracy、Avg_precision、Avg_reacll、Avg_f1-score 4个指标的对比，可以发现，相比于鸢尾花数据集，模型的各项指标都有大幅度的下降。这是由于树叶数据集比鸢尾花数据集更加复杂：类别多(30类)、特征多(14个)。并且在MLP、SVM、KNN三个模型中，MLP表现最好，识别率为82%，其余三项指标也都在82%左右。

表2 树叶数据集