1、数据来源:世界知识产权组织发布的《2021年全球创新指数报告》
2、时间跨度:2013-2020
3、区域范围:全球
4、指标说明:
全球创新指数(Global Innovation Index,GII)是世界知识产权组织、康奈尔大学、欧洲工商管理学院于2007年共同创立的年度排名,衡量全球120多个经济体在创新能力的表现,是全球政策制定者、企业管理执行者等人士的主要基准工具。
全球创新指数是一个详细的量化工具,有助于全球决策者更好地理解如何激励创新活动,以此推动经济增长和人类发展。全球创新指数根据80项指标对126个经济体进行排名,这些指标包括知识产权申请率、移动应用开发、教育支出、科技出版物等。该指数提交给欧洲委员会联合研究中心,进行独立统计审计。
全球创新指数(GII)提供了有关全球127个国家和经济体的创新绩效详细指标。该指数是由康奈尔大学,欧洲工商管理学院和世界知识产权组织(WIPO)合作得出的结果。GII获得了国际认可,既是衡量创新能力的主要参考,也是决策者的“操作工具”。它反映出了在全球经济越来越以知识为基础的背景下,创新驱动的经济发展与社会增长之间的联系。
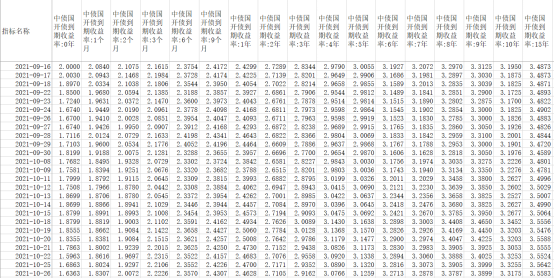
部分数据如下:

相关文献:
[1]崔维军, 陈亚兰. 中国创新型国家建设进程监测与分析——基于全球创新指数的研究[J]. 科技进步与对策, 2013, 30(20):6.
[2]高锡荣, 罗琳, 张红超. 从全球创新指数看制约我国创新能力的关键因素[J]. 科技管理研究, 2017(1):6.
[3]漆苏, 刘立春. 基于全球创新指数的中国创新能力现状及影响因素分析[J]. 科技进步与对策, 2018, 35(18):10.
[4]周频, 甘泗群, 黄跃. 创新型国家建设中的政府作为——基于WIPO《全球创新指数2016》的视野[J]. 中国软科学, 2016, 000(0z1):254-262.
download链接:GII全球创新指数2013-2020-数据集文档类资源-CSDN下载