引言

在计算QUBO解的过程中，通常需要利用不同的优化算法来计算其结果。

在本文中，我们将带领大家利用python基于模拟退火计算QUBO表达式，并且给出了演示的示例。话不多说，我们开始吧。

模拟退火算法

模拟退火是一种启发式算法，用于解决优化问题。

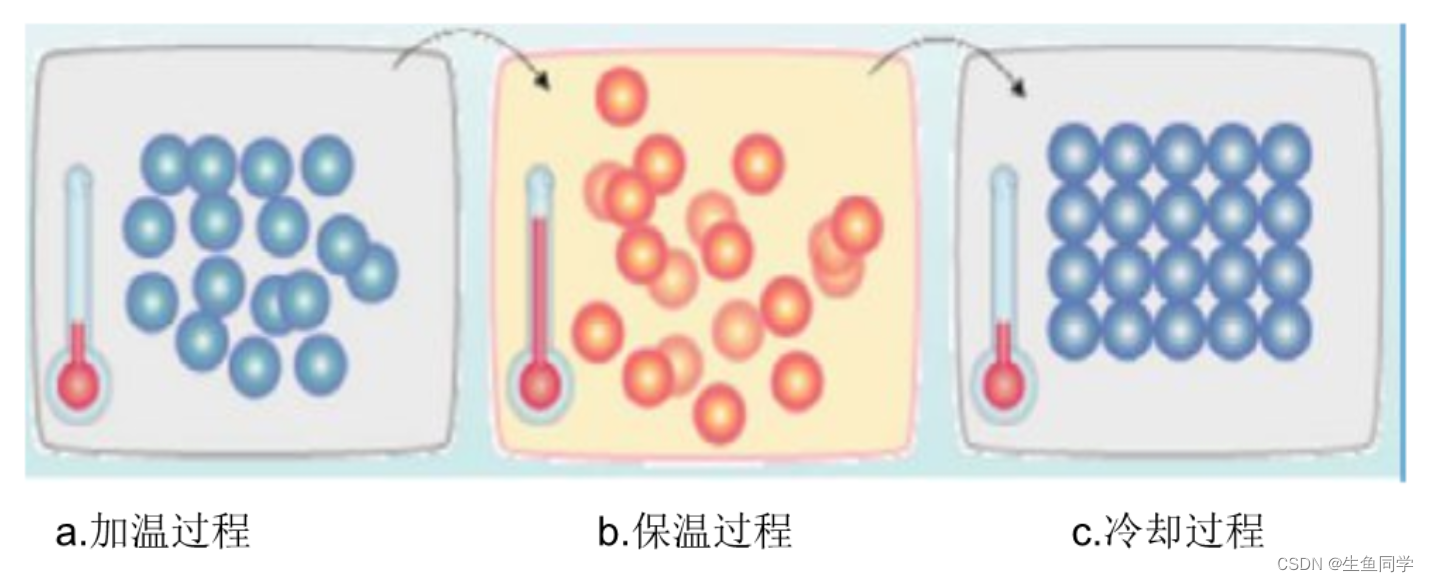
它基于冶金学中的退火过程，在这个过程中，金属被加热并缓慢冷却以获得所需的结构。

模拟退火的理论过程

该算法从一个初始解决方案开始，然后对其进行随机修改，以寻找更好的解决方案。解决方案的质量由一个目标函数来衡量，该算法接受变化，即使它们会导致更差的解决方案，但其概率会随着时间的推移而降低。这使得该算法能够避免陷入局部最优状态，并探索更大的解决方案空间。

在这里插入图片描述

模拟退火在优化中的应用

模拟退火在优化问题中有很多的应用，主要有以下几种：

参数优化：在机器学习中，模拟退火可以通过在参数空间中搜索，找到全局最优解。
组合优化：模拟退火可以通过在可行解空间中随机搜索，以找到最优解。
线性规划：线性规划问题和组合优化类似，也是指在约束条件下最大化或最小化线性目标函数。模拟退火可以在变量空间中搜索，以找到最优规划。
图形匹配：模拟退火可以通过在图形空间中搜索，在两个图形中找到最大的匹配。

基于python的模拟退火编码流程

定义目标函数

在这个函数中，我们需要对目标函数进行定义，在本文中我们假设目标函数如下：

(1 - x)**2 + 100 * (y - x**2)**2

则定义的目标函数为：

#  Rosenbrock 函数
def rosenbrock(x, y):
    return (1 - x)**2 + 100 * (y - x**2)**2

初始化状态

在这里，我们需要对模型的进行一些初始化，代码如下：

# 随机设置初始化状态
current_state = (random.uniform(-5, 5), random.uniform(-5, 5))
# 初始能量，把初始化状态带入目标函数
current_energy = obj_func(*current_state)

另外，我们还需要记录最优解以及能量值：

best_state = current_state
best_energy = current_energy

迭代寻找最优

在这一步中，我们主要分为以下几个部分来进行计算：

根据我们设定的温度以及步长进行降温
随机生成新的状态
计算能量差
判断是否得到的结果更优
如果结果更优则接受新的解，否则以一定的概率接受
更新最优解

循环进行1-6直到达到了迭代次数，下面为代码：

for i in range(num_iter):
        # 根据我们设定的温度以及步长进行降温
        temperature = init_temp * math.exp(-alpha * i)

        # 随机生成新的状态
        new_state = (random.uniform(-5, 5), random.uniform(-5, 5))
        new_energy = obj_func(*new_state)

        # 判断是否得到的结果更优，如果结果更优则接受新的解，否则以某概率接受
        delta_energy = new_energy - current_energy
        if delta_energy < 0:
            current_state = new_state
            current_energy = new_energy
        else:
            acceptance_prob = math.exp(-delta_energy / temperature)
            if random.random() < acceptance_prob:
                current_state = new_state
                current_energy = new_energy

        # 更新最优解
        if current_energy < best_energy:
            best_state = current_state
            best_energy = current_energy

完整代码

import math
import random

def rosenbrock(x, y):
    return (1 - x)**2 + 100 * (y - x**2)**2

def simulated_annealing(obj_func, init_temp, alpha, num_iter):
	# obj_func：目标函数
	# init_temp：目标函数
	# alpha：设顶参数
	# num_iter：迭代次数
    current_state = (random.uniform(-5, 5), random.uniform(-5, 5))
    current_energy = obj_func(*current_state)
    best_state = current_state
    best_energy = current_energy
    for i in range(num_iter):
        temperature = init_temp * math.exp(-alpha * i)
        new_state = (random.uniform(-5, 5), random.uniform(-5, 5))
        new_energy = obj_func(*new_state)
        delta_energy = new_energy - current_energy
        if delta_energy < 0:
            current_state = new_state
            current_energy = new_energy
        else:
            acceptance_prob = math.exp(-delta_energy / temperature)
            if random.random() < acceptance_prob:
                current_state = new_state
                current_energy = new_energy
        if current_energy < best_energy:
            best_state = current_state
            best_energy = current_energy

    return best_state, best_energy
# 这里调用了模拟退火算法
best_state, best_energy = simulated_annealing(rosenbrock, init_temp=100, alpha=0.01, num_iter=1000)

模拟退火在求解QUBO表达式中的应用

介绍了模拟退火的用法，我们来进一步介绍其在QUBO表达式求解中的应用。

QUBO是Quadratic Unconstrained Binary Optimization的简称，是一个二进制变量的函数优化问题。

下面我们就演示如何使用模拟退火解决QUBO问题:

想要利用模拟退火解决QUBO问题，首先需要我们明确QUBO的代价函数，我们需要根据实际情况来决定。
其次我们需要一个函数来生成一个相邻状态（在本问题中是附近的解），这在模拟退火中很重要。
最后我们利用模拟退火算法，将QUBO和约束表达式代入后即可求得结果。

首先我们来看代价函数部分的代码：

def QUBO_cost(Q, s):
    """
    计算QUBO表达式的代价函数
    Q: QUBO矩阵
    s: 二进制向量
    """
    cost = 0.0
    for i in range(len(s)):
        for j in range(len(s)):
            cost += Q[i][j] * s[i] * s[j]
    return cost

然后是求近邻状态的代码，这里是随机生成了一个临近的解，如下：


def neighbor(s):
    """
    生成一个邻居状态
    s: 二进制向量
    """
    n = len(s)
    i = np.random.randint(0, n)
    s_new = s.copy()
    s_new[i] = 1 - s_new[i]
    return s_new

最后是利用模拟退火进行求解的代码，主要按照下面的顺序进行：

随机生成初始状态
记录最优状态
计算最优代价
初始化温度
生成邻居状态
计算邻居状态的代价
降温

整个过程都会受到参数的影响，并且根据迭代次数循环上述过程，达到循环次数为止：

def simulated_annealing(Q, max_iter=10000, init_temp=100, cooling_rate=0.99):
    """
    利用模拟退火求解QUBO表达式
    Q: QUBO矩阵
    max_iter: 最大迭代次数
    init_temp: 初始温度
    cooling_rate: 降温速率
    """
    n = len(Q)
    s = np.random.randint(0, 2, n) # 随机生成初始状态
    s_best = s.copy() # 记录最优状态
    cost_best = QUBO_cost(Q, s_best) # 计算最优代价
    temp = init_temp # 初始化温度
    for i in range(max_iter):
        s_new = neighbor(s) # 生成邻居状态
        cost_new = QUBO_cost(Q, s_new) # 计算邻居状态的代价
        delta_cost = cost_new - cost_best
        if delta_cost < 0 or np.exp(-delta_cost / temp) > np.random.rand():
            s = s_new
            cost_best = cost_new
            if cost_best < QUBO_cost(Q, s_best):
                s_best = s.copy()
        temp *= cooling_rate # 降温
    return s_best, cost_best