注意事项:
状压dp难度警告!
本题为"状态压缩dp—蒙德里安的梦想"的近似题,建议先阅读这篇文章并理解。
题目:
在 n×n 的棋盘上放 k 个国王,国王可攻击相邻的 8 个格子,求使它们无法互相攻击的方案总数。
输入格式
共一行,包含两个整数 n 和 k。
输出格式
共一行,表示方案总数,若不能够放置则输出0。
数据范围
1≤n≤10,
0≤k≤n^2
输入:
3 2
输出:
16
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 12, M = 1 << 10, K = 110;
int n, m; //棋盘大小n*n, 有m个国王,
long long f[N][K][M]; //f[i][j][k],对于前i层的棋盘,总共放了j个国王,且第i层的状态为k(比如k是0101,1表示放了国王,0表示没放)的方案,
int c[M]; //count[i]为第i层国王的数量,
vector<int> state; //state存储所有合法状态,
vector<int> state_trans[M]; //state_trans[a] = {b1, b2, b3}存储能从合法状态a转移到的合法状态b,
bool check(int s) { //检查当前状态(二进制)是否存在连续的两个1,存在返回false不合法,不存在返回true合法。
for (int i = 0; i<n; i++) {
if ((s >> i & 1) && (s >> (i+1) & 1)) return false;
}
return true;
}
int count(int s) { //统计当前状态(二进制)中存在多少个1,也就是找到当前行中国王的个数。
int res = 0;
for (int i = 0; i<n; i++) res += (s >> i & 1);
return res;
}
int main() {
cin >> n >> m;
//预处理所有合法方案
for (int i = 0; i < (1<<n); i++) {
if (check(i)) { //如果当前状态合法,存入state,并计算状态中国王的数量。
state.push_back(i);
c[i] = count(i);
}
}
//预处理所有合法状态可以转移到的合法状态, 满足两种情况即可转移:
//1.状态a和状态b的&,为0,代表不存在交集, (比如01001和01010,&后就是01000,还有1存在说明肯定有两个国王会相互攻击到)
//2.状态a和状态b的|,不能存在两个连续的1,也就是需要转移后的方案是合法方案,
for (auto &a : state){
for (auto &b : state) {
if ((a&b)==0 && check(a|b)) {
state_trans[a].push_back(b); //符合两个条件,就说明能够从a转移到的状态b
}
}
}
//dp
f[0][0][0] = 1; //初始化,对于前0行,总共摆放了0个国王,且第0行的状态为0(一个都没摆),是一种合法方案。
for (int i = 1; i<=n+1; i++) { //枚举棋盘的每一行(枚举到n+1行是一个小优化)
for (int j = 0; j<=m; j++) { //枚举国王数量
for (auto &a : state) { //枚举合法状态a
for (auto &b : state_trans[a]) { //枚举所有能够从a转移到的状态b
if (j - c[a] >= 0) { //如果当前剩余的国王足够摆放,就可以进行状态更新
f[i][j][a] += f[i-1][j-c[a]][b];
}
}
}
}
}
//这里就将枚举到n+1行的优化体现出来了,f[n+1][m][0]代表,对于前n+1行,总共摆放了m个国王,且第i+1行的状态为0(一个都没摆),
//那其实也就代表了前i行摆了m个国王的总方案数。
cout << f[n+1][m][0];
return 0;
}
思路:
激动人心的状压dp来了(哭),还是经典的y式dp法
1.状态表示
f[i][j][k]:
对于棋盘的前i行(包括第i行)中,已摆放j个国王,并且第i行的状态为k的方案数,
属性为Count,
(这里的状态为k指的是二进制表示一行中"国王所在的位置",例如0101,就是在第2,4格子上分别有一个国王,换算为10进制就是5,是状态压缩dp中常用的存储状态的方法)
2.状态计算
一,首先来想一下什么状态(一行)是合法的呢?
也就是对于同一行来说,国王和国王之间最少保持一格距离为合法的状态。
(图是借的彩铅大佬的,绿色是国王,红色是攻击范围):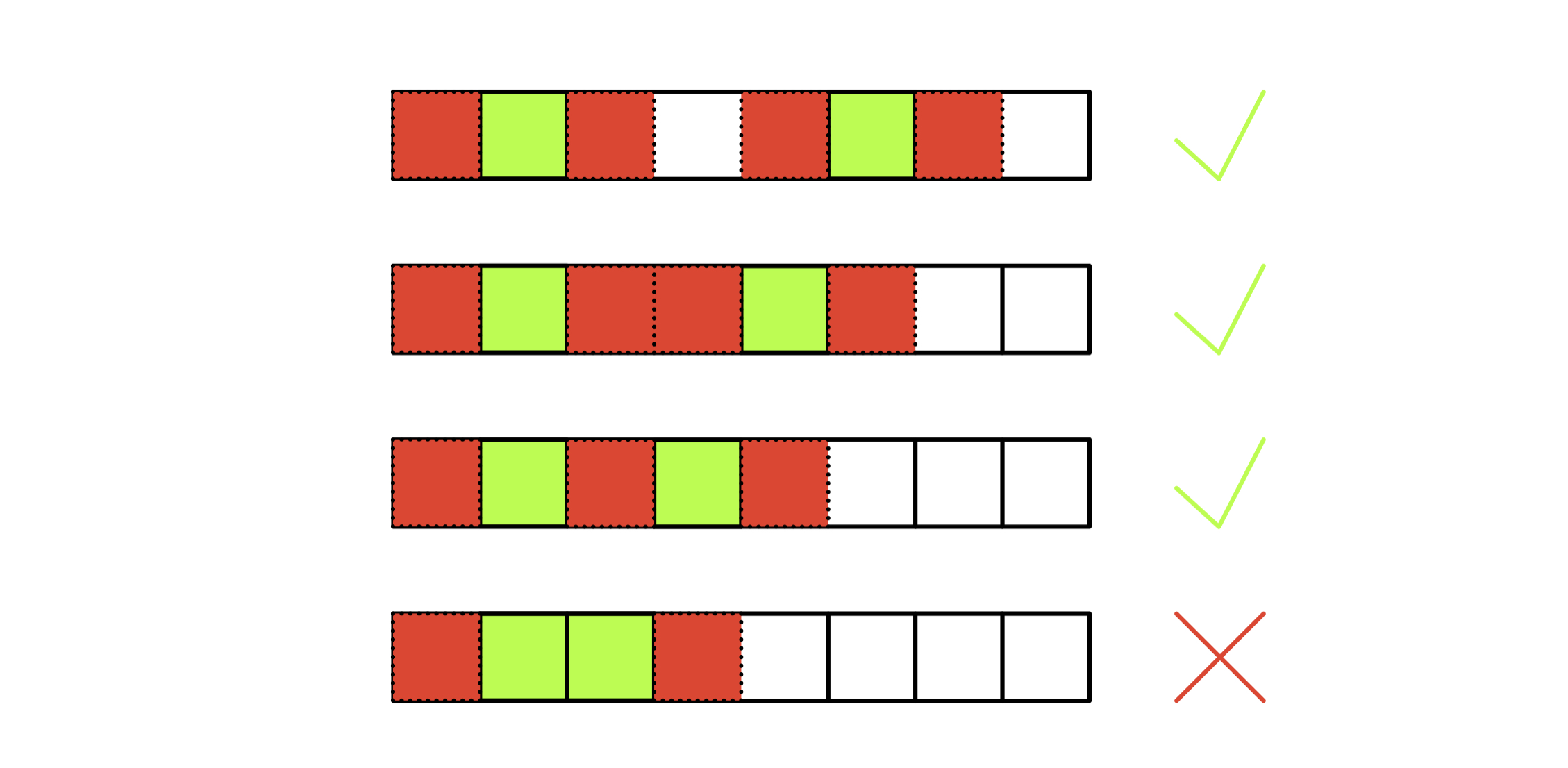
二,那再来想一下什么情况下进行状态更新(两行)是可行的呢?
也就是当a和b两个状态都是合法的前提下,
1.a和b的与运算等于0,(也就是a和b不能在相同位置上都有国王)
2.a和b的或运算的结果不存在连续的国王,(也就是结果是合法状态)
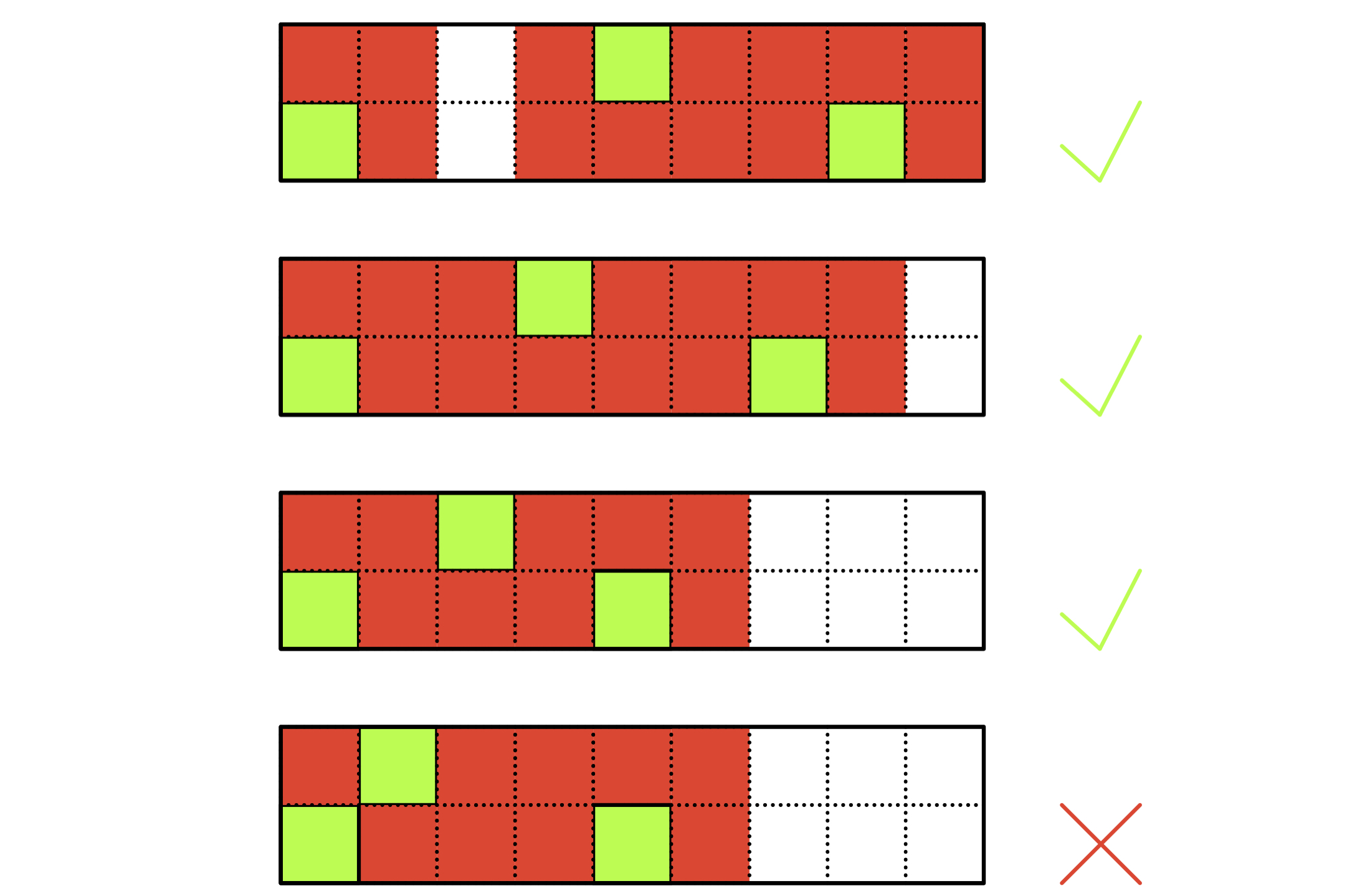
符合上述几个条件之后,终于可以进行状态转移了:
f[i][j][a] += f[i-1][j-c[a]][b]
直接从实际意义解释:
—第i行,棋盘上总摆放的国王数量为j,且第i行的状态为a,
可以从
—第i-1行,棋盘上总摆放的国王数量为"总国王数量 - 状态a的国王数量",且第i行的状态为b,
进行叠加转移。
如果有所帮助请给个免费的赞吧~有人看才是支撑我写下去的动力!
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流