1. 剑指 Offer 60. n 个骰子的点数

1.1 题目

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。

你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

示例 1:
    输入: 1
    输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]

示例?2:
    输入: 2
    输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
?

限制：
    1 <= n <= 11

1.2 解题思路

n个骰子想掷出点数i，需要第n个骰子掷出点数x，前n-1个骰子一共掷出点数i-x。因此n个骰子出现点i的概率记作dp[n][i],则dp[n][i+1]=dp[n-1][i-x] * dp[1][x]。
而dp[1][x]=1/6。所以可直接将状态转移公式写为dp[n][i+1]=dp[n-1][i-x]/6.0。
因此，最直接的思路可以定义一个二维数组，根据上一行的结果确定该行的概率结果。

1.3 数据类型功能函数总结

//二维数组相关操作
double[][] name=new double[line_size][row_size];//定义。

1.4 java代码

class Solution {
    public double[] dicesProbability(int n) {
        double[][] dp=new double[n+1][6*n+1];//行--n，列--n~6*n，保证下标和骰子编号对应
        int i,j;
        for(i=1;i<=6;i++){
            dp[1][i]=1.0/6.0;
        }
        for(i=2;i<=n;i++){//处理每一行
            for(j=1;j<i;j++){
                dp[i][j]=0;
            }
            for(j=i;j<=n*6;j++){//处理每一列 2,3,4,5,6,7,8,9,10,11,12
                for(int k=1;k<=6;k++){//
                    if(j-k>=i-1){
                        dp[i][j]+=dp[i-1][j-k]/6.0; //dp[1][1] dp[1][2] dp[1][3]
                    }
                }
            }
        }
        //获取最后一行的结果。
        double[] re=new double[5*n+1];
        for(i=n,j=0;i<=6*n;i++,j++){
            re[j]=dp[n][i];
        }
        return re;
    }
}

1.5 踩坑小记

1、计算出来的概率在最后一位总是比结果值大1；
原因在于我将1个骰子投出的结果按照输出样例的格式，写成1.6667(小数形式)而不是1/6的分式。
导致后面的运算过程中计算的是1.6667*1.6667而不是1/6*1/6的结果。
虽然刚开始这点误差没有什么，但是随着骰子数目增多，这样的误差会影响结果的数值。

修改的方式也很简单，将小数形式都改成分数形式即可。

1.6 进阶做法

根据官方题解的思路，dp[n][]的求解实际上只依赖于dp[n-1][]的6个元素值，因此，我们可以只定义两个一维数组，用类似于“滚动数组”的方式来写。

class Solution {
    public double[] dicesProbability(int n) {
        double[] dp=new double[6];//
        int i,j;
        //处理初始值
        for(i=0;i<6;i++){
            dp[i]=1.0/6.0;
        }
        for(i=2;i<=n;i++){//骰子数不断增加，i表示当前骰子数量
            double[] dp_new= new double[5*i+1];//新的结果数量为6*i-(i-1)=5*i+1;
            for(j=0;j<dp.length;j++){
                for(int k=0;k<6;k++){//每个元素项等于若干项之和
                //这两个for循环对应了dp_new中所有的结果情况，妙啊
                    dp_new[j+k]+=dp[j]/6.0;
                }
            }
            dp=dp_new;
        }
        return dp;
    }
}

不过我发现，使用1.4的一般解法，反而空间利用更少，而下面的进阶做法，空间利用更大了。
如图是1.4 一般做法的提交结果

如图是1.6 进阶做法的提交结果

总之就是很迷，不知道有没有大佬能解释这个现象。

2. 剑指 Offer 63. 股票的最大利润

2.1 题目

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

示例 1:
    输入: [7,1,5,3,6,4]
    输出: 5
    解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:
    输入: [7,6,4,3,1]
    输出: 0
    解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

限制：
    0 <= 数组长度 <= 10^5

2.2 解题思路

最简单的思路：买卖一次股票，查找最小值买入，在最小值之后的数据中查找最大值_但是存在次优解的情况，所以这种思路pass.

使用动态规划，则假设dp[i]表示第i天为止的最低卖出价格，最大利润为price[i]-dp[i]。
状态转移方程设计如下：

• 如果price[i]<dp[i]，表示买入价格可更低，dp[i]=price[i];表示更新买入
• price[i]>dp[i]，表示可以卖出，则dp[i]=dp[i-1]，考虑卖出之后的利润是不是最大的。

为了降低空间复杂度，本题中dp[i]只和dp[i-1]有关，所以只需要设置一个整型数字即可。profit变量总是在可卖出的时候记录当前最大的卖出利润，也可以理解为一个动态规划问题。

这种思路和官方的解题思路异曲同工，官方解法里面cost是本思路中的dp[i],官方题解中的dp[i]是本思路中的profit.

2.3 数据类型功能函数总结

//none

2.4 java代码

class Solution {
    public int maxProfit(int[] prices) {
        int profit=0;
        if(prices.length==0){return 0;}
        int dp=prices[0];
        for(int i=1;i<prices.length;i++){
            if(prices[i]<dp){//更新买入
                dp=prices[i];
            }
            else{//考虑卖出
                if(prices[i]-dp>profit){
                    profit=prices[i]-dp;
                }
            }
        }
        return profit;  
    }
}

3. 剑指 Offer 12. 矩阵中的路径

3.1 题目

给定一个m x n 二维字符网格board 和一个字符串单词word 。如果word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1：
    输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
    输出：true
示例 2：
    输入：board = [["a","b"],["c","d"]], word = "abcd"
    输出：false

提示：
    m == board.length
    n = board[i].length
    1 <= m, n <= 6
    1 <= word.length <= 15
    board 和 word 仅由大小写英文字母组成

3.2 解题思路

个人思路是从起点开始，每次往四个方向查找，如果都没有合适的则默认一个特定的顺序进行四周的搜索，找到第一个字符之后，继续查找，为了回溯设置一个查找标记的矩阵，和board对应。
结合官方题解，主要解决了我在这个思路中的三个疑问：

• 如何查找到第一个元素：根据官方题解和代码参考，地毯式遍历行列中的元素，如果以某个元素为起点进行搜索得到了最终的结果，则说明矩阵中有字符串，否则则在所有元素遍历完成之后说明矩阵中没有该字符。
• 如何进行遍历和方向搜索：官方题解中给出了DFS深度优先搜索算法，并且使用递归的方式来实现。终止条件设置为越界或者字符不匹配的时候或者查找结束之后，而递归部分分别查找上下左右四个方位，只要有一个方向能走得下去即可。
• 如何进行矩阵元素标记和回溯：为了节省空间，可考虑直接修改矩阵内元素而不是另外开辟一块空间；遍历过的元素则修改为"\0"字符，如果遍历搜索失败，需要回溯，则使用word字符串的当前搜索位置还原被标记的元素。
  DFS算法的递归实现是核心重点。

3.3 数据类型功能函数总结

//二维数组相关操作
int line=array_name.length;//获取行数
int row=array_name[0].length;//获取列数
//字符串相关操作
String.length();//获取字符串长度
String.charAt(index);//获取某个下标的对应字符。

3.4 java代码

class Solution {
    public boolean exist(char[][] board, String word) {
        int i=0,j=0,index=0;;
        int line=board.length;
        int row=board[0].length;
        for(i=0;i<line;i++){
            for(j=0;j<row;j++){
                if(dfs(board,word,i,j,0)==true){
                    return true;
                }
            }
        }
        return false;
    }
    boolean dfs(char[][] board,String word,int i,int j,int k){//递归函数
        if(i >=board.length || j >= board[0].length || j<0||i<0||board[i][j]!=word.charAt(k)){
            return false;
        }
        if(k==word.length()-1){
            return true;
        }
        board[i][j]='\0';
        boolean re=dfs(board,word,i+1,j,k+1)||dfs(board,word,i-1,j,k+1)||dfs(board,word,i,j+1,k+1)||dfs(board,word,i,j-1,k+1);
        board[i][j]=word.charAt(k);
        return re;
    }
}

4. 剑指 Offer 13. 机器人的运动范围

4.1 题目

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：
    输入：m = 2, n = 3, k = 1
    输出：3

示例 2：
    输入：m = 3, n = 1, k = 0
    输出：1

提示：
    1 <= n,m <= 100
    0 <= k?<= 20

4.2 解题思路

和矩阵中的路径类似，需要考虑的是矩阵中的搜索问题，因此还是使用dfs搜索进行矩阵遍历。

终止条件：达到边界或者行坐标和列坐标位数大于k，n和m最大也是二位数。
递归部分：左、右、上、下进行搜索，每次搜索到一个格子，进行格子统计。

后来经过代码测试和题解的提示，首先需要设置访问矩阵记录访问过的元素值，从而避免同一个单元格多次统计；还有就是由于解的区域是三角形，可以仅考虑搜索右下方向来进行矩阵搜索。【很有意思的点，如果直接四个方向访问的话，会出现栈溢出的情况】

4.3 数据类型功能函数总结

//数组相关操作
int[] array_name=new int[]{初始的元素值};//数组定义方式1
int[] array_name=new int[len];//数组定义方式2
//矩阵相关操作
int[][] array_name=new int[line_len][row_len];//矩阵定义
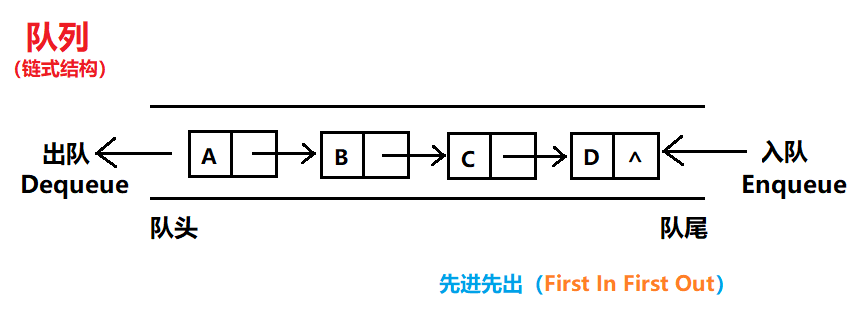
//队列相关操作
LinkedList<> queue_name=new LinkedList<>();//队列结构用linkedlist实现
queue_name.add();//添加元素
queue_name.poll();//弹出元素
queue_name.size();//获得队列大小

4.4 java代码

class Solution {
    int m,n,k;
    int[][] visited;
    public int movingCount(int m, int n, int k) {
        int re=1;
        visited=new int[m][n];
        re=dfs(m,n,k,0,0);
        return re;
    }
    public int dfs(int m, int n, int k,int i,int j) {
        if(i>=m||j>=n||i<0||j<0||i%10+i/10+j%10+j/10>k||visited[i][j]==1){
            return 0;
        }
        else{
            visited[i][j]=1;
            int re=1;
            re+=dfs(m,n,k,i+1,j)+dfs(m,n,k,i,j+1);
            return re;
        }
    }
}

4.5 另解

搜索回溯类的问题另外一种解法思路是广度优先遍历，深度优先遍历DFS需要借助栈结构，可递归实现，对应的，广度优先遍历需要借助队列结构。

class Solution {
    int m,n,k;
    int[][] visited;
    LinkedList<int[]> queue=new LinkedList<int[]>();//队列结构
    public int movingCount(int m, int n, int k) {
        int re=0;
        visited=new int[m][n];
        //广度优先遍历
        queue.add(new int[]{0,0});//初始的i，j
        while(queue.size()!=0){
            int[] temp=queue.poll();
            int i=temp[0],j=temp[1];
            if(i<m && j<n && i>=0 && j>=0 && (i/10+i%10+j/10+j%10)<=k && visited[i][j]!=1){
                re++;//统计到达的格子
                queue.add(new int[]{i+1,j});
                queue.add(new int[]{i,j+1});
                visited[i][j]=1;
            }
        }
        return re;
    }
}

又是只完成一半任务的一周（衰