以下课程来源于MOOC学习—原课程请见：数据库原理与应用
考研复习

引言

设计的时候:

我们为什么不能设计成R（学号，课程号，姓名，所咋系，系主任，成绩）？

因为存在数据冗余（存在姓名。所在系，系主任的信息冗余）

因为存在更新异常（无法插入学生信息，系的信息；无法删除学生选课信息）

比如添加学生信息无法添加选课信息，删除学生选课信息可能造成该课程不存在

因为存在数据不一致（修改学生系信息，出现系相同主任不同的情况等）

函数依赖

定义：设 R 为任一给定关系，如果对于 R 中属性 X 的每一个值，R 中的属性 Y 只有唯一值与之对应，则称 X 函数决定 Y 或称 Y 函数依赖于 X ，记作 X—>Y。其中，X 称为决定因素。

通俗一点，就是给定一个 X 都有唯一的 Y。可以理解为函数 y = f(x);

对于任意的 x 都有唯一的 y ，且 y 的取值由 x 决定。

例如：学生号—>学生姓名，学生年龄等等有关该学生的所有信息
反之，像学生姓名不能决定唯一的学生，因为存在同名的可能，这种情况就不能称作函数依赖。或者学生学号确定后，却不能确定课程编号，因为一对多

根据函数依赖性质可分为以下三种：

完全函数依赖记F
- 书上定义基本是：如果存在 X 属性集（注意是集合，说明是联合主键）决定唯一的 Y ，且 X 中的任一子集都不能决定唯一的 Y，则 Y 完全依赖于 X。
- 例如：学生数学成绩完全由该学生的学号和数学课决定，所以数学课成绩完全依赖于（学号，数学课）
部分函数依赖记P
- 定义和完全函数依赖有一点不一样，就是 X 的属性集中任一子集可以决定唯一的 Y
- 例如：学生学号和姓名可以决定唯一的学生，但是学生号也可以决定唯一的学生
传递函数依赖记t
- 定义：设 R 为任一关系， X Y Z 为其不同的属性子集，若 X —> Y, Y 不决定 X 且 Y —>Z，则有 X —>Z，称为 Z 传递函数依赖于 X
- 例如：书的出版编号是唯一，版权归出版社所有，所以只能由该出版社出版。所以存在函数依赖：书出版编号—>出版社名，出版社名—>出版社地址，但是出版社名不能决定唯一的出版书编号（除非出版社只出版过一本书，那我没话说?），则有出版社地址传递函数依赖于出版书编号
平凡函数依赖
- 设 R 为任一关系， X 属于U，Y属于U，且Y属于X，若X->Y成立，称
- 例如：(学号，姓名)-> 姓名

候选键

定义1：关系R中某一属性或者属性组K的值可以唯一标识一个元组，而其**任意真子集**不可以，则K为候选键（码）

定义2：关系模式R(U)中，k∈U，且U完全依赖于K

比如有关系模式 R (Sno, Sname, Cno, Cname, Sdept, Sloc, Grade)，

其中函数依赖集为 F= {Sno → Sname, Sno → Sdept, Sdept → Sloc，Sno → Sloc, Cno → Cname, (Sno, Cno) → Grade }

那么 R 中的码只能是 (Sno, Cno)，Sno 或 Cno 并不能唯一标识一个数据（其实就是不能决定 Grade )，所以单独的 Sno 与 Cno 并不能作为码。

所以可得到主属性：Sno, Cno
；非主属性：Sname, Cname, Sdept, Sloc, Grade

因此：

R（学号，课程号，姓名，所咋系，系主任，成绩）

（学号，课程号）-f->成绩（学号，课程号）-p->姓名

（学号，课程号）-p->所在系（学号，课程号）-t->系主任

第一范式1NF

范式：

数据依赖满足一定约束。

补充：关系可以理解为数据表。“关系模式”和“关系”的区别，类似于面向对象程序设计中”类“与”对象“的区别。”关系“是”关系模式“的一个实例，你可以把”关系”理解为一张带数据的表，而“关系模式”是这张数据表的表结构。

第一范式：符合1NF的关系中的每个属性都不可再分。

1NF是所有关系型数据库的最基本要求

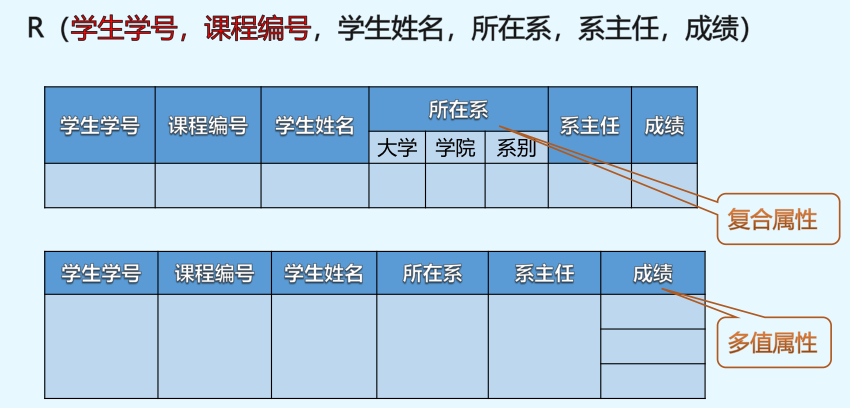
举例：根据定义R（学号，课程号，姓名，所咋系，系主任，成绩）符合∈1NF

第二范式2NF

2NF在1NF的基础之上，消除了非主属性对于码的部分函数依赖

定义：第一范式基础上，每个非主属性完全依赖于候选键

但是例子中：（学号，课程号）-p->姓名（学号，课程号）-p->所在系

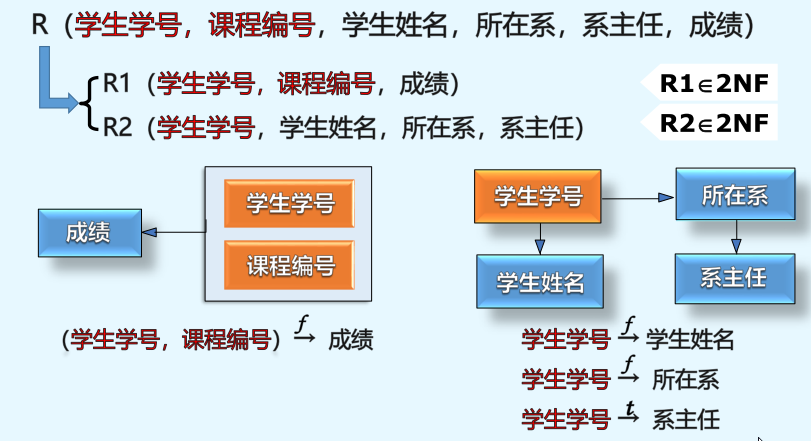
分解后解决了数据冗余的问题和更新异常的问题

但是仍然存在非主属性系主任对于码学号的传递函数依赖

第三范式3NF

3NF在2NF的基础之上，消除了非主属性对于码的传递函数依赖

定义：第二范式基础上，所有非主属性不存在传递依赖于候选键

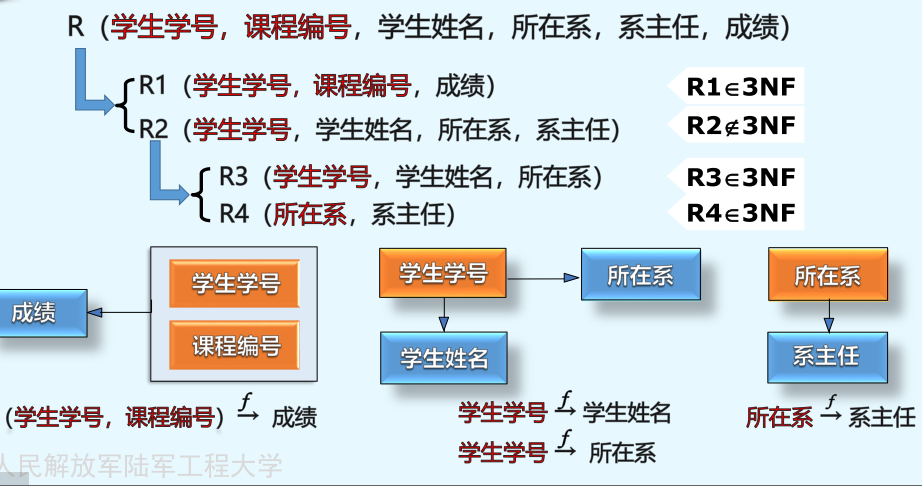
由此可见，符合3NF要求的数据库设计，基本上解决了数据冗余过大，插入异常，修改异常，删除异常的问题。当然，在实际中，往往为了性能上或者应对扩展的需要，经常做到2NF或者1NF，但是作为数据库设计人员，至少应该知道，3NF的要求是怎样的。

BCNF

问题：

某公司有若干个仓库；每个仓库只能有一名管理员，一名管理员只能在一个仓库中工作；
一个仓库中可以存放多种物品，一种物品也可以存放在不同的仓库中。每种物品在每个仓库中都有对应的数量。

那么关系模式仓库（仓库名，管理员，物品名，数量）属于哪一级范式？

答：已知函数依赖集：仓库名 → 管理员，管理员 → 仓库名，（仓库名，物品名）→ 数量
码：（管理员，物品名），（仓库名，物品名）

主属性：仓库名、管理员、物品名 非主属性：数量

∵ 不存在非主属性对码的部分函数依赖和传递函数依赖。
∴ 此关系模式属于3NF。
基于此关系模式的关系（具体的数据）可能如图所示：

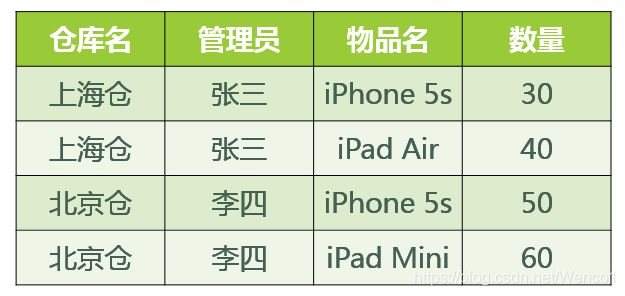
好，既然此关系模式已经属于了 3NF，那么这个关系模式是否存在问题呢？

我们来看以下几种操作：

1.先新增加一个仓库，但尚未存放任何物品，是否可以为该仓库指派管理员？——不可

因为物品名也是主属性，根据实体完整性的要求，主属性不能为空。

2.某仓库被清空后，需要删除所有与这个仓库相关的物品存放记录，会带来什么问题？——仓库本身与管理员的信息也被随之删除了。

3.如果某仓库更换了管理员，会带来什么问题？——这个仓库有几条物品存放记录，就要修改多少次管理员信息。

从这里我们可以得出结论，在某些特殊情况下，即使关系模式符合 3NF 的要求，仍然存在着插入异常，修改异常与删除异常的问题，仍然不是 ”好“ 的设计。
造成此问题的原因：存在着主属性对于码的部分函数依赖与传递函数依赖。（在此例中就是存在主属性【仓库名】对于码【（管理员，物品名）】的部分函数依赖。

解决办法就是要在 3NF 的基础上消除主属性对于码的部分与传递函数依赖。

仓库（仓库名，管理员）
库存（仓库名，物品名，数量）

这样，之前的插入异常，修改异常与删除异常的问题就被解决。
以上就是关于 BCNF

总结

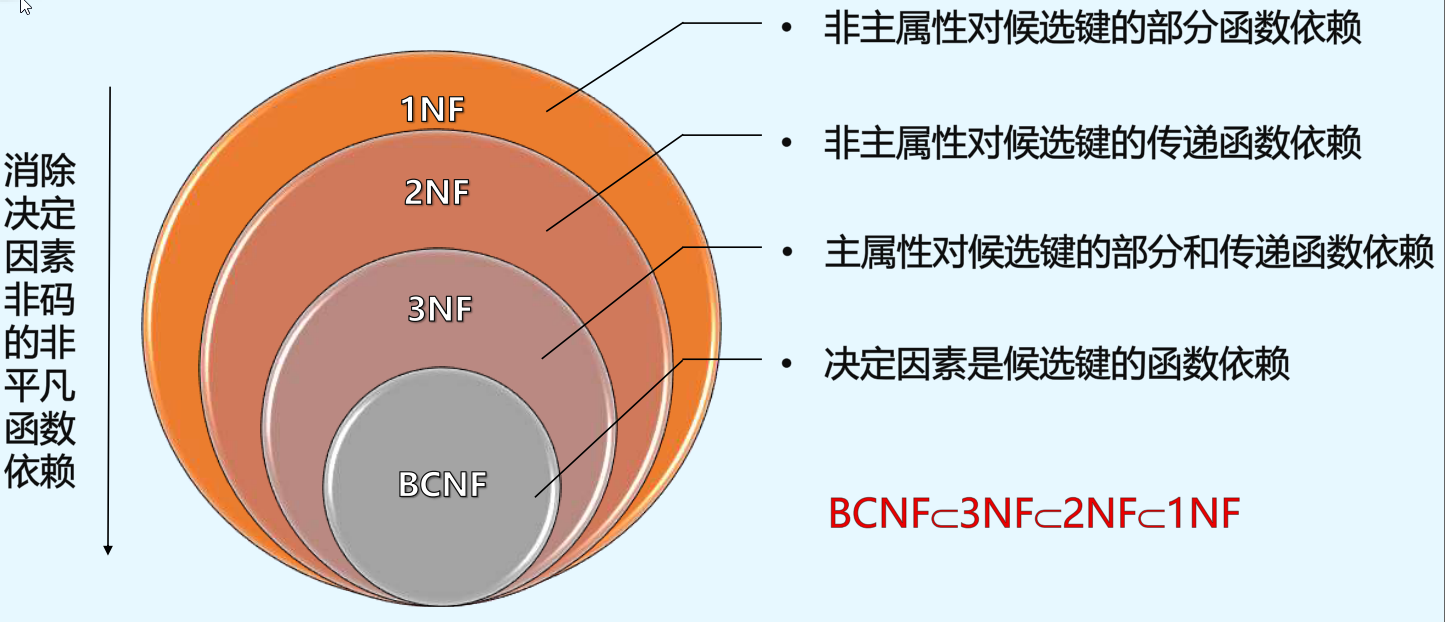
Armstrong公理

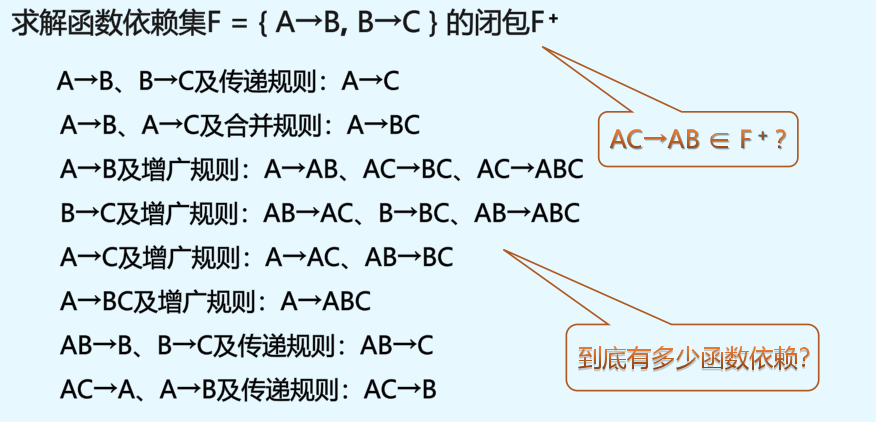
引出：我们能否根据给定的依赖集推出完整的函数依赖集

逻辑蕴含

定义：F是关系模式R 的函数依赖集，X,Y是R 的属性子集，对于R 满足F的关系实例（一行数据）r，如果X->Y都成立，称为F逻辑蕴含X->Y

俗话：每行数据的属性X都能推出Y，则

F逻辑蕴含的所有函数依赖的集合（所有函数依赖），称为函数依赖集记F+

目的：根据给定的（部分）依赖集推出完整的函数依赖集

补充：XY记为X和Y 的并集

基本推理规则

关系R(U,F) U是属性集

（1）自反律：若Y包含于X，X包含于U，则X->Y为F所蕴含。

（2）增广律：若X->Y为F所蕴含，且Z包含于U，则XZ->YZ为F所蕴含。

（3）传递律：若X->Y及Y->Z为F所蕴含，则X->Z为F所蕴含。

注：为F所蕴含 === 是函数依赖集的一部分

根据上面三条推理规则可以得到下面三条推理规则：

（1）合并规则：由X->Y, X->Z，有X->YZ

（2）伪传递规则:由X->Y，WY->Z，有XW->Z

（3）分解规则：由X->Y及Z包含于U，有X->Z

引理：X->A1A2A3A4…成立的充要条件 X->Ai都成立

属性集闭包

忽略

闭包：闭包就是由一个属性直接或间接推导出的所有属性的集合

例（1）：设有关系模式R(U，F)，其中U={A，B，C，D，E，I}，F={A→D，AB→E，BI→E，CD→I，E→C}，计算(AE)+

解: (1) 令X={AE}，X(0)=AE

(2)在F中寻找尚未使用过的左边是AE的子集的函数依赖，结果是: A→D， E→C；所以 X(1)=X(0)DC=ACDE，显然 X(1)≠X(0).

(3) 在F中寻找尚未使用过的左边是ACDE的子集的函数依赖，结果是: CD→I；所以 X(2)=X(1)I=ACDEI。虽然X（2）≠X(1)，但F中寻找尚未使用过函数依赖的左边已经没有X（2）的子集，所以不必再计算下去，即(AE)+=ACDEI。

例如：f={a->b，b->c，a->d，e->f}；由a可直接得到b和d，间接得到c，则a的闭包就是{a，b，c，d}

函数依赖集等价

F，G是一个关系模式的两个函数依赖集，如果F+=G+，则称F和G 是等价的

F={AB->C,A->B,B->A} G={A->C,A->B,B->A}

充要条件：一个函数的依赖集F+属于另一个函数依赖集G+的子集

(考察 F+中每个函数依赖是否在G+中，同理)

最小函数依赖集

如果函数依赖的集合满足一下称为：

1.对于函数依赖的右端，将其分解为单个属性。如AB->CD分解为AB->C,AB->D

2.对于函数依赖集F中每一个X->A,计算G=F-{X->A},

判断是否A∈(X)G+ 如果能，在F中删除X->A。

3.对于函数依赖集F中每一个X->A,设X=B1B2B3…

判断是否A∈(X-Bi)F+，如果能，X=X-Bi

https://blog.csdn.net/liudongdong19/article/details/85223697

同理推：5-4 F={A->BC,B->AC,C->A} 结果：Fm={A->B,B->C,C->A}

候选键的判定

关系模式中R(U,F)中，如果K∈U，且U**完全依赖**于K，

U是完全依赖K，不能依赖于K 的任何子集 K才能是候选键

利用Armstrong公理

需要熟练掌握Armstrong

※根据闭包的概念

第一种：因为：U是完全依赖K，不能依赖于K 的任何子集

或者以下重要方法：

※计算候选码的方法

对于给定的关系R（A1，A2，…An）和函数依赖集F，可将其属性分为4类：

L类仅出现在函数依赖左部的属性。

R 类仅出现在函数依赖右部的属性。

N 类在函数依赖左右两边均未出现的属性。

LR类在函数依赖左右两边均出现的属性。

定理：对于给定的R及其函数依赖集F，若X(X∈R)是L类属性，则X必为R的任一候选码的成员

推论：若X(X∈R)是L类属性，且X+包含了R的全部属性；则X必为R的唯一候选码。

例（2）：设有关系模式R（A，B，C，D），其函数依赖集F={D→B，B →D，AD →B，AC →D}，求R的所有候选码。

解：考察F发现，A，C两属性是L类属性，所以AC必是R的候选码成员，又因为（AC）+=ABCD，所以AC是R的唯一候选码。

定理：对于给定的R及其函数依赖集F，若X（X∈R）是R类属性，则X不在任何候选码中。

定理：对于给定的R及其函数依赖集F，若X（X∈R）是N类属性，则X必包含在R的任一候选码中

推论：对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类和N类组成的属性集，且X+包含了R的全部属性；则X是R的唯一候选码。

模式分解

低级模式向高级模式分解比如1NF---->3NF

将一关系模式R(U,F)分解，成多个关系模式（表），并且各个关系模式（表）的属性并集仍为U，各个关系模式（表）的属性集并不包含，每个关系模式的依赖是在F上的投影

特性：保持了函数依赖，具有无损连接性

关系模式分解的无损连接性和保持函数依赖特性对应分解前后关系的（语义等价）和（数据等价）

数据等价是指分解前后的关系实例表示相同的信息内容，用（无损连接）特性来衡量。
语义等价是指分解前后的关系模式上的函数依赖集等价，即有相同的函数依赖集闭包，用（保持函数依赖）特性来衡量。
关系模式分解的无损连接和保持函数依赖两个特性之间（没有必然联系）。

为什么希望分解既具有无损连接性又要保持函数依赖？

分解具有无损连接性，即可保持数据等价，那分解之后得到的新关系就不会有信息内容的丢失。
分解保持函数依赖，即可保持函数依赖等价，那么分解之后数据的语义就不会出差错。

若分解保持函数依赖，模式总可以分解到3NF。
若分解具有无损连接性，模式一定能分解到BCNF。
若分解要保持函数依赖且具有无损连接性，模式可以分解到3NF。可以达到BCNF

但是BC范式的两个特性和BCNF的两个特性不能同时拥有

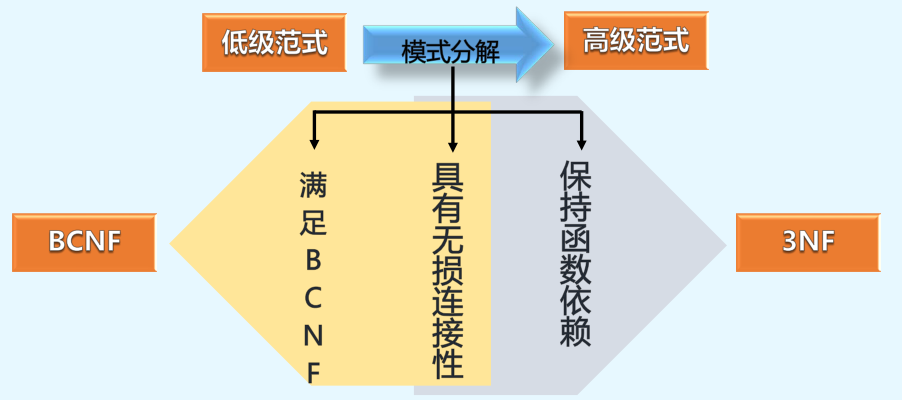
分解

原来的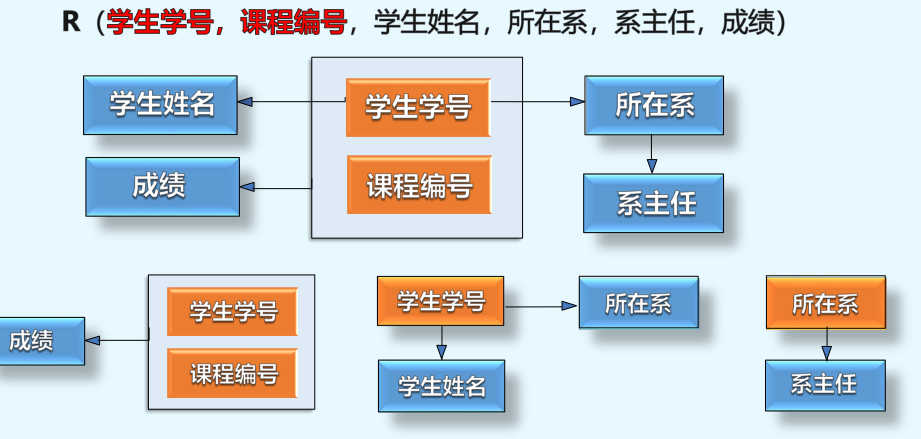

为了解决对学生信息，系信息，选修信息等新数据冗余，不一致，更新异常等问题，我们不断分解成如下的模式，由满足低级范式的模式逐步分解变成高一级的范式

分解后

分解后，三个关系的属性集没有包含关系，并集为关系R 的属性集，关系R 原有的函数依赖也投影到不同的关系模式上，如果对三个关系模式自然连接，可以回到原有的关系（数据表）

判断是否是无损连接

对于一个分解，有k个子集，n个属性，建立一张k行n列的初始表，对于每一行也就是分解的每个子集，把该分解子集出现的属性对应的列写上ajaj，否则写上bijbij
对于每一个依赖，找到左部属性对应的列，根据行的值分组，对于行的值相同的这些行，查看对应右部属性的列，如果这些格子里有a值，那把所有这些格子改成a值，如果没有，改成行最小的b值。如果某个b值改成a值，那么其他行(不属于当前操作的行)的相同b值也要改成a值。
如果不变则停止，如果出现有一行为a1 a2 … an，那么说明该连接为无损连接。
https://www.cnblogs.com/zxcoder/p/11963759.html

举例：

已知关系模式R(A，B，C，D，E，G)及R上的函数依赖集F={A→BC, C→D, BC→EG, E→A }，有R上的一个分解ρ={R1(A,B,C,D)，R2(B,C,E,G)}，则该分解( 具有无损连接性，但不保持函数依赖)。

已知关系模式R（A, B, C, D, E）及R上函数依赖集F＝{A→BC，C→D，BC→E，E→A｝，则分解ρ={R1（ABCE），R2（CD）｝满足（具有无损连接性、保持函数依赖）。