1.伪代码以及用到的公式

-

-

-

2.代码
package collection;
public class StrassenMatrixMultiplication {
public static int[][] multiply(int[][] a, int[][] b) {
int n = a.length;
int[][] result = new int[n][n];
if (n == 1) {
result[0][0] = a[0][0] * b[0][0];
} else {
int[][] a11 = new int[n / 2][n / 2];
int[][] a12 = new int[n / 2][n / 2];
int[][] a21 = new int[n / 2][n / 2];
int[][] a22 = new int[n / 2][n / 2];
int[][] b11 = new int[n / 2][n / 2];
int[][] b12 = new int[n / 2][n / 2];
int[][] b21 = new int[n / 2][n / 2];
int[][] b22 = new int[n / 2][n / 2];
// Divide matrices into sub-matrices of size n/2 x n/2
divide(a, a11, 0, 0);
divide(a, a12, 0, n / 2);
divide(a, a21, n / 2, 0);
divide(a, a22, n / 2, n / 2);
divide(b, b11, 0, 0);
divide(b, b12, 0, n / 2);
divide(b, b21, n / 2, 0);
divide(b, b22, n / 2, n / 2);
// Calculate p1 to p7
int[][] p1 = multiply(add(a11, a22), add(b11, b22));
int[][] p2 = multiply(add(a21, a22), b11);
int[][] p3 = multiply(a11, sub(b12, b22));
int[][] p4 = multiply(a22, sub(b21, b11));
int[][] p5 = multiply(add(a11, a12), b22);
int[][] p6 = multiply(sub(a21, a11), add(b11, b12));
int[][] p7 = multiply(sub(a12, a22), add(b21, b22));
// Calculate sub-matrices of result matrix
int[][] c11 = add(sub(add(p1, p4), p5), p7);
int[][] c12 = add(p3, p5);
int[][] c21 = add(p2, p4);
int[][] c22 = add(sub(add(p1, p3), p2), p6);
// Combine sub-matrices into result matrix
combine(c11, result, 0, 0);
combine(c12, result, 0, n / 2);
combine(c21, result, n / 2, 0);
combine(c22, result, n / 2, n / 2);
}
return result;
}
// Divide matrix into sub-matrices
public static void divide(int[][] parent, int[][] child, int i, int j) {
for (int m = 0, n = i; m < child.length; m++, n++) {
for (int p = 0, q = j; p < child.length; p++, q++) {
child[m][p] = parent[n][q];
}
}
}
// Combine sub-matrices into matrix
public static void combine(int[][] child, int[][] parent, int i, int j) {
for (int m = 0, n = i; m < child.length; m++, n++) {
for (int p = 0, q = j; p < child.length; p++, q++) {
parent[n][q] = child[m][p];
}
}
}
// Add two matrices
public static int[][] add(int[][] a, int[][] b) {
int n = a.length;
int[][] result = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
result[i][j] = a[i][j] + b[i][j];
}
}
return result;
}
// Subtract two matrices
public static int[][] sub(int[][] a, int[][] b) {
int n = a.length;
int[][] result = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
result[i][j] = a[i][j] - b[i][j];
}
}
return result;
}
}
3.原理
-
如果 n = 1,则每个矩阵包含一个元素。执行单个标量乘法和单个标量加法,就像 MATRIX-Multiply-RECURSIVE 的第3行那样,计算 Θ (1)的时间,然后返回。否则,将输入矩阵 A、 B 和输出矩阵 C 划分为 n/2 × n/2子矩阵,如方程(4.2)所示。这一步通过索引计算 Θ (1)的时间,就像在 MATRIX-Multiply-RECURSIVE 中一样。
-
创建 n/2 × n/2矩阵 S~1~,S~2~,... ,S~10~,每个矩阵都是步骤1中两个子矩阵的和或差。建立并归零七个 n/2 × n/2矩阵 P~1~,P~2~,... ,P~7~的条目以保持七个 n/2 × n/2矩阵乘积。所有17个矩阵都可以在 Θ (n2)时间内创建并初始化 P~i~
-
使用步骤1中的子矩阵和步骤2中创建的矩阵 S1,S2,... ,S10,递归地计算7个矩阵乘积 P~1~,P~2~,... ,P~7~中的每一个,花费7T (n/2)的时间。
-
对结果矩阵 C 的四个子矩阵 C11,C12,C21,C22进行修正,通过加减各种 P~i~ 矩阵来实现,这需要 Θ (n2)的时间。
假定一旦矩阵规模从n变为1,就进行简单的标量乘法计算,正如SQUARE-MATRIX-MULTIPLYRECURSIVE的第4行那样。当n>l时,步骤1、2和4共花费Θ(n2)时间,步骤3要求进行7次n/2Xn/2矩阵的乘法。因此,我们得到如下描述Strassen算法运行时间T(n)的递归式:

4.数学计算原理
步骤2,创建如下10个矩阵
10个矩阵:

由于必须进行10次n/2Xn/2矩阵的加减法,因此,该步骤花费8(n^2^)时间。
步骤3,递归地计算7次n/2*n/2矩阵的乘法

步骤4,对步骤3创建的P;矩阵进行加减法运算,计算出C的4个n/2* n/2的子矩阵.
C11 = C11 + P5 + P4-P2 + P6.

C~12~ = C~12~ + P~1~ + P~2~

C~21~ = C~21~ + P~3~ + P~4~

C22 = C22 + P5 + P1-P3-P7
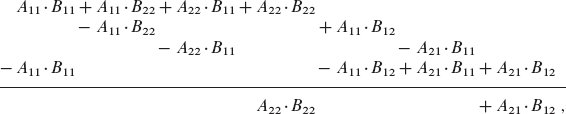
5.疑问
1.为什么要使用P1 到p7
用加减法来降低乘法的次数
在 Strassen 算法中,使用了七个中间矩阵 P1 到 P7 来计算矩阵乘积,具体原因如下: 为了避免重复计算,需要将输入的两个矩阵分别拆分成四个小矩阵,然后将这些小矩阵用来计算中间矩阵 P1 到 P7。 中间矩阵 P1 到 P7 的计算方式是通过加减法来实现的,因此可以减少乘法的次数,从而减少计算量。 通过使用中间矩阵 P1 到 P7,可以将原来需要进行 8 次矩阵乘法的计算量减少到 7 次。 综上所述,使用中间矩阵 P1 到 P7 可以提高矩阵乘法的效率,减少计算量。
2.可以使用p1到p10吗
在 Strassen 算法中,使用中间矩阵 P1 到 P7 是该算法的核心思想之一,它们用于表示两个矩阵相乘的结果。通常情况下,使用七个中间矩阵是足够的,因为它们已经能够减少矩阵乘法的计算量,从而提高算法的效率。 虽然可以添加更多的中间矩阵,例如 P8、P9、P10 等,但是这样并不一定能够进一步提高算法的效率,反而可能会增加计算量和程序的复杂度。因此,使用七个中间矩阵 P1 到 P7 是 Strassen 算法的常规做法,也是较为有效的优化策略。
3.至于为什么c11,c12 是这样的表达式
在 Strassen 算法中,矩阵乘积的计算采用了递归的方式,将输入矩阵分解成多个子矩阵进行计算,最终将这些子矩阵合并得到矩阵乘积。
具体地说,对于两个 n×n 的矩阵 A 和 B,Strassen 算法将 A 和 B 分解成四个 n/2×n/2 的子矩阵,然后通过以下公式计算矩阵乘积 C = A × B:
C11 = P5 + P4 - P2 + P6 C12 = P1 + P2 C21 = P3 + P4 C22 = P5 + P1 - P3 - P7
其中,P1 到 P7 是中间矩阵,表示为:
P1 = A11 × (B12 - B22) P2 = (A11 + A12) × B22 P3 = (A21 + A22) × B11 P4 = A22 × (B21 - B11) P5 = (A11 + A22) × (B11 + B22) P6 = (A12 - A22) × (B21 + B22) P7 = (A11 - A21) × (B11 + B12)
在这个公式中,C11 表示乘积的左上角 n/2×n/2 的子矩阵,P5、P4、P2 和 P6 都是中间矩阵,它们通过加减法来计算 C11 的值。具体来说:
P5 表示 (A11 + A22) × (B11 + B22) 的结果,它包含 C11、C12、C21 和 C22 中的所有元素。 P4 表示 A22 × (B21 - B11) 的结果,它包含 C11 和 C21 中的所有元素。 P2 表示 (A11 + A12) × B22 的结果,它包含 C11 和 C12 中的所有元素。 P6 表示 (A12 - A22) × (B21 + B22) 的结果,它包含 C11 和 C21 中的所有元素。 因此,将这些中间矩阵相加减,可以得到 C11 的值。具体来说,C11 = P5 + P4 - P2 + P6。这个公式的含义是,将 P5、P4、P2 和 P6 中包含 C11 的部分相加减,可以得到 C11 的值。