在上一篇文章中,通过一个例子来说明最小二乘在拟合直线时所发挥的作用,也通过两个插图的比较进一步的阐明了投影与最小化e之间的密切关系。
线性代数 --- 最小二乘在直线拟合上的应用与Gram-Schmidt正交化(上)_松下J27的博客-CSDN博客本文接续上文,从最小二乘在直线拟合上的应用开始,一步步推导出什么是Gram-Schmidt正交化,以及为什么我们需要对矩阵A中的列向量进行正交化的处理https://blog.csdn.net/daduzimama/article/details/129995583 在这篇文章中,我们依然会从三组数据点的直线拟合开始,所不同的是,这次的三个观测点的值比较特殊,继而引出Gram-Schmidt正交化的概念。
Example 2:
在一个实验中的不同时刻t = -2,0,2下(稍微提醒一下,在Example 1中的时间轴并不是等间隔的,分别是-1,1,2),得到三组测量值b = 1,2,4。在直角坐标系中画出这三个点,这三点不在同一条直线上。如图:

用b=C+Dt表示这些点所穿过的直线,得到如下方程组:

这三个点不在同一直线上,故而无解。需要通过求解最小二乘方程组,联立正规方程。
左边:
右边:
得到:
最终得到最优解为:,
。
对应的最佳拟合直线为:
同时,求出投影向量p:
如下图所示:

现在让我们回过头来看看求解最优解的过程,在本例中,到目前为止我的计算过程和方法和前一篇文章中的Example 1中的做法一模一样,依然是直接套用和p的公式计算的,比如:
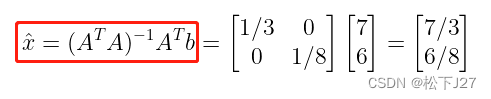
再比如:

但实际上,如果我们留心一下前面的正规方程,我们就能发现,我们可以直接通过求解正规方程,得到最优解 ,
。由于本例中矩阵A的两个列向量比较特殊,使得
是一个对角阵。这样一来,我们就可以直接写出每个方程的解。

之所以会是一个对角阵,主要原因有二:其一,向量t中所有元素的和为0,或者说测量值b1,b2和b3是在关于t=0的对称的时刻所取的值。其二,矩阵A中的两个列向量[1,1,1]和[-2,0,2]的内积为0,他们是相互正交的。
如果,实验的三个观测点所选取的三个时刻t的和不等于0,或者不关于t=0对称。(就本例而言,因为矩阵A的第一列为全1向量,因此,如果向量t的和不为0,他和另一个向量的内积就不为0)。我们可以先花点时间,通过让t减去t的均值达到,因为这样一来我们就能通过正规方程直接求出
。例如,当t=(1,3,5)时, 他的和不等于0。他的均值
, 然后让t中的每一个元素都减去均值,得到新的
=(-2,0,2)。这样一来T的和又等于0了!与此同时,直线的拟合方程也从
+
t变成了
+
T =
+
(
) =
+
(t - 3)。

这样一来,我们就不再需要通过公式去求解
和
,直接求解正规方程(Normal Equation)就能得到
和
。
事实上,这个特殊的例子和“Gram-Schmidt正交化”的思路,不谋而合。即,如果原始矩阵A中的列向量不是正交向量,则,先把矩阵A中的列向量变成正交向量。如此一来,正规方程左边的
部分就会变成一个对角阵,一旦
的结果是一个对角阵,求解
就会变的非常容易。
后面我们会看到Gram-Schmidt正交化不仅会把变成一个对角阵,不仅如此,还会把
变成一个单位矩阵,那样的话,求解方程就会变的更容易。
小结:
对于最小二乘而言,我们一开始只要求矩阵A中的各列是线性无关的,因为只有这样,才可逆。但在这里,我们不但要求A中各列线性无关,我们还要求A中的列向量是相互正交的,从而引出了Gram-Schmidt正交化的雏形。
(全文完)
作者 --- 松下J27
参考文献(鸣谢):
1,Introduction to Linear Algebra,Fifth Edition - Gilbert Strang(文中大部分插图来自于这本书)
2,绘图软件,Graphing Calculator
经典歌词赏析:
自己和自己别做扣,树和影子儿闹的啥别扭。心河打开拧了好多扣,就象开了锅的玉米粥 。
---摘自《拖网的古船没快舟》(《古船·女人和网》主题歌)

(配图与本文无关)
版权声明:文中的部分图片,文字或者其他素材,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27