(链表专题) 445. 两数相加 II ——【Leetcode每日一题】

news2024/11/16 1:50:07

445. 两数相加 II

给你两个非空链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。

你可以假设除了数字 0 之外，这两个数字都不会以零开头。

示例1：

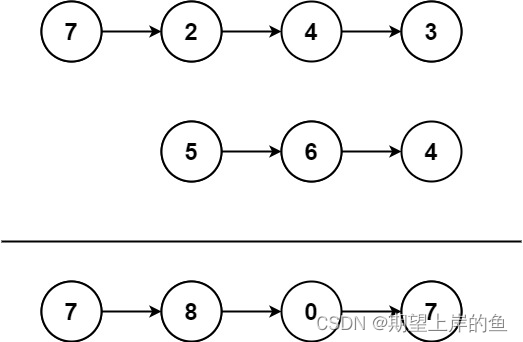
在这里插入图片描述

输入：l1 = [7,2,4,3], l2 = [5,6,4]
输出：[7,8,0,7]

示例2：

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[8,0,7]

示例3：

输入：l1 = [0], l2 = [0]
输出：[0]

提示：

链表的长度范围为 [1, 100]
0 <= node.val <= 9
输入数据保证链表代表的数字无前导 0

进阶： 如果输入链表不能翻转该如何解决？

思路：

法一：

先将两个字符串翻转，再相加；
相加结果头插法，插入新链表。

法二：进阶

链表中数位的顺序与我们做加法的顺序是相反的，为了逆序处理所有数位，我们可以使用栈：
把所有数字压入栈中，再依次取出相加。
计算过程中需要注意进位的情况。

代码：(Java、C++)

法一：
Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode tem = l1.next;
        ListNode pre = l1.next;
        l1.next = null;
        while(tem != null){//l1翻转
            tem = tem.next;
            pre.next = l1;
            l1 = pre;
            pre = tem;
        }
        tem = l2.next;
        pre = l2.next;
        l2.next = null;
        while(tem != null){//l2翻转
            tem = tem.next;
            pre.next = l2;
            l2 = pre;
            pre = tem;
        }
        tem = null;
        int carry = 0;
        while(l1 != null || l2 != null){//相加
            if(l1 != null){
                carry += l1.val;
                pre = l1;
                l1 = l1.next;
            }
            if(l2 != null){
                carry += l2.val;
                pre = l2;
                l2 = l2.next;
            }
            pre.val = carry % 10;
            carry /= 10;
            pre.next = tem;
            tem = pre;
        }
        pre = carry == 0 ? null : new ListNode(1);
        if(pre != null){
            pre.next = tem;
            tem = pre;
        }
        return tem;
    }
}

C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* tem = l1->next;
        ListNode* pre = l1->next;
        l1->next = NULL;
        while(tem != NULL){//l1翻转
            tem = tem->next;
            pre->next = l1;
            l1 = pre;
            pre = tem;
        }
        tem = l2->next;
        pre = l2->next;
        l2->next = NULL;
        while(tem != NULL){//l2翻转
            tem = tem->next;
            pre->next = l2;
            l2 = pre;
            pre = tem;
        }
        tem = NULL;
        int carry = 0;
        while(l1 != NULL || l2 != NULL){//相加
            if(l1 != NULL){
                carry += l1->val;
                pre = l1;
                l1 = l1->next;
            }
            if(l2 != NULL){
                carry += l2->val;
                pre = l2;
                l2 = l2->next;
            }
            pre->val = carry % 10;
            carry /= 10;
            pre->next = tem;
            tem = pre;
        }
        pre = carry == 0 ? NULL : new ListNode(1);
        if(pre != NULL){
            pre->next = tem;
            tem = pre;
        }
        return tem;
    }
};

法二：进阶
Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        Deque<Integer> stack1 = new ArrayDeque<Integer>();
        Deque<Integer> stack2 = new ArrayDeque<Integer>();
        while(l1 != null){
            stack1.push(l1.val);
            l1 = l1.next;
        }
        while(l2 != null){
            stack2.push(l2.val);
            l2 = l2.next;
        }
        int carry = 0;
        ListNode ans = null;
        while(!stack1.isEmpty() || !stack2.isEmpty() || carry != 0){
            carry += stack1.isEmpty() ? 0 : stack1.pop();
            carry += stack2.isEmpty() ? 0 : stack2.pop();
            ListNode tem = new ListNode(carry % 10);
            carry /= 10;
            tem.next = ans;
            ans = tem;
        }
        return ans;
    }
}

C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        stack<int> stack1, stack2;
        while(l1 != NULL){
            stack1.push(l1->val);
            l1 = l1->next;
        }
        while(l2 != NULL){
            stack2.push(l2->val);
            l2 = l2->next;
        }
        int carry = 0;
        ListNode* ans = NULL;
        while(!stack1.empty() || !stack2.empty() || carry != 0){
            carry += stack1.empty() ? 0 : stack1.top();
            carry += stack2.empty() ? 0 : stack2.top();
            if (!stack1.empty()) stack1.pop();
            if (!stack2.empty()) stack2.pop();
            ListNode* tem = new ListNode(carry % 10);
            carry /= 10;
            tem->next = ans;
            ans = tem;
        }
        return ans;
    }
};

运行结果：

在这里插入图片描述

复杂度分析：

时间复杂度： $O (ma x (m, n))$ ，其中 $m$ 和 $n$ 分别为两个链表的长度。我们需要遍历两个链表的全部位置，而处理每个位置只需要 $O (1)$ 的时间。
空间复杂度： $O (m + n)$ ，,法一为 $O (1)$ ；法二为 $O (m + n)$ ，其中 $m$ 和 $n$ 分别为两个链表的长度。空间复杂度主要取决于我们把链表内容放入栈中所用的空间。