引言
介绍了Loop, Catmull-Clark, Doo-Sabin细分。
算法介绍
1. Loop细分
Loop细分是Charles Loop在1987年在硕士论文中提出的一种对三角网格的细分算法。
Loop细分是递归定义的,每一个三角形一分为四,对于新生成的点和旧点以不同的规则更新。
点的更新规则:
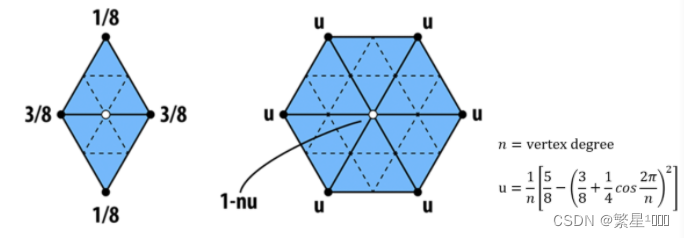
2. Catmull-Clark细分
Catmull-Clark细分是Edwin CatMull和Jin Clark在1978年提出的一种可以对任意拓扑的网格进行细分的一种算法,是递归定义的,在每一次递归中:
- 计算面点,是面的顶点的平均值
- 计算边点,是边的顶点和相邻的面点的平均值
- 计算旧的顶点,n是与点相邻的边数量, Q是相邻的面点的平均值,R是相邻的边点的平均值,v是本来的顶点
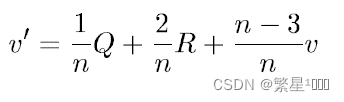
- 生成新的拓扑
3. Doo-Sabin细分
Doo-Sabin细分是Dainel Doo和Malcolm Sabin在1978年提出的一种可以对任意拓扑的网格进行细分的一种算法,是递归定义的,在每一次递归中:
-
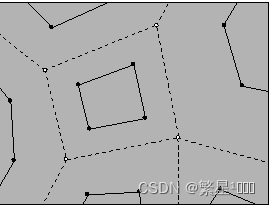
计算面的中心点和边的中心点,对于每一个点P,计算一个新的点P’, 是点,相邻的边的中心点和面的中心点的平均值。
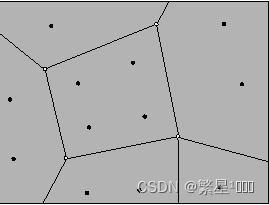
-
对于每一个面,连接面内的新点生成新的面
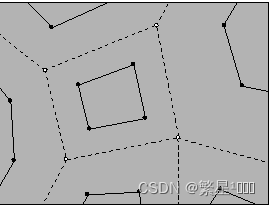
-
对于每一个点,连接点周围的新点生成新的面
-
对于每一条边,连接边相邻的新点生成新的面
参考资料
[1] Mesh-Subdivision(Github)
[2] loop曲面细分算法c++实现 https://blog.csdn.net/suian0424/article/details/86371383
[3] Doo-sabin曲面 http://graphics.cs.ucdavis.edu/education/CAGDNotes/Doo-Sabin/Doo-Sabin.html
[4] 细分曲面Catmull-Clark Subdivision算法 https://blog.csdn.net/tspatial_thunder/article/details/5938771






![[acwing周赛复盘] 第 94 场周赛20230311](https://img-blog.csdnimg.cn/4803447c73444805a85425e045de926f.png)