最近做到一道好题，特来和大家分享一下。

news2024/10/5 21:13:37

题目：299. 裁剪序列 - AcWing题库
分析：
题目给我们的数据范围是10⁵;也就是说我们的时间复杂度要控制到O(nlog₂n)才可以。假设每一个元素都可以作为一个区间，那么可以有

C_n¹+……+C_nⁿ= 2ⁿ-1种划分方法，n达到了10⁵,很显然就超时。所以暴力枚举绝对会超时。所以我们需要优化。

优化主要采用DP或者贪心。可以先考虑DP，如果答案都是f[i]的一个子集里，那么我们就可以使用贪心。

DP我们这里采用闫氏DP分析法：
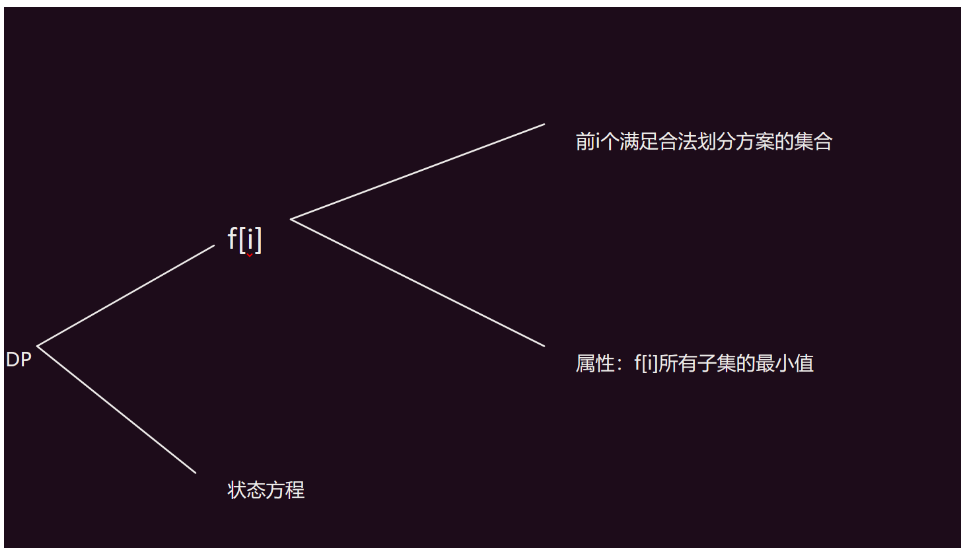
在这里插入图片描述
那f[i]集合如何划分？

每一次加入第i位置的元素，会对整体造成什么影响呢？---->最后一段的长度发生变化，那么最后一段的最大值也可能发生变化。或者说，因为i的加入，可能导致原来最后一段加上当前i位置的值大于m。这样就需要重新划分。所以说最后一段长度我们可以设为k：

在这里插入图片描述
对于不同的k，都会产生不同的结果。因此我们对于f[i]的子集划分就有了依据：

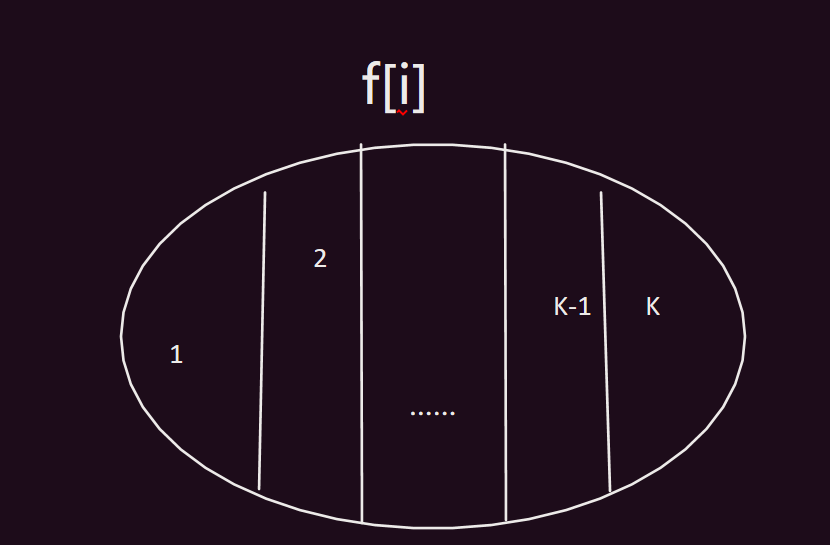
状态方程如何计算？最后一段选了长度为k的，最大值为a_max，那么前面就是f[i - k].所以说最后的状态方程就是:
$f[i] = min(f[i], f[i - k] + a_{max})$
我们再仔细的分析，发现我们循环i的时候，每次都要循环k，并且我们还需要在这k里找出来每种方案的最小值还是一层遍历，因此时间复杂度会达到O(n³)级别，还是会超时。当然我们在求每一种方案的最小值的时候，我们在循环k的时候设一个变量来保存最后一段为k的最小值，这样我们的时间复杂度就降到了O(n²).

因此我们还需要进行优化：

最后一段的长度是有限制的，区间内元素的和不能大于m。假设最后一段的长度达到最大，我们使用j来表示最后一段区间最左边的点，（如果是j-1,那么我们最后一段的和就要大于m）：
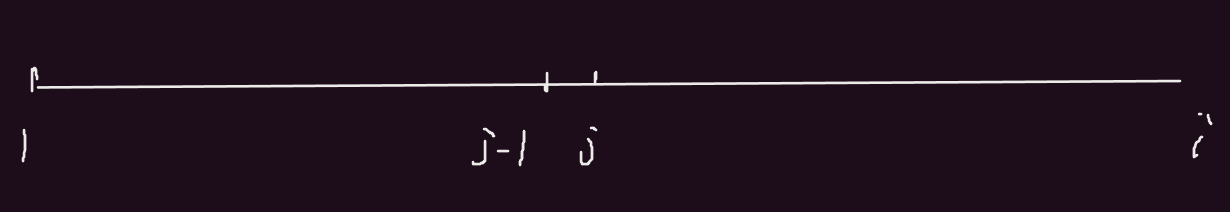
在这里插入图片描述
当最后一段的长度达到最大值，最后一段左边最远的位置就是j，那么前面j-1的最小值就是f[j - 1].

对于当前的[j , i]，区间内有最大值a_max1如图：
在这里插入图片描述
当前的区间最大值就是a_max1,那么这种划分的方案的结果为f[j - 1] + a_max1.我们再看j的位置，如果j取到(j, k₁]这个范围内j^’，首先最后一段的最大值是不会发生改变还是a_max1。变化的是f[j^’ - 1].所以我们目前需要分析f[j^’ - 1]的变化。
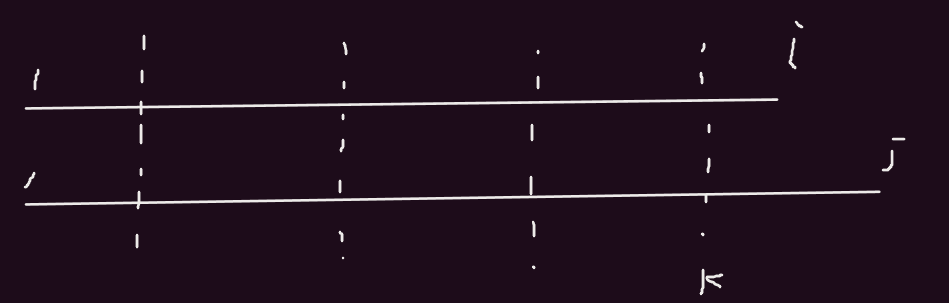
在这里插入图片描述
f[j] ≥ f[i].对于这两段，首先可以是可以找到位置k，这两段的f[k]都是相等的。剩下的不就是最后一段的比较.题目里说元素都是非负数,所以(i, j]里的数与原来i的最后一段合并，最大值还是i区间里的最后一段的最大值；也可能使得元素之后大于m，在(i, j]里有产生了新的段，这一段的最大值也得是一个非负数，所以我们可以得到f[j] ≥ f[i].

好，我们现在回到这里：
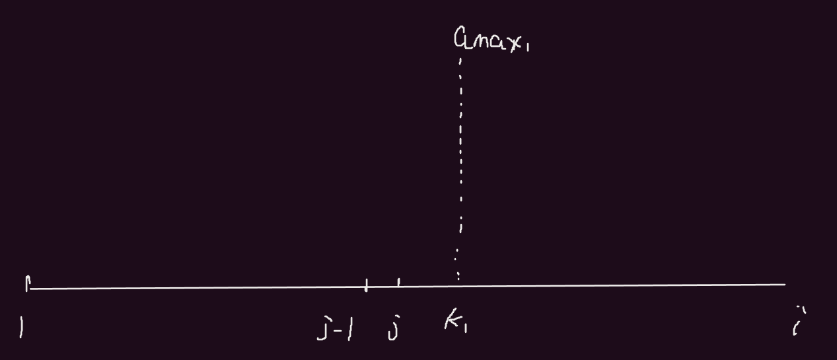
在这里插入图片描述
这里j是最左边的位置，如果j^’在[j, k₁]的范围内，最大值都是a_max，而变化的就是f[j^’ - 1].j^’是不断变大的，但是我们要记住我们是求最后一段所有方案最大值中的最小值.所以这里我们贪心一下,j^’∈[j, k₁]的时候f[j^’ - 1] _min = f[ j - 1].所以我们不需要枚举这一段里的j只需要有j即可。

那如果说j > k₁呢？
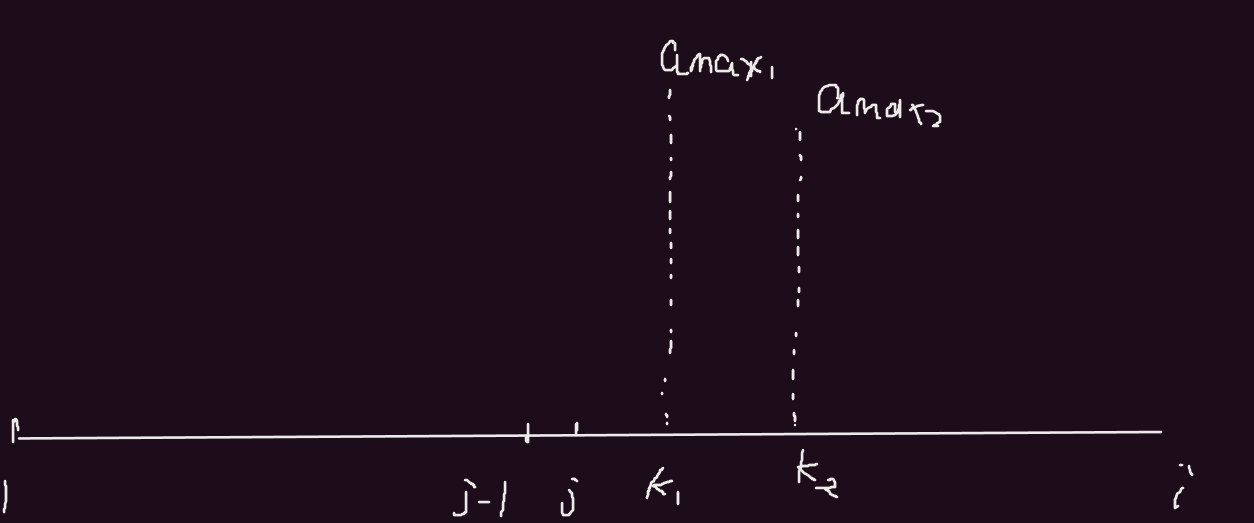
在这里插入图片描述
j∈(k₁, k₂]的时候，那么最后一段区间的最大值就是a_max2。利用我们上面分析a_max1的结论，我们可以很容易得到：如果j∈(k₁, k₂]，那么当前方案的最小值是f[k₁] + a_max2 (j的位置在k₁ + 1处。)

所以我们依次推导：
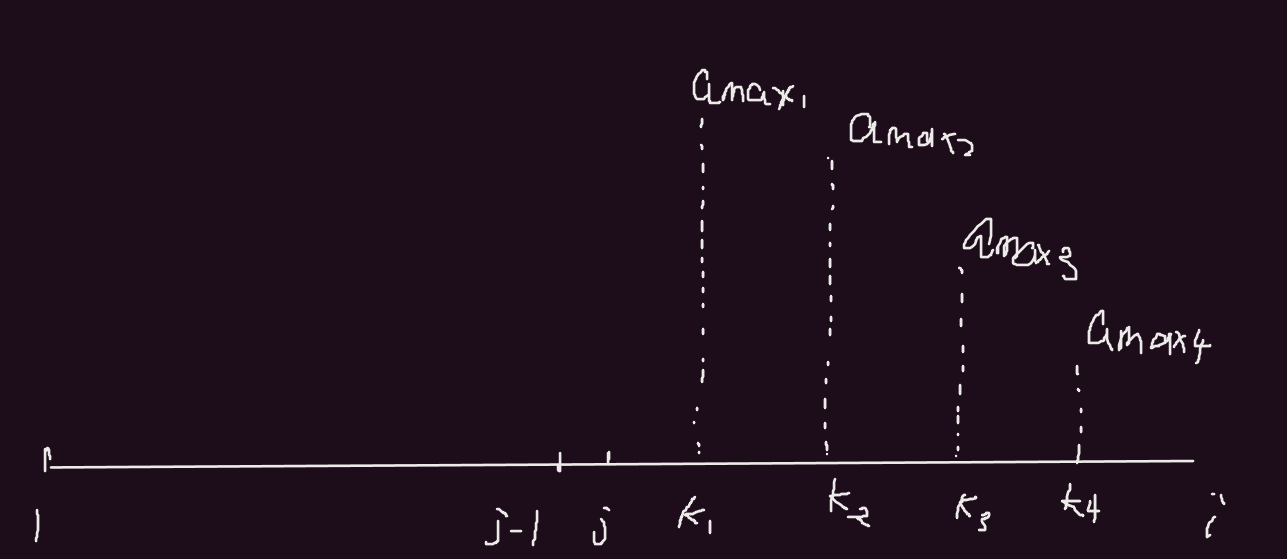
在这里插入图片描述
我们发现最后一段我们只需要维护一如上图所示的单调队列即可。在这个单调队列里面，如果加入一个i，就需要将i加入队列即可。如果加入的i的值≥a_max4，那么就把a_max4的值弹出。就这样依次进行下去直到当前i的值 < 当前队尾的元素，这样就把当前i的值加入到队尾。

对于队头，我们还需要检查当前每次加入一个i的时候，当前队列的元素是不是大于m，如果大于m，j就需要往右移（也就是抛去队头）

对于每一段我们只需要取队头元素即可，因为队头元素是最后一段里最大的值。但是我们不要忘记了，我们要取的是最后一段所有方案的最大值中的最小值。也就是说我们还需要循环这样一个队列找到其中的最小值（f[j -1] + a_max）。因为我们的时间复杂度还可能是O(n²)的。

因此我们需要维护一个集合，这个集合可以动态地增加一个数（队尾插入），删除一个数（队头删除），并且求最小值（f[j -1] + a_max）

我们可以使用堆来维护这样的一个集合，堆可以动态的增加一个数，删除一个数，并且求最小值，而且时间复杂度是O(log₂n)的。这里堆只能删除头结点，不能删除任意的节点。(这里为什么不能用目前还未知，这个问题就先留着)

所以这里可以使用平衡树，可以动态的增加一个数，删除一个数，并且求最小值，时间复杂度都是O(log₂n).

C++里可以使用set。这一题里集合里可能会出现相同的值，因此我们这里使用

ok!完美！时间复杂度成功降到题目要求的范围！

#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>

using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL f[N], m;
int n;
int w[N], q[N];
multiset<LL> S;
void remove(LL x)
{
    /*
    * 因为不同的节点可能会存储相同的值，因此这里只需要删除一个值就行
    * 使用S.erase(x);会删除所有等于x的元素。
    */
    auto it = S.find(x);
    S.erase(it);
}
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
    {
        cin >> w[i];
        // 如果当前的元素>m那么这个元素可能不能属于任何一个组，那么就报错，就是-1
        if(w[i] > m)
        {
            cout << "-1" << endl;
            return 0;
        }
    }
    int hh = 0, tt = -1;
    LL sum = 0;
    for(int i = 1, j = 1; i <= n; i++)
    {
        sum += w[i];
        while(sum > m)
        {
            // 找当前最后一个区间的j的最小值。
            sum -= w[j++];
            if(hh <= tt && q[hh] < j) // 删除队头
            {
                // 只在队列中的相邻两个位置之间选择，如果只有一个元素，那么就直接加入multiset集合里就行
                // 这里的if做的就是删除队头的任务
                if(hh < tt) remove(f[q[hh]] + w[q[hh + 1]]);
                hh++;
            }
        }
        
        // 往队尾插入元素
        while (hh <= tt && w[q[tt]] <= w[i] )
        {
            // 删除一个队尾的元素，其实也得删除它在集合multiset中对应的元素。
            if(hh < tt) remove(f[q[tt - 1]] + w[q[tt]]);
            tt--;
        }
        q[++tt] = i; //将当前的位置加入到队列里
        if(hh < tt) S.insert(f[q[tt - 1]] + w[q[tt]]);// 如果当前队列的元素数量大于1，那么就把当前队列的对应的值插入集合当中
        
        f[i] = f[j - 1] + w[q[hh]]; // 这里其实也就是处理了队列里只有一个元素的情况，结果就是最后一段的前一个地址的f[j - 1]加上当前队头的值
        if(S.size()) f[i] = min(f[i], *S.begin()); // *S.begin()就是取到集合中的最小值，其实也就是当前f[i]所有方案的最小值
    }
    cout << f[n] << endl;
    return 0;
}