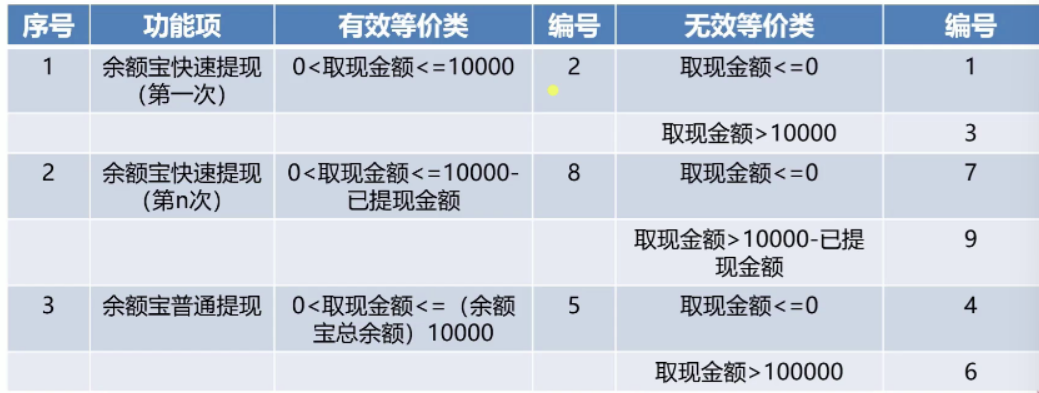
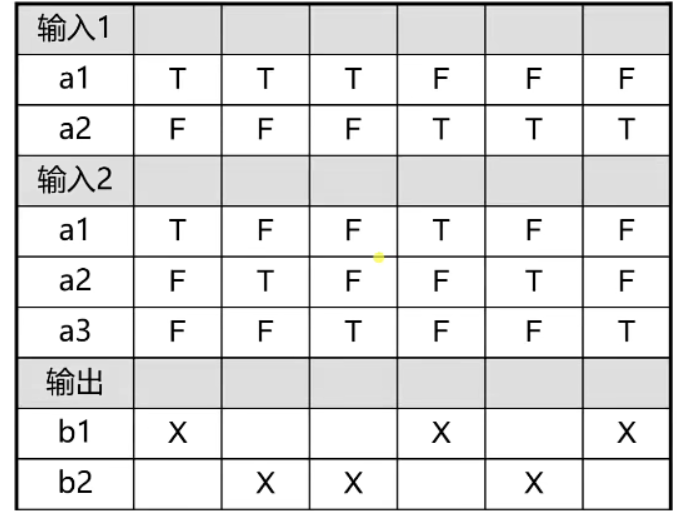
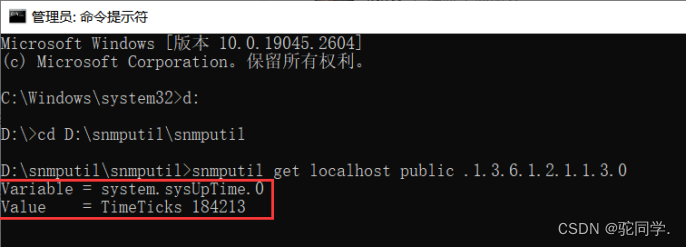
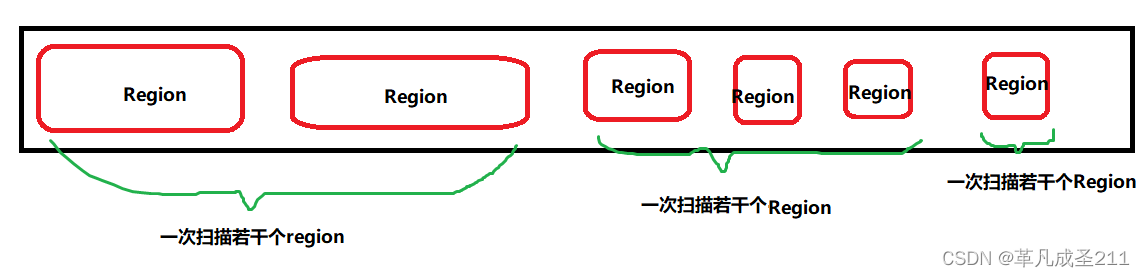
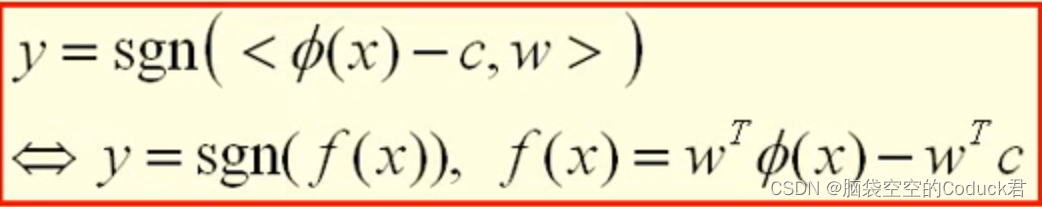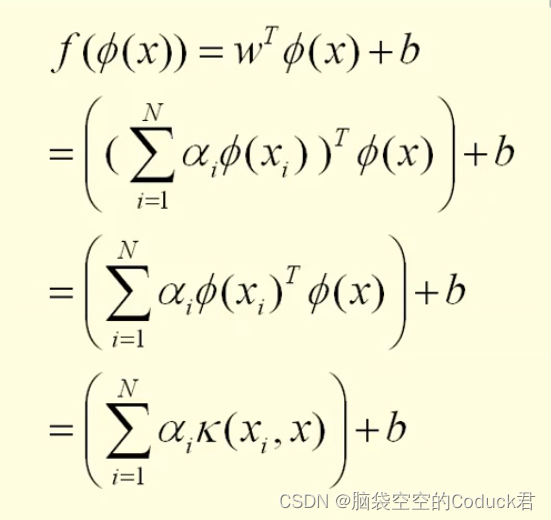核方法
核方法定义
一种能够将在原始数据空间中的非线性数据映射到高维线性可分的方法。
核方法的用处
1、低维数据非线性,当其映射到高维空间(feature space)时,可以用线性方法对数据进行处理。
2、线性学习器相对于非线性学习器有更好的过拟合控制从而可以更好地保证泛化性能,同时,利用核函数将非线性映射隐含在线性学习器中进行同步计算,使得计算复杂度与高维特征空间的维数无关。
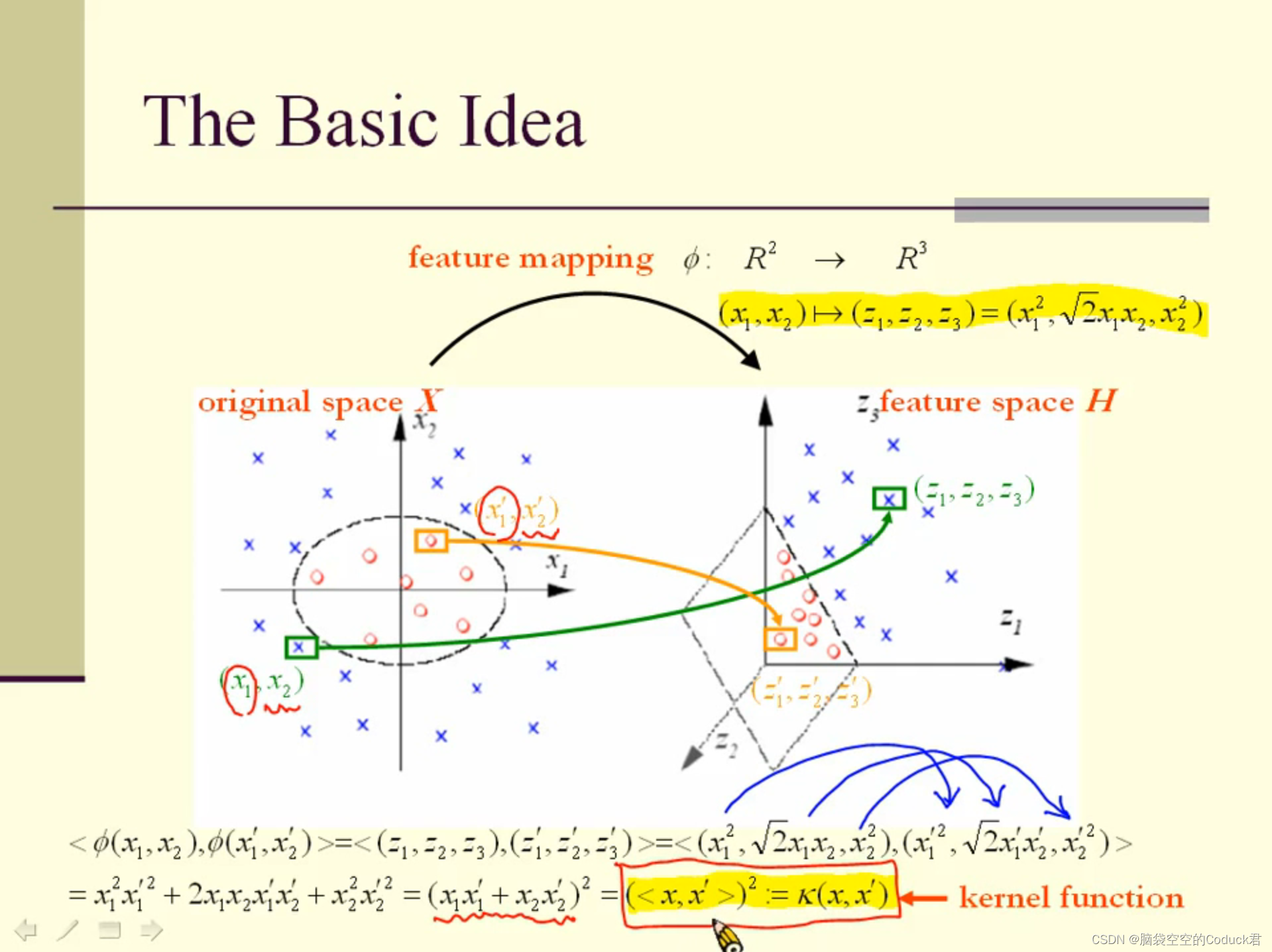
如上,是将二维空间的非线性数据通过
ϕ
\phi
ϕ,把数据映射到了三维空间中。
并且我们发现,在高维空间中两个数据的内积,是原空间中对应数据的函数
(如上的
<
ϕ
(
x
1
,
x
2
)
>
,
<
ϕ
(
x
1
′
,
x
2
′
)
>
=
(
<
x
,
x
′
>
)
2
<\phi(x_1,x_2)>,<\phi(x_1',x_2')>=(<x,x'>)^{2}
<ϕ(x1,x2)>,<ϕ(x1′,x2′)>=(<x,x′>)2),该函数被定义为
K
(
x
,
x
′
)
K(x,x')
K(x,x′),称为核函数(将原始空间中的向量作为输入向量,并返回特征空间(转换后的数据空间,可能是高维)中向量的点积的函数称为核函数)。
注意:将数据映射到不同的高维空间,其对应的核函数不同。
核函数作用
1、通过
K
(
x
,
x
′
)
K(x,x')
K(x,x′)我们可以直接计算出在feature space(高维空间)中点的两点间的距离平方和两个向量间的角度。

2、由于可以通过1中的方法计算出高维空间的距离和角度,我们完全可以不去计算出
ϕ
\phi
ϕ(一般
ϕ
\phi
ϕ难计算),可由
K
(
x
,
x
′
)
K(x,x')
K(x,x′)直接处理高维空间的数据。
3、避免在高维空间运作,选择一个特征空间,其中点积可以使用输入空间中的非线性函数直接求值,降低了计算的复杂度(在高维空间中考虑的维数过多,计算也相当复杂)。
核矩阵
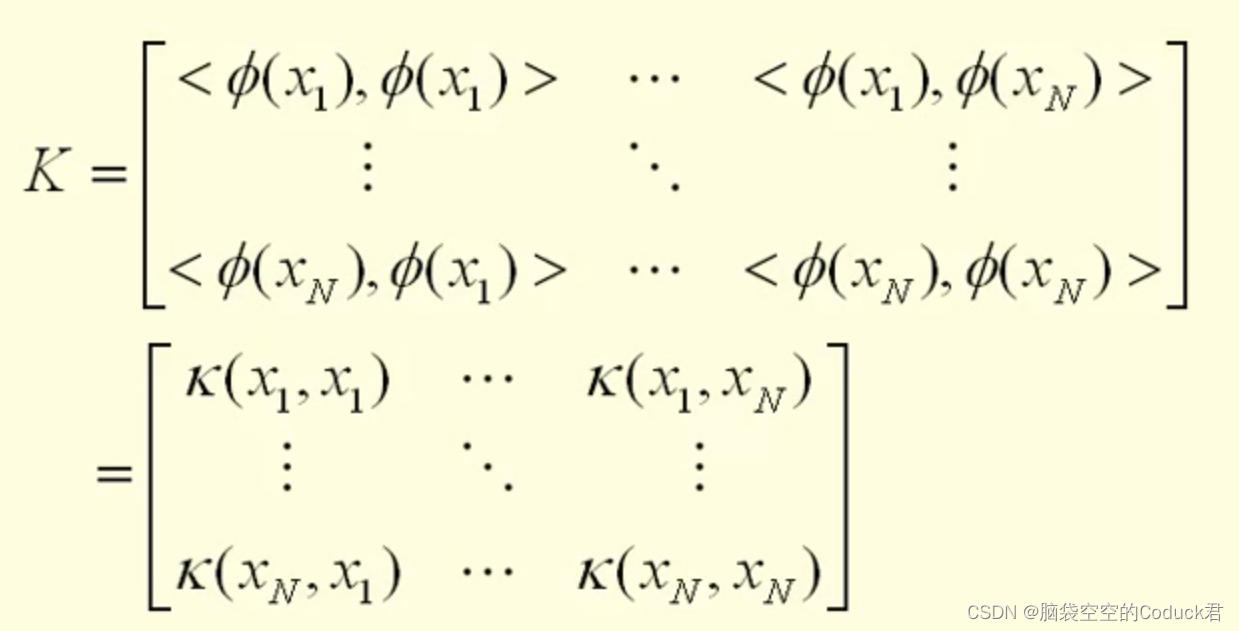
核函数要满足的条件
有限正半定(给定任意有限 n个点(x1~xn),求解其矩阵是正定的)
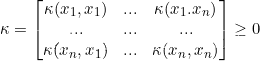
常用核函数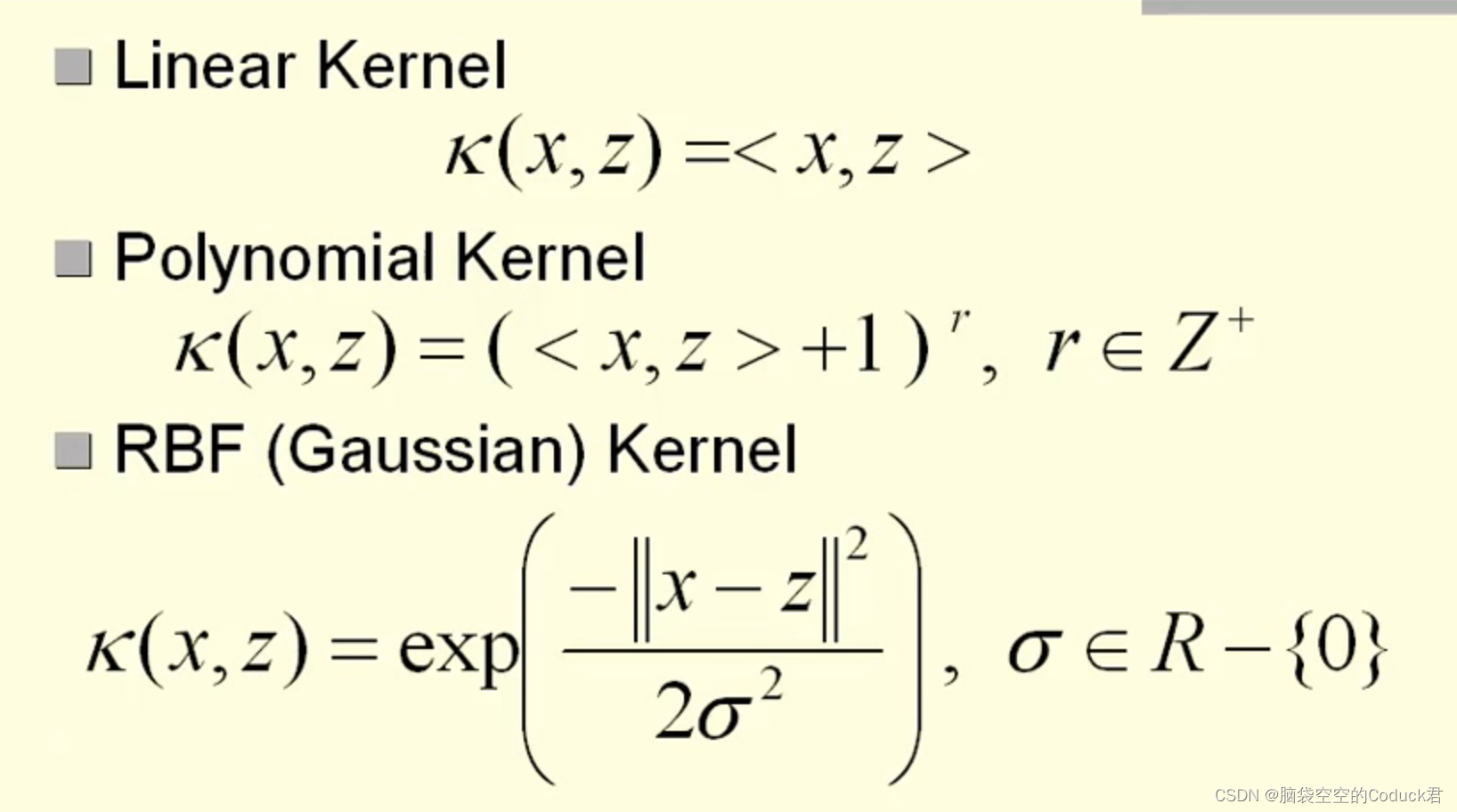
K ( x , x i ) K(x,x_i) K(x,xi)与 ϕ \phi ϕ的关系
●只要知道kernel function,φ就不是必须的
●只要知道kernel function就可以达到计算需求
●有限半正定的kernel matrix可以使用
●k和φ是一一对应的
●知道kernel function 可以构建feature space
简单例子
y i y_i yi是标签,只有两个类别+1和-1,然后利用φ将x映射到更高维空间φ ( x ),下面就是投影之后的空间。同时计算出不同类别数据的两个中心点
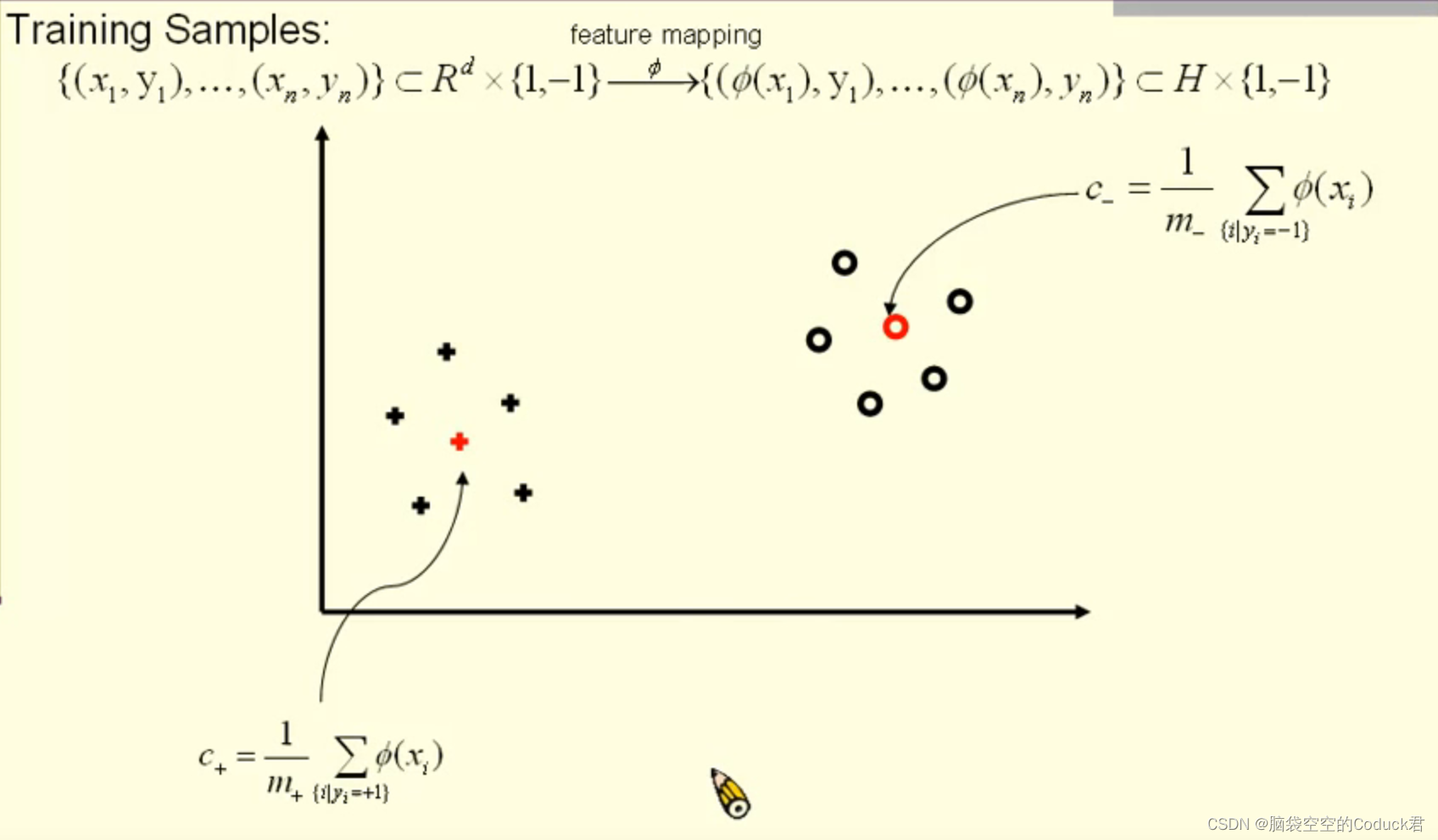
然后计算出中垂线,通过新数据向量
ϕ
(
x
)
\phi(x)
ϕ(x)与向量w的所成角来判断新数据的类别
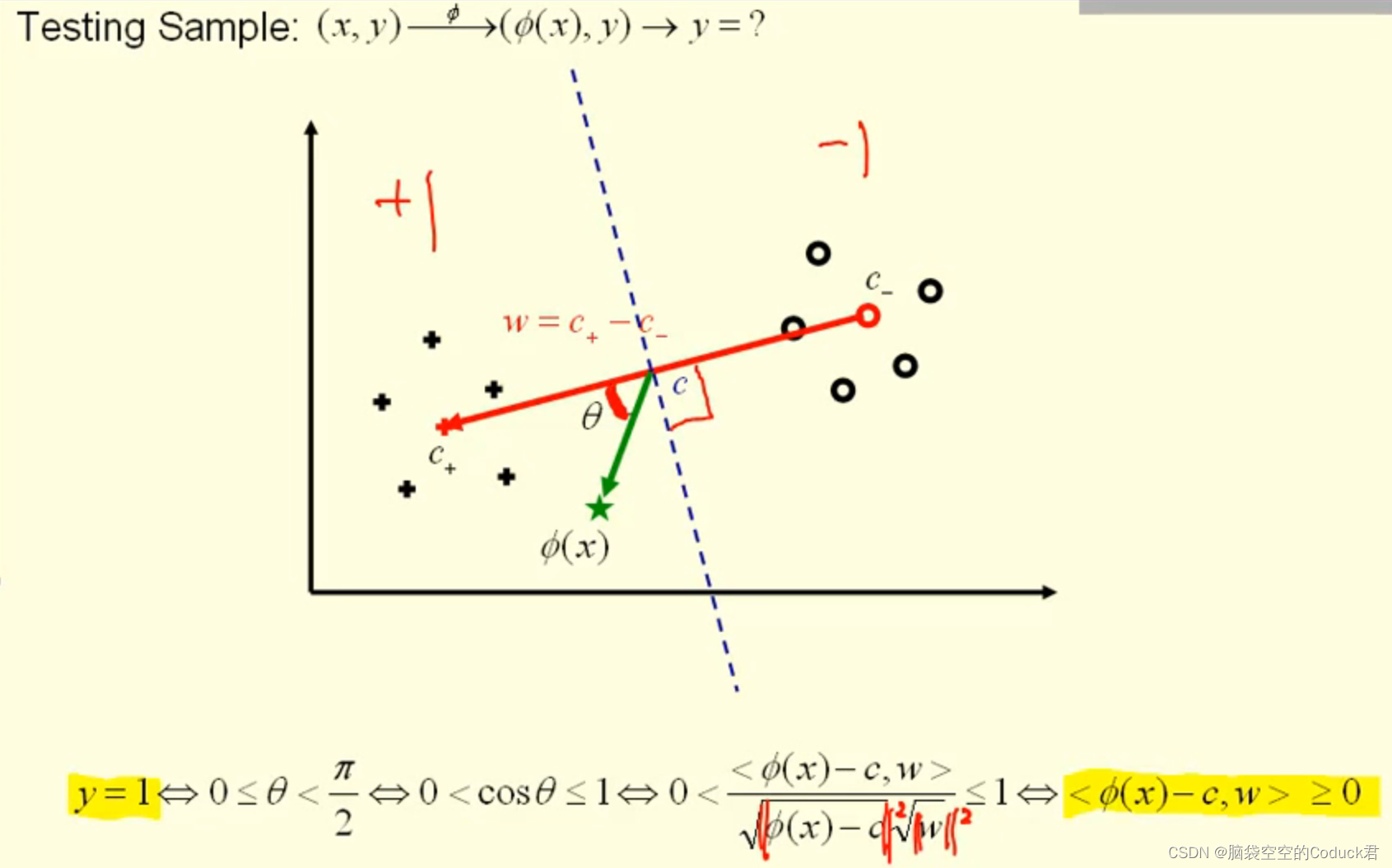
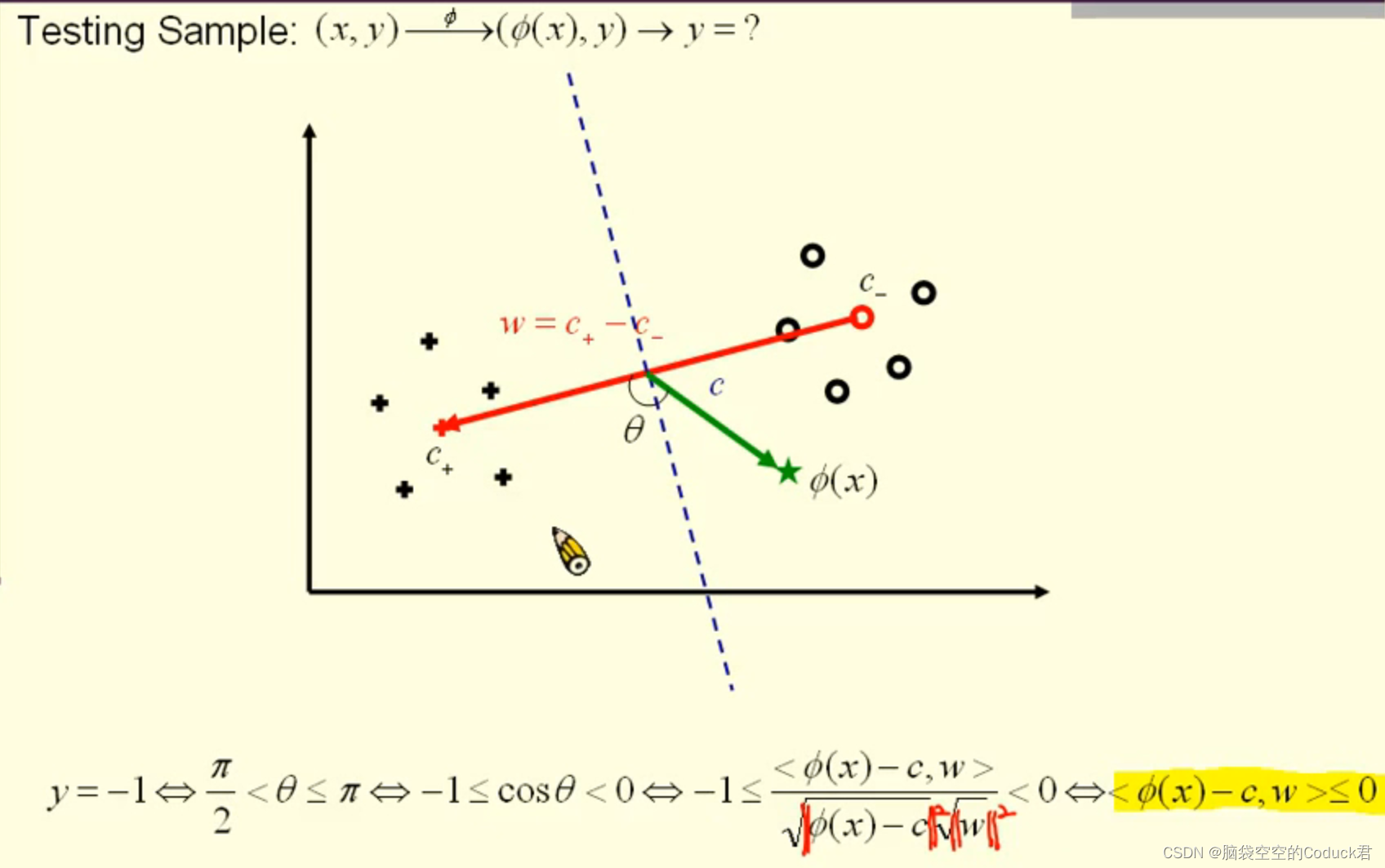
由上面知,可以通过sign函数来判断新数据类别
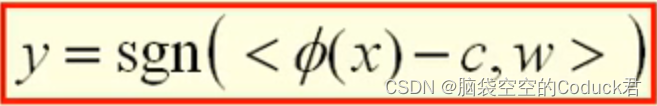
以下是
<
ϕ
(
x
)
−
c
,
w
>
<\phi(x)-c,w>
<ϕ(x)−c,w>的计算方法,同样是可以用核函数来表示

Dual Representation
我们还可以用线性表达式来表示上面的式子