2023年中国高校计算机大赛-团队程序设计天梯赛（GPLT）上海理工大学校内选拔赛（同步赛)

A – A Xor B Problem

题目分析

只有相同数字异或结果才为零，统计一下相同数字出现的次数，排列组合即可。

根据样例来看，自身与自身是可以成为一对数字的。

code

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int N = 1010;

int n, m, k, t;
int a[N];
map<int, int>q;

signed main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++)
    {
        cin >> a[i];
        q[a[i]] ++;
    }

    int ans = 0;
   for(auto &[k, v] : q)
   {
       if(v >= 2) ans += v * v;
       else ans ++;
   }

    cout << ans << "\n";;

    return 0;
}

B – 吃苹果

题目分析

可以通过按照早上和晚上吃苹果愉悦值得差值来排序，差值越大得越优先被处理贡献值越大。

code

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int N = 1e5 + 10;

int n, m, k, t;
bool st[N];

struct node
{
    int l, r;
}q[N];

bool cmp(node a, node b)
{
   return abs(a.l - a.r) > abs(b.l - b.r);
}

signed main()
{
    cin >> n >> k;
    for(int i = 1; i <= n; i ++)
    {
        int u, v;
        cin >> u >> v;
        q[i] = {u, v};
    }

    sort(q + 1, q + n + 1, cmp);

    int ans = 0;
    int r1 = n - k, r2 = k;
    for(int i = 1; i <= n; i ++)
    {
        if(q[i].l > q[i].r)
        {
            if(r1)
            {
                ans += q[i].l;
                r1 --;
            }
            else ans += q[i].r, r2 --;
        }
        else
        {
            if(r2)
            {
                ans += q[i].r;
                r2 --;
            }
            else ans += q[i].l, r1 --;
        }
    }

    cout << ans << "\n";

    return 0;
}

C – n皇后问题

题目分析

每输入一个点判断其八个方向上是否已经被放过即可，不过判断时暴力手法得判断会超时，我们可以通过判断是否在一条直线上的方式来判断会不会冲突。

横向和纵向的比较简单，问题是处理两个对角线。两个对角线为y=x+a和y=-x+b，可以通过x和y来看常数是否相同从而判断是否在一条直线上。

code

#include<bits/stdc++.h>
using namespace std;

const int N = 1e7 + 10;

int n, m, k, t;

bool row[N], col[N], dg[N], udg[N];

bool get(int x, int y)
{
    if(!row[x] && !col[y] && !dg[x + y] && !udg[n - x  + y])
    {
        row[x] = col[y] = dg[x + y] = udg[n - x + y] = true;
        return true;
    }

    return false;
}

signed main()
{
    scanf("%d%d", &n, &t);

    while(t --)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        if (get(x, y)) puts("Yes");
        else puts("No");
    }

    return 0;
}

D – 分苹果

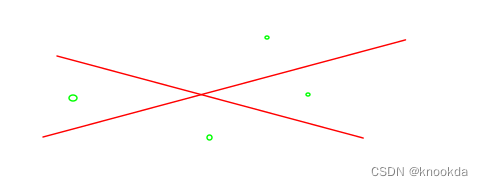
题目分析

可以看作两个木棒把一个桌面分成了四个部分，带入点坐标根据数值得结果可以判断在哪个部分。

code

#include <bits/stdc++.h>
#define int long long

using namespace std;

int a[5];
int n, m, k, t;
int Ae, Be, Ce;
int Ar, Br, Cr;

signed main()
{
    cin >> n;
    cin >> Ae >> Be >> Ce;
    cin >> Ar >> Br >> Cr;

    for(int i = 1; i <= n; i ++)
    {
        int x, y;
        cin >> x >> y;

        int ans1 = Ae * x + Be * y + Ce;
        int ans2 = Ar * x + Br * y + Cr;

        if(ans1 > 0 && ans2 > 0) a[1]++;
        else if(ans1 > 0 && ans2 < 0) a[2]++;
        else if(ans1 < 0 && ans2 > 0) a[3] ++;
        else if(ans1 < 0 && ans2 < 0) a[4] ++;
    }

    sort(a + 1, a + 5);
    for(int i = 1; i <= 4; i ++) cout << a[i] << " " ;
}

E – 完型填空

题目分析

本体数据范围较小并且分成的情况很多，可以采用动态规划的方法。

集合f[i][j][k][r]表示：A选项选了i个，B选项选了j个，C选项选了k个，D选项选了f个，所得期望的值的集合

根据思考前一个得方法，可以很容易得到状态转移方程。

code

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int N = 110;

int n, m, k, t;
int a[N], w[N][5];
int f[N][N][N][N];

signed main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= 4; j ++)
            cin >> w[i][j];

    n /= 4;
    for(int i = 0; i <= n; i ++)
        for(int j = 0; j <= n; j ++)
            for(int k = 0; k <= n; k ++)
                for(int r = 0; r <= n; r ++)
                {
                    if(i > 0)
                        f[i][j][k][r] = max(f[i][j][k][r], f[i - 1][j][k][r] + w[i + j + k + r][1]);
                     if(j > 0)
                        f[i][j][k][r] = max(f[i][j][k][r], f[i][j - 1][k][r] + w[i + j + k + r][2]);
                     if(k > 0)
                        f[i][j][k][r] = max(f[i][j][k][r], f[i][j][k - 1][r] + w[i + j + k + r][3]);
                     if(r > 0)
                        f[i][j][k][r] = max(f[i][j][k][r], f[i][j][k][r - 1] + w[i + j + k + r][4]);
                }

    cout << f[n][n][n][n] << "\n";

    return 0;
}