【C++】图

news2024/10/7 20:27:33

本文包含了图的基本概念

1.相关概念

1.1 无/有向

无向图：每一个顶点之间的连线没有方向

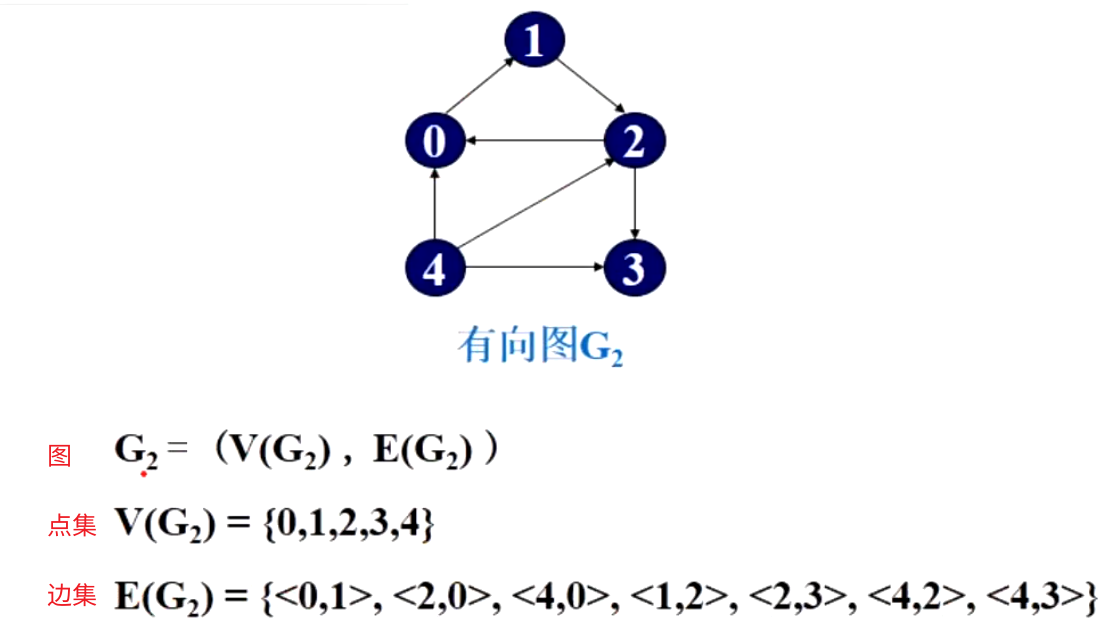
有向图：连线有方向（类似离散数学的二元关系 <A,B>代表从A到B的边，有方向）

<A,B>中A为始点，B为终点

在无向图中，(V,U)和(U,V)是同一条边

1.2 顶点和边

图中的节点叫做顶点。

顶点之间的线条就是边，表示事物与事物之间的关系。

image-20221203152531855

1.3 自回路/多重图

image-20221203152631926

1.4 完全图

图中每一个顶点都有连线（有最多的边数）就叫做完全图

设顶点为N个

  • 无向完全图中n(n-1)/2条边
  • 有向完全图中n(n-1)条边

1.5 邻接与关联

无向图中(u,v)是一条边

  • 顶点u和v邻接
  • 边(u,v)与顶点u和v相关联

1.6 子图

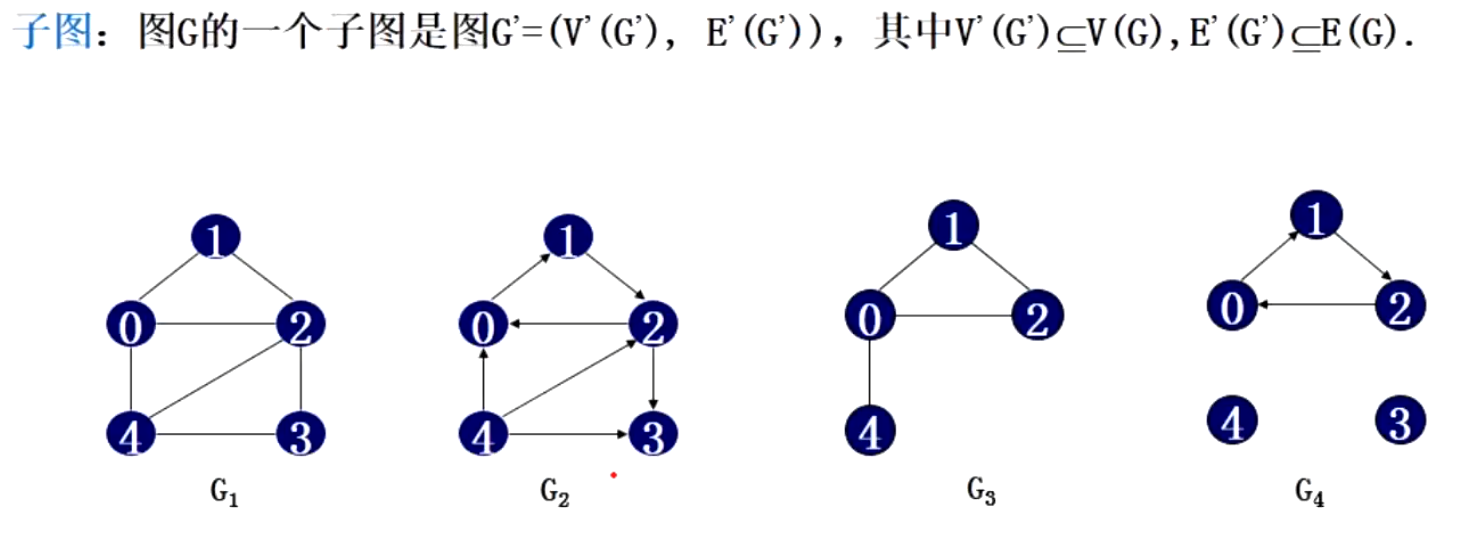
image-20221203153003325

图中G3是G1的子图，G4是G2的子图

简单说来，就是子图是原图的一部分，包括顶点、边（注意方向）都是原图中的一部分

1.6 路径

路径是顶点序列

路径是一个节点到另外一个节点需要经过的边

  • 路径长度：路径上边的数目
  • 简单路径：除起点、终点可以相同外，路径中其余顶点不相同
  • 回路：起点和重点相同的简单路径

1.7 连通图

两个顶点之间只要有路径，那就是连通的

  • 连通图：无向图中任意两点之间都有路径，那么就是一个连通图
  • 连通分量：无向图的极大连通子图

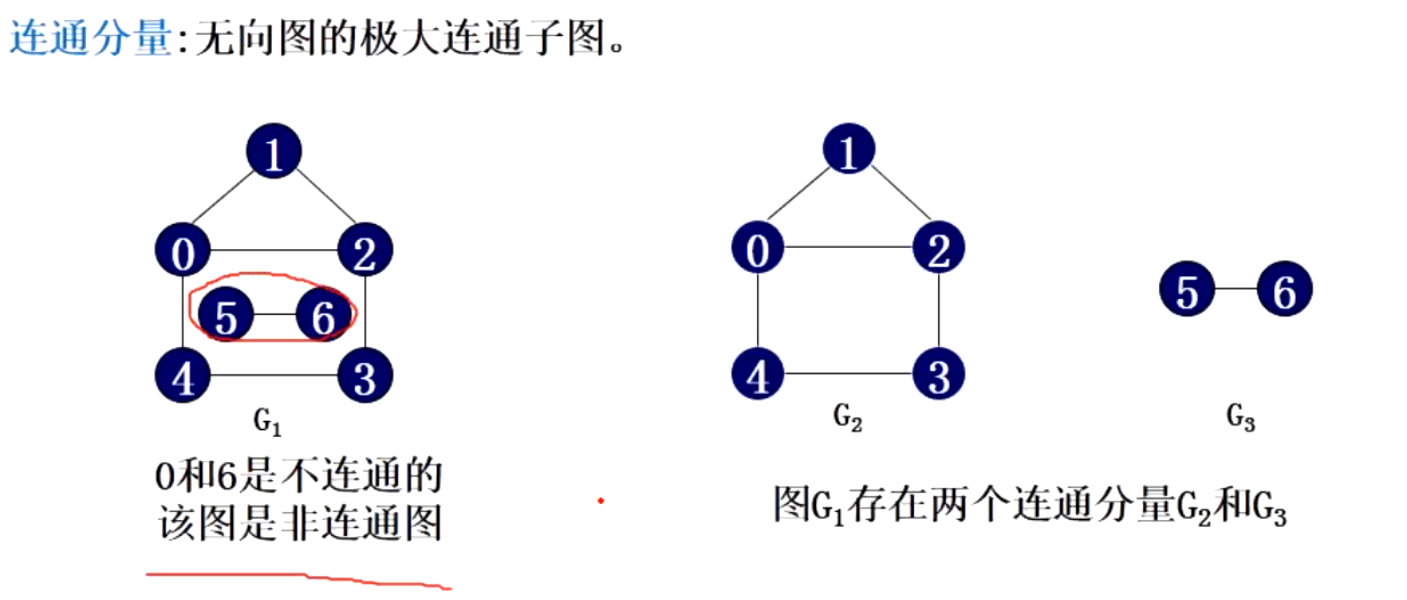
image-20221203153649688

注意，虽然连通分量被称为“极大连通子图”，但它并不是节点最多的哪一个。比如上图中的G2和G3都是极大连通子图。

  • 强连通图：有向图中，如果两个顶点之间U和V之间有U到V的路径，那就一定有从V到U的路径
  • 强连通分量：有向图的极大联通子图

image-20221203154021923

强连通图G1的极大强连通分量就是它自己（只有非强连通图才有多个强连通分量）

上图中G2就不是强联通图，因为4节点没有入边（也就没有节点能到4）

  • 第三图的上半部分并非G1的强连通分量，但是是G2的强力连通分量。
  • 同时，单独的4顶点也是一个强连通分量（单独顶点都是）

1.7 顶点的度

度：与该顶点相关联的边的数目

  • 入度：射入v的边的数目
  • 出度：从v射出去的边的数目

1.8 生成树

生成树包含图中的所有顶点，但是只有足够构成一颗树的n-1条边

  • 因为n-1条边再加上一条就会构成回路
  • 生成树中不包含回路

1.9 网

给图中的每条边都添加上权值，带权的图称为网

2.表示法

2.1 邻接矩阵

用二维数组来表示每个顶点之间的关系（矩阵）

image-20221203162700284

优缺点

优点

  • 便于判断两个顶点之间是否有边，可以直接根据下标判断，O(1)
  • 便于计算各个顶点的度
    • 无向图：第i行元素之和就是顶点i的度（前提是用1来表示）
    • 有向图：第i行元素之和为顶点i的出度；第i列为入度

缺点

  • 如果节点多，边少，就会出现空间浪费
  • 无法方便地找到一个顶点和那一条边相连（需要遍历）
  • 对于无向图，也会出现空间浪费

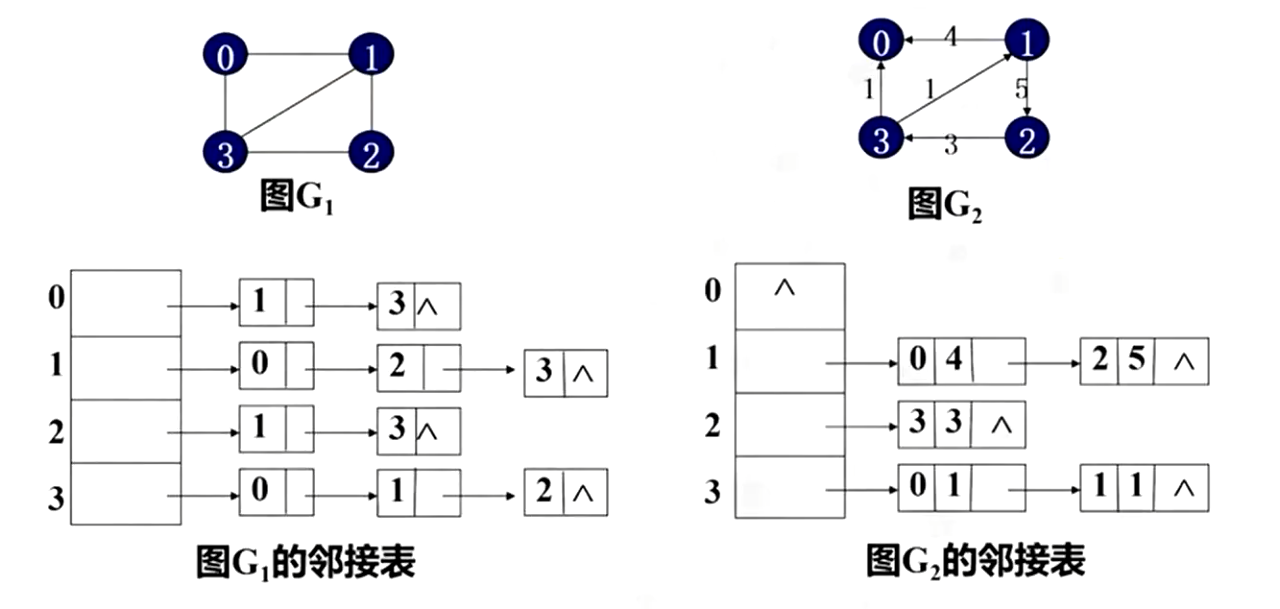
2.2 邻接表

邻接表有些类似于哈希表的拉链法。每一个节点后面跟着一个单链表，用于存储与这个节点相连的节点。

在G2的有向图中，一般存储的是出度表，即从该节点出发的边。如果边有权值，则还需要存储权值

image-20221204134044713

优缺点

优点：

  • 可以快速找到一个节点和谁相连（出度）

缺点

  • 不便于判断两个顶点之间是否有边
  • 不便于计算有向图各个顶点的度（需要遍历所有节点）

关于第二个缺点，可以新增一个入度表（即一个出度表/一个入读表）来计算。但是这样会增加时空复杂度。

3.遍历

3.1 深度优先DFS

深度优先以递归为基本思路，从一个结点开始，递归向后遍历这个节点的单链表中的节点。

image-20221204134842519

为了避免同一个节点遍历多次，我们需要有一个bool数组来标识一个节点是否遍历过。如果遍历过，则把对应下标的值设定为true来标识

由于深度优先的递归部分只能遍历连通图。若出现了上图中非联通的情况，需要我们在外循环中重新遍历一下bool标识数组，确认所有节点都遍历完成。

如果漏了节点（就是没有和其他节点联通的独立节点）那么就以此节点开头再进行一次深度遍历。

image-20221204140840949

3.2 广度优先BFS

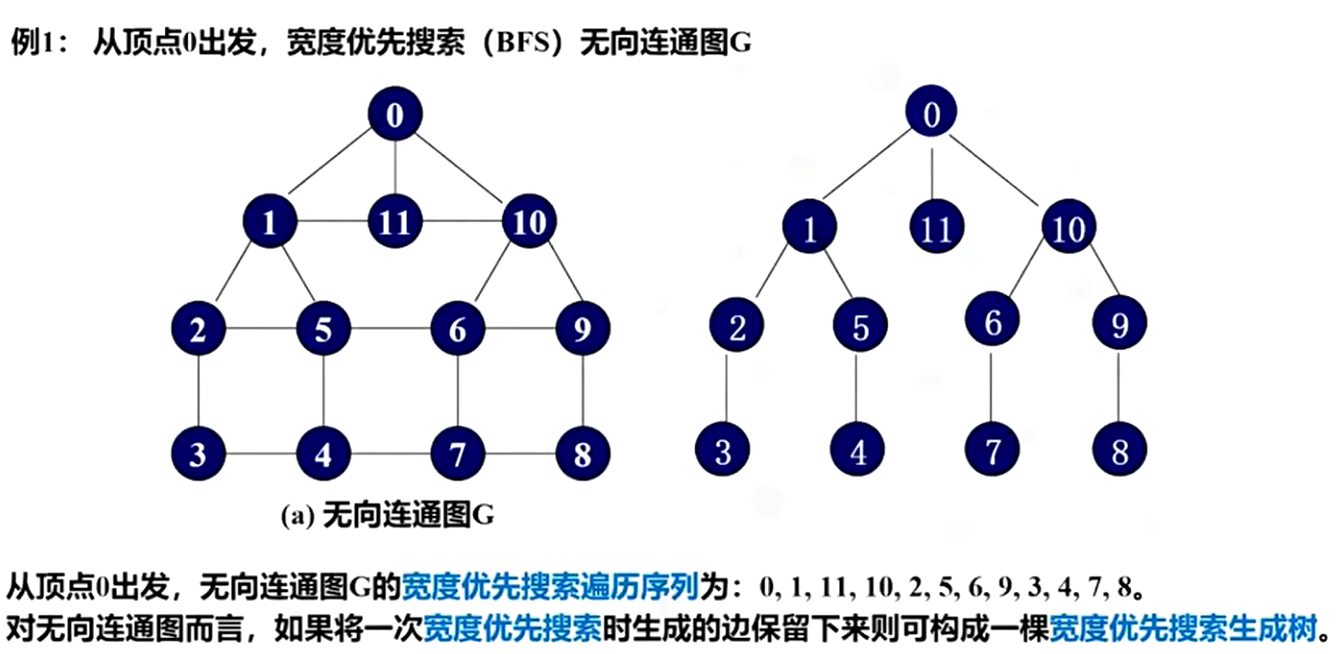
image-20221204140627539

广度优先遍历类似二叉树的层序遍历，依靠循环+队列来完成遍历

  • 入起始节点，打印起始节点的值
  • 出队头节点（第一次的时候是起始节点）往队列中入该节点单链表中的所有节点
  • 依此类推，出一个节点，就入这个节点单链表中的所有节点
  • 同样地用一个bool数组标识节点是否被访问。如果被访问了则跳过该节点
  • 也需要在队列循环结束后遍历一遍bool数组，确认所有节点都访问完毕。

image-20221204140819112

3.3 判断一个图是否连通

使用任何遍历方式，遍历完毕后检查bool数组

若有节点没有被访问，则说明是非连通图

4.拓扑排序

https://blog.csdn.net/qq_43448856/article/details/119959241

给定一个图，每次都选择一个无入度（没有入边）的节点加入序列中，并删除该节点的出边

最终得到的序列就是一个拓扑排序之后的序列

  • 每次删除出边后，都可能形成新的无入度的节点

因此，针对同一棵树的拓扑排序序列，可能有多种不同的情况

5.最小生成树算法

生成树的概念参考 1.8 生成树，最小生成树即让生成树中所有边的权值加起来最小

5.1 普里姆Prim

image-20221206164945471

如图中所示，我们先根据这个树的结构构造三个数组

  • nearest代表和这个节点最近的节点（默认为-1）
  • lowcost代表和这个节点最近节点的权值（默认为无穷大）
  • mark是一个bool数组，标识该节点是否已经加入到最小生成树

当我们每从图中取出一个节点的时候，就需要更新这三个表

如图，当我们取走0之后，就需要更新和0连通的三个节点，其中nearest代表刚刚删除掉的节点0，lowcost代表它们和0相连边的权值；同时要把mark中0改为true，表明0已经加入生成树了

image-20221206165820864

第二次选取的时候，遍历lowcost表，找到权值最小的边为(0,2)权值为1。此时就把2加入进去，并更新与2相连的节点3（注，必须要权值更小才需要更新）

image-20221206170707450

依次遍历，直到所有节点都加入了最小生成树（左下角的图）

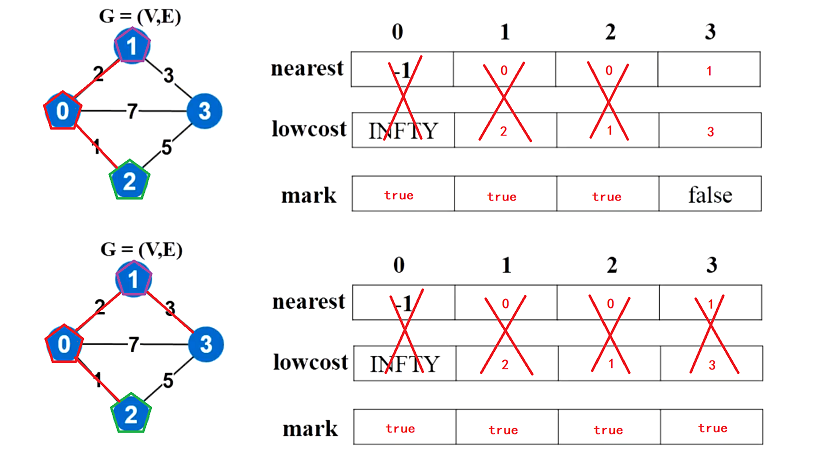
image-20221206171723913

该算法的时间复杂度为O(N^2)，只与节点的数量N有关

5.2 克鲁斯卡尔Kruskal

image-20221206172343754

构建一个和原图一样的节点图（无边）在原图中查找权值最小的边，判断其节点是否已经相同，如果没有形成环，则加入到最小生成树的图中

判断是否成环可以通过并查集解决

如下图，先遍历所有边，发现(0,2)的权值最小，判断该边加入后并不会使生成树形成环，则加入该边

  • 下图中(0,2)之间的边1已经移动到了T图上
  • 同时将0和2加入到同一个并查集的合集内

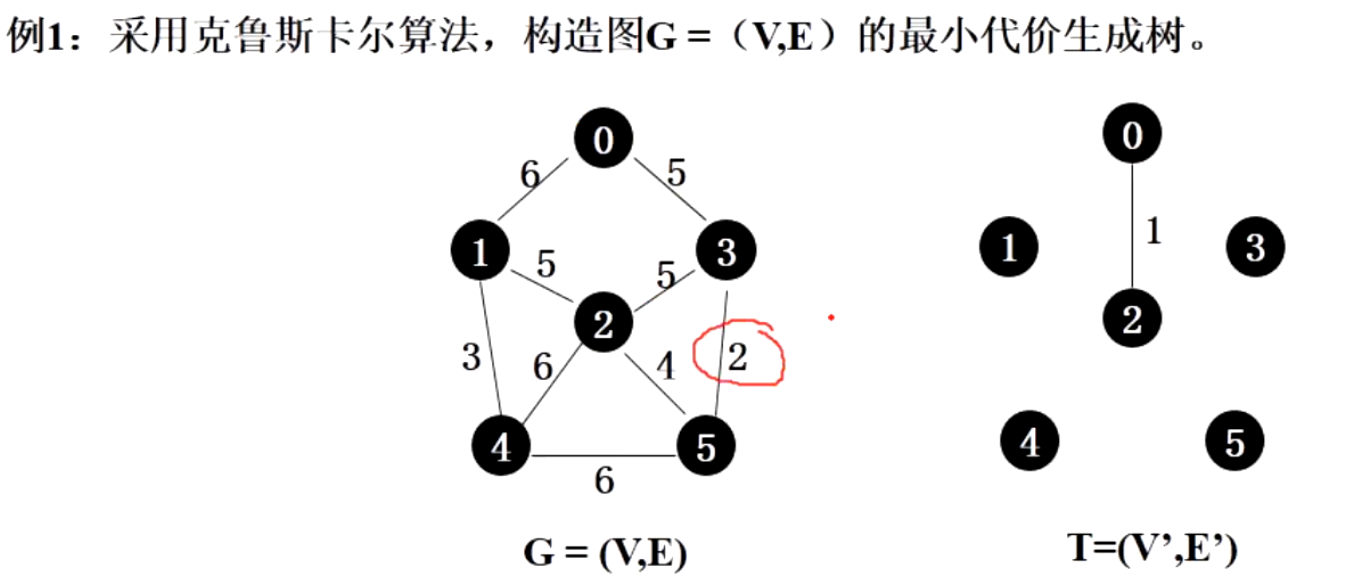
image-20221206172624950

同理继续找权值最小的边，加入到生成树中。如下，将3边移动到右图。

image-20221206172822375

此时我们遇到了3条权值最小的边，权值都为5。此时可以随便加入一条边即可（不能使生成树成环）

如下图中(0,3)和(2,3)的边加入后会使图成环，不能选择该边

  • 并查集中0、2、3、5已经在一个集合中，此时判断(0,3)在一个集合，该边不能加入；(2,3)在一个集合中，该边不能加入

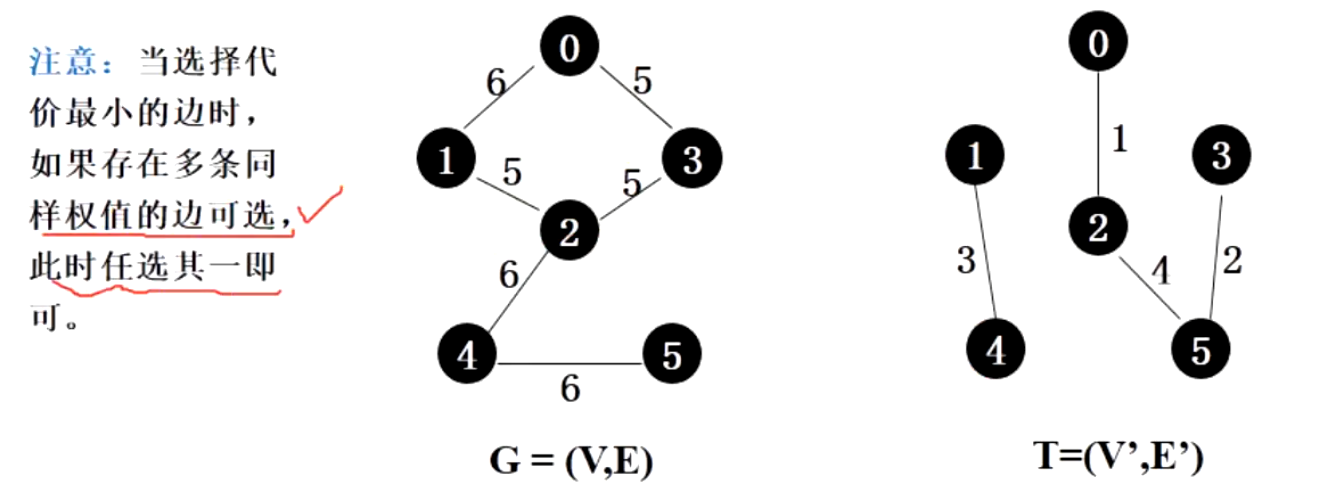
image-20221206172909839

应该选择(1,2)这条边，其不会让树成环

image-20221206173200557

此时所有边都已经连起来了，最小生成树生成成功

算法分析

image-20221206173648882

image-20221206173706988

该算法的时间复杂度为O(E*logE)，其中E为边的数目

6.最短路径

带权有向图中，把一条路径（仅考虑简单路径）上所经边的权值之和定义为该路径的路径长度

从源点到终点可能不止一条路径，把路径长度最短的那条路径称为最短路径

6.1 单源最短路径

思路有些类似并查集，path数组中存放的是每一个节点的上一条路径，若下标1处存放0，则代表是从0走到1。同时d数组中标识从0走到下标1的长度。

image-20221206184617517

把1加到s序列之后，发现0到节点2的路径长度缩短了，从原本的(0,2)的6变成了现在(0,1)+(1,2)的4+1=5，长度缩短，对应d数组中下标2处也需要更新

继续下去，直到U数组中没有节点，S数组中节点满，即可获得一个从0出发到任何节点的单源最短路径

6.1.1 狄克斯特拉算法Dijkstra

求解单源最短路径问题的算法

前提：给定一个带权有向图G和源点v，限定各边上的权值大于等于0

基于定理：最短路径上的顶点的最短路径就是该路径

理解：现有一条v到u的最短路径v->……->a->u，那么v到a的最短路径即为v->……->a

算法思路

把图G中的顶点集合V分成两部分：

第一部分，为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径v，……，u，就将u加入到集合S中，直到全部顶点都加入到S中，算法结束）

第二部分，为其余未求出最短路径的顶点集合（用U表示）

过程：

  1. 初始化：S只包含源点即S={v}，v的最短路径为0。U包含除v以外的其他顶点，U中顶点i距离为边上的权值（若v与i直接相连）或∞（v与i不是直接相连）

image-20221215202813428

  1. 从U中选取一个距离v最小的顶点u，把u加入S中（该选定的距离就是v到u的最短路径长度）

image-20221215203045922

image-20221215203110663

  1. 以u为新考虑的中间点，修改U中各顶点i的最短路径长度

若从源点v到顶点 i的最短路径长度（经过顶点u）比原来最短路径长度（不经过顶点u）短，则修改顶点 i的最短路径长度

image-20221215203341139

  1. 重复2、3步，直至所有顶点都包含在S中

代码设计

着重解决两个问题：

  1. 如何存放最短路径长度？

用一维数组d[i]存储。源点v默认，d[i]表示源点到顶点i的最短路径长度

如d[2]=12表示源点到顶点2的最短路径长度为12

  1. 如何存放最短路径？

用一维数组path[]存储。path数组中所存储的数组代表当前顶点在最短路径中的前驱顶点

如path[3]=1，表示在最短路径中，顶点3的前驱顶点是顶点1

算法演示

image-20221215204311623

这是初始化状态

发现数组d中顶点1距离源点距离最近，那么就将顶点1加入到S中

image-20221215204643536

这时，我们需要更新剩余点的最短路径长度和最短路径

显然，顶点2，3，4，5，6并不会都做更新。只有与顶点1直接相连的顶点才有可能会受影响。在上图中会受影响的为顶点2和顶点4

image-20221215204857064

原本顶点2的最短路径长度是6，最短路径是<0,2>。现在由于顶点1的引入，最短路径长度变为5，最短路径变为<0,1>,<1,2>

顶点4同理！

至此，就完成了一次顶点的引入。下面重复上述操作至所有顶点都在S中即可

下面是全过程：

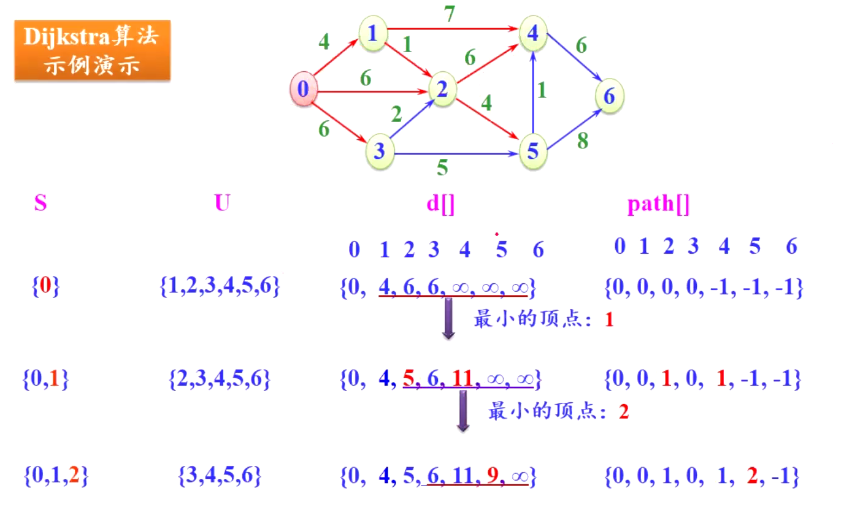
image-20221215210605089

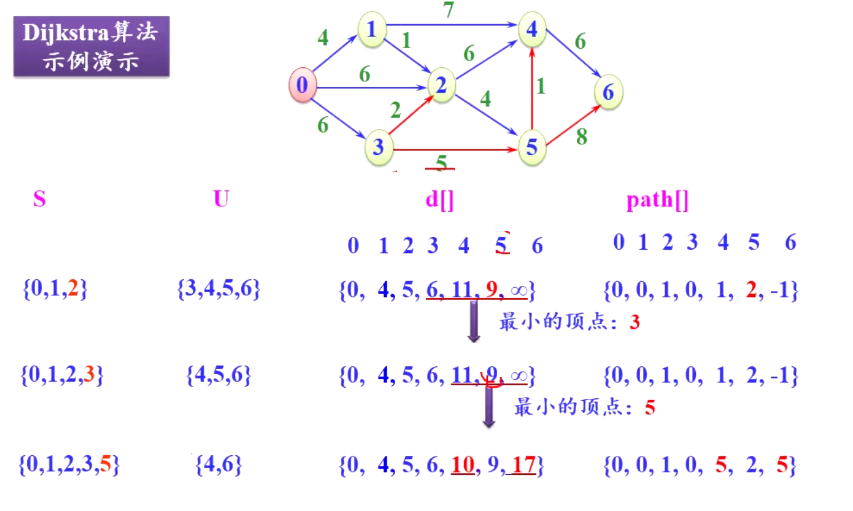
image-20221215210729969

image-20221215210949302

总结一下：在更新d和path数组时，只有与本次引入S中的顶点i直接相连的后驱顶点才有可能发生改变，其余顶点是不可能变的

现在我们利用d和path数组来求解最短路径长度和最短路径：

  • 求源点0到终点6的最短路径长度

即为d[6]的值，为16

  • 求0到6的最短路径

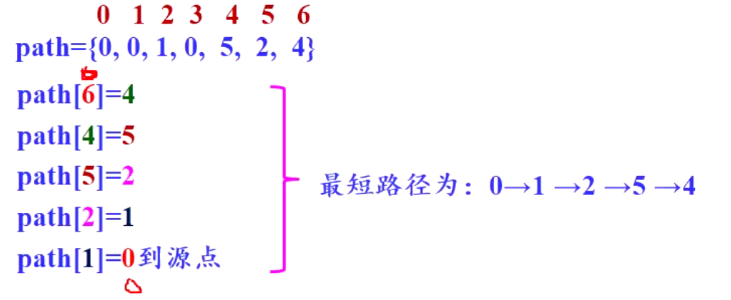
image-20221216102425727

从终点往源点找

时间复杂度

时间复杂度为 O(n2)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/403470.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JDBC的API详解

JDBC的API详解

&#x1f34e;道阻且长&#xff0c;行则将至。&#x1f353; 目录 一、DriverManager 驱动管理类 1.注册驱动 2.获取数据库连接 二、Connection 数据库连接对象 1.获取执行对象 2.事务管理 三、Statement 1.执行DDL、DML语句 2.执行DQL语句 四、ResultSet 以JDBC快速…
阅读更多...
【漏洞复现】Grafana任意文件读取（CVE-2021-43798）

【漏洞复现】Grafana任意文件读取（CVE-2021-43798）

docker环境搭建 #进入环境 cd vulhub/grafana/CVE-2021-43798#启动环境&#xff0c;这个过程可能会有点慢&#xff0c;保持网络通畅 docker-compose up -d#查看环境 docker-compose ps直接访问虚拟机 IP地址:3000 目录遍历原理 目录遍历原理&#xff1a;攻击者可以通过将包含…
阅读更多...
CNCF x Alibaba云原生技术公开课 第七章 应用编排与管理：Job和DaemonSet

CNCF x Alibaba云原生技术公开课 第七章 应用编排与管理：Job和DaemonSet

1、Job&#xff1a;管理任务的控制器 概念 首先 kubernetes 的 Job 是一个管理任务的控制器&#xff0c;它可以创建一个或多个 Pod 来指定 Pod 的数量&#xff0c;并可以监控它是否成功地运行或终止&#xff1b;可以根据 Pod 的状态来给 Job 设置重置的方式及重试的次数&…
阅读更多...
【Qt网络编程】实现TCP协议通信

【Qt网络编程】实现TCP协议通信

文章目录概要&#xff1a;本期主要讲解QT中对于TCP协议通信的实现。一、TCP协议二、Qt中TCP协议处理1.QTcpSocket2.QTcpServer三、Qt实现TCP通信1.客户端2.服务器端结尾概要&#xff1a;本期主要讲解QT中对于TCP协议通信的实现。 一、TCP协议 传输控制协议&#xff08;TCP&am…
阅读更多...
有哪些值得推荐的办公软件下载网站

有哪些值得推荐的办公软件下载网站

新买了电脑之后&#xff0c;我们需要安装一些常用的办公软件才能方便我们的办公使用。很多小白不知道在哪里下载办公软件比较好&#xff0c;下面小编就来为大家分享几个值得推荐的办公软件下载网站。 1.常用软件下载 对于常用软件如果我们通过百度搜索&#xff0c;能够辨别官方…
阅读更多...
【2】Dijkstra与SPFA等常见最短路算法的分析与比较——Bellman-Ford与SPFA

【2】Dijkstra与SPFA等常见最短路算法的分析与比较——Bellman-Ford与SPFA

合集目录&#xff1a; 前言 一、Dijkstra 二、Bellman-Ford与SPFA&#xff08;本文&#xff09; 三、Dijkstra与SPFA的比较 四、Floyd 五、启发式搜索 Bellman-Ford 1. 算法介绍 The algorithm was first proposed by Alfonso Shimbel (1955), but is instead named af…
阅读更多...
哪个牌子的洗地机耐用？耐用的洗地机推荐

哪个牌子的洗地机耐用？耐用的洗地机推荐

作为当下非常热销的洗地机&#xff0c;它不仅解放了双手&#xff0c;使用也非常的便捷。是生活品质提高的最好代表&#xff0c;但是面对市面上让人眼花缭乱的洗地机&#xff0c;挑选几个来回都决定不了到底入手哪个好&#xff01;为了能帮助大家选购到合适的洗地机&#xff0c;…
阅读更多...
gcc 编译的过程

gcc 编译的过程

#include <stdio.h> #define PI 3.14 int main(int argc, char const *argv[]) { //打印IP的值printf("PI %lf\n", PI);return 0; }编译的过程&#xff1a;预处理、编译、汇编、链接1.预处理&#xff1a;宏替换、删除注释、头文件包含、条件编译 -E &#xf…
阅读更多...
问心 | 再看token、session和cookie

问心 | 再看token、session和cookie

什么是cookie HTTP Cookie&#xff08;也叫 Web Cookie或浏览器 Cookie&#xff09;是服务器发送到用户浏览器并保存在本地的一小块数据&#xff0c;它会在浏览器下次向同一服务器再发起请求时被携带并发送到服务器上。 什么是session Session 代表着服务器和客户端一次会话…
阅读更多...
Paddle项目调试记录

Paddle项目调试记录

PaddlePaddle是百度公司提出的深度学习框架。近年来深度学习在很多机器学习领域都有着非常出色的表现&#xff0c;在图像识别、语音识别、自然语言处理、机器人、网络广告投放、医学自动诊断和金融等领域有着广泛应用。面对繁多的应用场景&#xff0c;深度学习框架有助于建模者…
阅读更多...
MyBatis-Plus(狂神)

MyBatis-Plus(狂神)

一.特点 无侵入&#xff1a;只做增强不做改变&#xff0c;引入它不会对现有工程产生影响&#xff0c;如丝般顺滑损耗小&#xff1a;启动即会自动注入基本 CURD&#xff0c;性能基本无损耗&#xff0c;直接面向对象操作强大的 CRUD 操作&#xff1a;内置通用 Mapper、通用 Serv…
阅读更多...
GDB调试快速入门

GDB调试快速入门

什么是GDB&#xff1a; GDB - - - (GNU symbolic debugger)是Linux平台下最常用的一款程序调试器。 自己的Linux是否安装GDB? 一般来说&#xff0c;使用Ubuntu的话&#xff0c;系统就会自带的有GDB调试器的 命令窗口输入如下命令可以查看是否安装了gdb&#xff1a; gdb -v …
阅读更多...
制作一个简单的信用卡验证表

制作一个简单的信用卡验证表

下载：https://download.csdn.net/download/mo3408/87559584 效果图： 您可以从文章顶部附近的下载按钮获取该项目的完整代码。这些文件的概述如下所示： 我们需要将两个 .css 文件和两个 .js 文件包含在我们的 HTML 中。所有其他资源，例如 Bootstrap 框架、jQuery 和 Web 字…
阅读更多...
SecureCRT 安装并绑定ENSP设备终端

SecureCRT 安装并绑定ENSP设备终端

软件下载链接链接&#xff1a;https://pan.baidu.com/s/1WFxmQgaO9bIiUTwBLSR4OA?pwd2023 提取码&#xff1a;2023 CRT安装&#xff1a;软件可以从上面链接进行下载&#xff0c;下载完成后解压如下&#xff1a;首先双击运行scrt-x64.8.5.4 软件&#xff0c;进行安装点击NEXT选…
阅读更多...
PMP项目管理项目资源管理

PMP项目管理项目资源管理

目录1 项目资源管理概述2 规划资源管理3 估算活动资源4 获取资源5 建设团队6 管理团队7 控制资源1 项目资源管理概述 项目资源管理包括识别、获取和管理所需资源以成功完成项目的各个过程&#xff0c;这些过程有助于确保项目经理和项目团队在正确的时间和地点使用正确的资源。…
阅读更多...
Nacos未授权访问漏洞（CVE-2021-29441）

Nacos未授权访问漏洞（CVE-2021-29441）

目录漏洞描述影响范围环境搭建漏洞复现声明&#xff1a;本文仅供学习参考&#xff0c;其中涉及的一切资源均来源于网络&#xff0c;请勿用于任何非法行为&#xff0c;否则您将自行承担相应后果&#xff0c;本人不承担任何法律及连带责任。加粗样式 漏洞描述 Nacos 是阿里巴巴…
阅读更多...
Redis缓存双写一致性

Redis缓存双写一致性

目录双写一致性Redis与Mysql双写一致性canal配置流程代码案例双写一致性理解缓存操作细分缓存一致性多种更新策略挂牌报错,凌晨升级先更新数据库,在更新缓存先删除缓存,在更新数据库先更新数据库,在删除缓存延迟双删策略总结双写一致性 Redis与Mysql双写一致性 canal 主要是…
阅读更多...
vuex3的介绍与state、actions和mutations的使用

vuex3的介绍与state、actions和mutations的使用

一、定义官网&#xff1a;Vuex 是什么&#xff1f; | Vuex (vuejs.org)Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态&#xff0c;并以相应的规则保证状态以一种可预测的方式发生变化。二、安装cdn<script src"/path/…
阅读更多...
[手撕数据结构]栈的深入学习-java实现

[手撕数据结构]栈的深入学习-java实现

CSDN的各位uu们你们好,今天千泽带来了栈的深入学习,我们会简单的用代码实现一下栈, 接下来让我们一起进入栈的神奇小世界吧!0.速览文章一、栈的定义1. 栈的概念2. 栈的图解二、栈的模拟实现三.栈的经典使用场景-逆波兰表达式总结一、栈的定义 1. 栈的概念 栈&#xff1a;一种…
阅读更多...
Optimizers for Deep Learning

Optimizers for Deep Learning

文章目录一、Some NotationsWhat is Optimization about?二、SGDSGD with Momentum(SGDM)Why momentum?三、AdagradRMSProp四、AdamSWATS [Keskar, et al., arXiv’17]Towards Improving AdamTowards Improving SGDMRAdam vs SWATSLookahead [Zhang, et al., arXiv’19]Momen…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023