-
我们先介绍 Float32、Float16、BFloat16 的 浮点数表示方法
-
然后根据浮点数表示,来分析总结他们是怎么控制 精度和 数值范围 的
-
最后再来对比的说明 Float32、Float16、BFloat16 的 应用场景 和 硬件支持
1、浮点数的表示方法
-
Float32 : 单精度浮点数格式
-
使用 32位(4字节)来表示一个浮点数
-
遵循 IEEE 754标准,32位 包括 1 位符号位、8 位指数部分和 23 位尾数部分
-
-
Float16:半精度浮点数格式,
-
使用 16位(2字节)来表示一个浮点数
-
遵循 IEEE 754标准,16位 包括 1 位符号位、5 位指数部分和 10 位尾数部分
-
-
BFloat16: Brain Floating Point 16-bit
-
使用 16位(2字节)来表示一个浮点数
-
不遵循 IEEE 754标准,16位 包括 1 位符号位、8 位指数部分 和 7 位尾数部分
-
| 数据类型 | 一共位数 | 符号位数(Sign) | 指数位数(Exponent) | 尾数位数(Mantissa) |
| Float32 | 32 | 1 | 8 | 23 |
| Float16 | 16 | 1 | 5 | 10 |
| BFloat16 | 16 | 1 | 8 | 7 |
float32 结构为 :
S | EEEEEEEE | MMMMMMMMMMMMMMMMMMMMMMM
float16 结构为 :
S | EEEEE | MMMMMMMMMM
bfloat16 结构为 :
S | EEEEEEEE | MMMMMMMMMMMM
浮点数的值 通过以下公式计算:
其中 :
-
S:符号位,表示数字的正负:0 为正,1 为负
-
Mantissa:尾数部分
-
Exponent:指数部分,表示 2 的幂次
-
Bias:指数的偏置
-
float32的 Bias 为 127 -
float16的 Bias 为 15 -
bfloat16的 Bias 为 127
-
下面我们具体来举例说明 浮点数的表示
1)float32
float32 :32位浮点数,通常称为 单精度浮点数
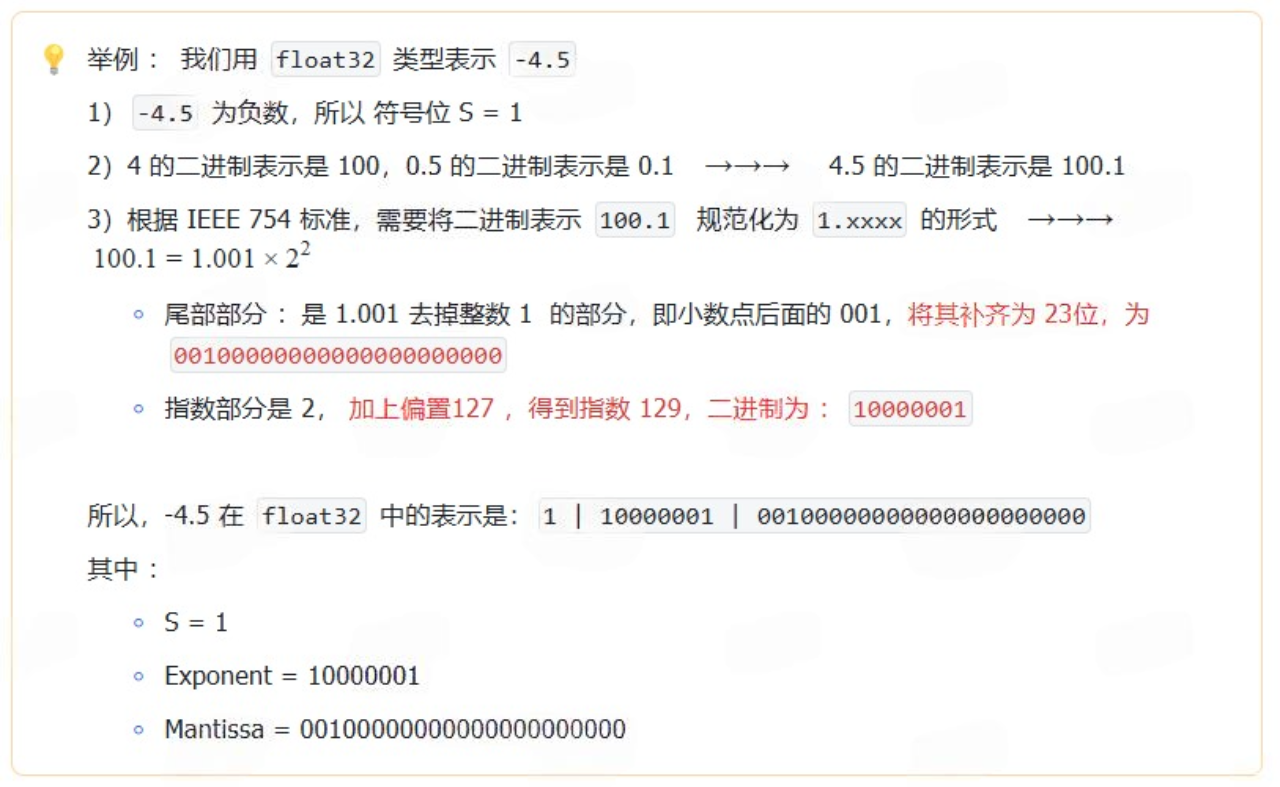
2)float16
float16 是 16 位浮点数,通常称为 半精度浮点数
float16的浮点数表示方法 与 float32 的表示方法类似,只不过在表示上有较小的精度和范围。

3)bfloat16
BFloat16 主要用于 深度学习训练阶段,特别是在需要保持与 Float32 类似的 数值范围 的同时,减少内存占用(精度比较低)

2、指数偏置 Bias
指数的偏置(Bias) 主要是用来 控制指数部分的正负。

由上面例子可知 :
-
实际指数 是 -1,它表示的是浮点数的真实指数。
-
实际指数 -1 加上 指数偏置 127 后,得到存储的指数 126,它的二进制形式 01111110 是存储在浮点数表示中的值。
所以,指数偏置的作用:是将原本可能为负的指数值 (-1),转换为 无符号整数(126),以便于计算机在表示时能够方便地使用无符号整数表示 指数部分。
3、精度 与 数值范围
1)指数部分 (Exponent) 控制数据范围

结论 :指数部分位数越多,可以表示的 数据范围越大
2)尾数部分 (Mantissa) 控制精度

结论 :尾数部分位数越多,可以表示的 精度越高

有效数字:指的是在浮点数表示中,能够精确表达的数字。即,从最左边非零数字到最后一位数字的所有数字
-
123.45 有 5 个有效数字:1, 2, 3, 4, 5
-
0.00456 有 3 个有效数字:4, 5, 6
-
400 有 3 个有效数字:4, 0, 0
4、应用场景 与 硬件支持
应用场景:
-
Float32:最常见的浮点数类型,适用于大多数机器学习的训练阶段和推理阶段,适合精度要求高的任务 -
Float16: 主要用于推理阶段, 数值精度较低,可通过硬件加速提高计算效率 -
BFloat16:主要用于深度学习训练阶段,尤其是在需要保持数值范围的同时(BFloat16保留了和float32类似的数值范围),又想要降低内存需求的任务,旨在减少内存占用和加速计算
硬件支持 :
-
Float32:大多数现代硬件(如 CPU 和 GPU)都对float32提供良好的支持 -
Float16:一些 GPU(尤其是 NVIDIA 的 Volta 及之后的架构,如 V100、A100、T4)对float16有硬件支持,可以显著加速训练和推理 -
BFloat16:bfloat16在某些硬件(特别是 Google 的 TPU 以及 Intel 的处理器)上得到硬件支持,用于加速深度学习的训练和推理