文章目录
- 一、Some Notations
- What is Optimization about?
- 二、SGD
- SGD with Momentum(SGDM)
- Why momentum?
- 三、Adagrad
- RMSProp
- 四、Adam
- SWATS [Keskar, et al., arXiv’17]
- Towards Improving Adam
- Towards Improving SGDM
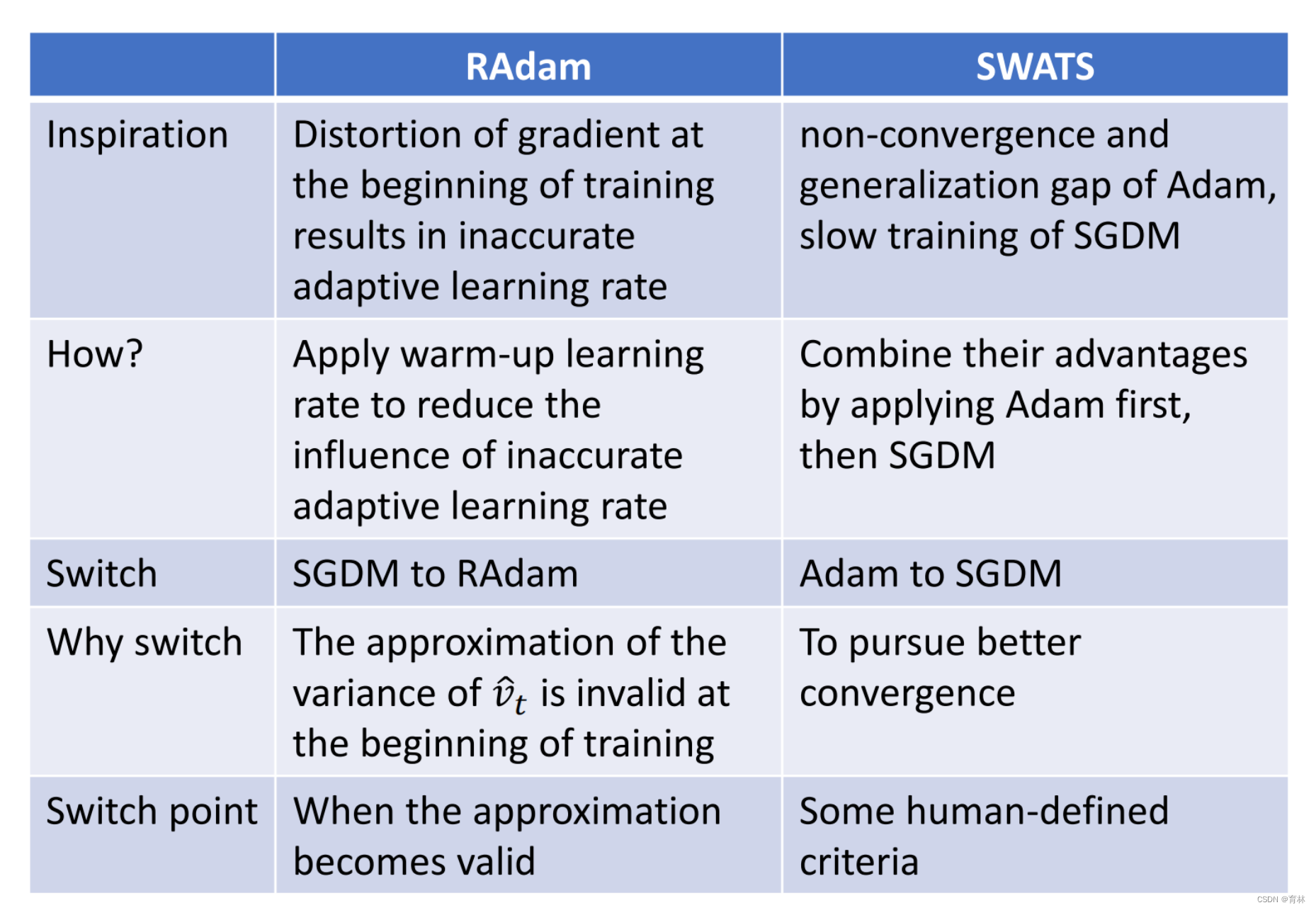
- RAdam vs SWATS
- Lookahead [Zhang, et al., arXiv’19]
- Momentum recap
- Can we look into the future
- 五、optimizer
- L2
- AdamW & SGDW with momentum
- Something helps optimization
- 总结
- Advices:
一、Some Notations
𝜃𝑡: model parameters at time step 𝑡
• ∇𝐿(𝜃𝑡) or 𝑔𝑡 : gradient at 𝜃𝑡 , used to compute 𝜃𝑡+1
𝑚𝑡+1: momentum accumulated from time step 0 to
time step 𝑡, which is used to compute 𝜃𝑡+1
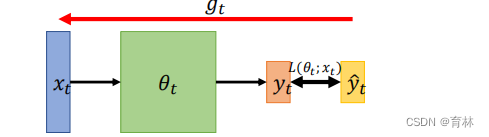
What is Optimization about?
Find a 𝜃 to get the lowest σ𝑥 𝐿(𝜃; 𝑥)
Or, Find a 𝜃 to get the lowest 𝐿(𝜃)

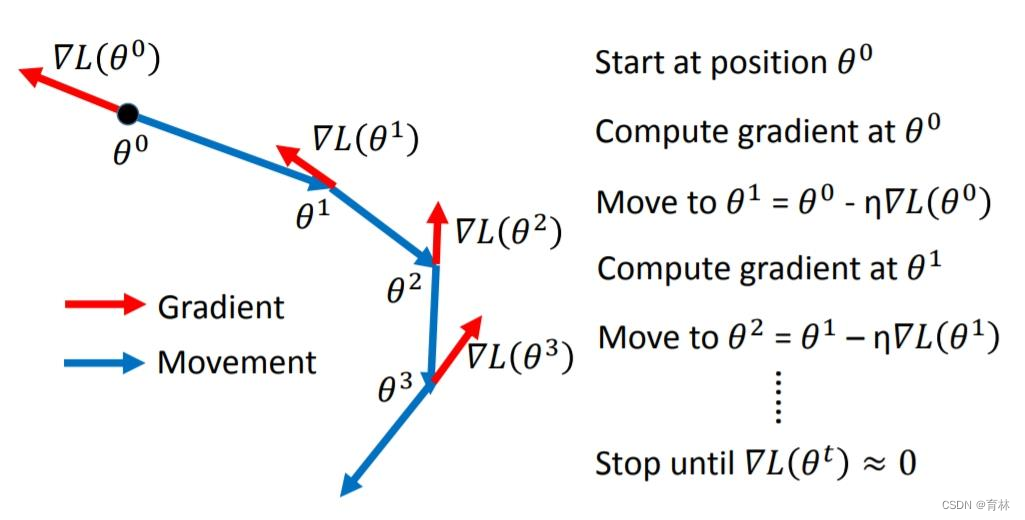
二、SGD
SGD with Momentum(SGDM)
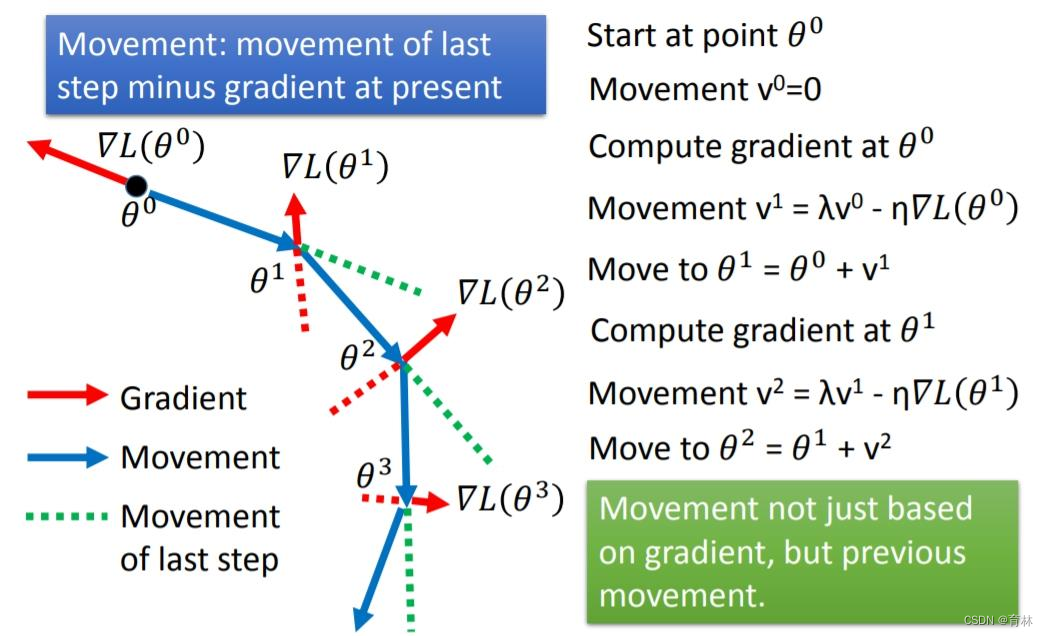


Why momentum?
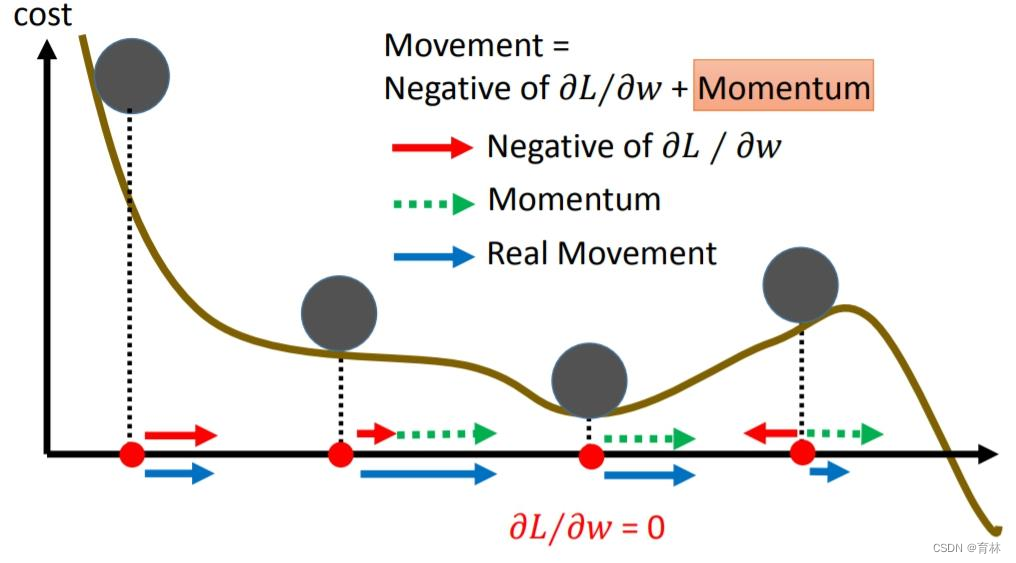
三、Adagrad
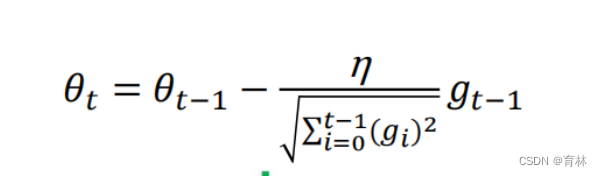
What if the gradients at the first few time steps are extremely large…
RMSProp
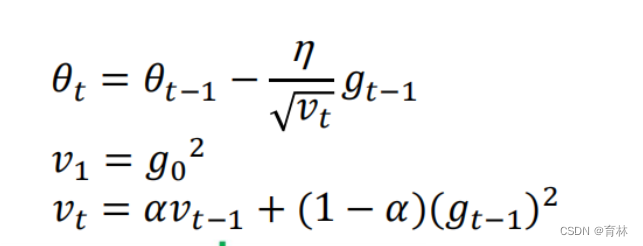
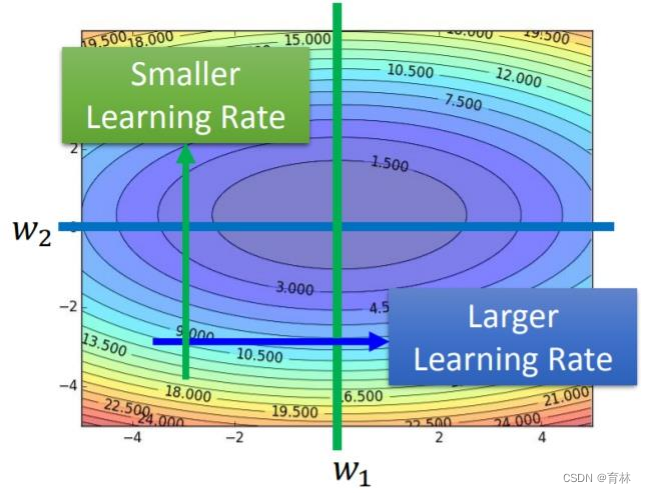
Exponential moving average (EMA) of squared gradients is not monotonically increasing
四、Adam

Adam vs SGDM
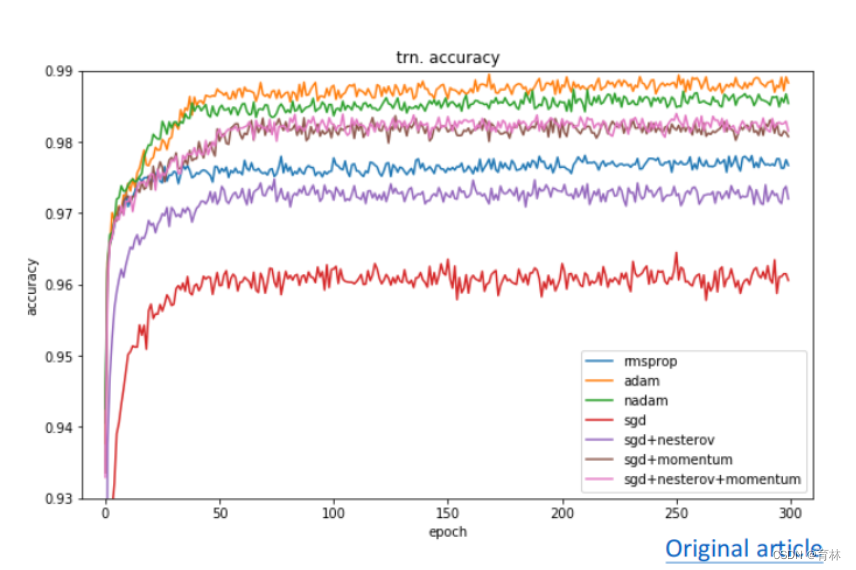
Adam vs SGDM
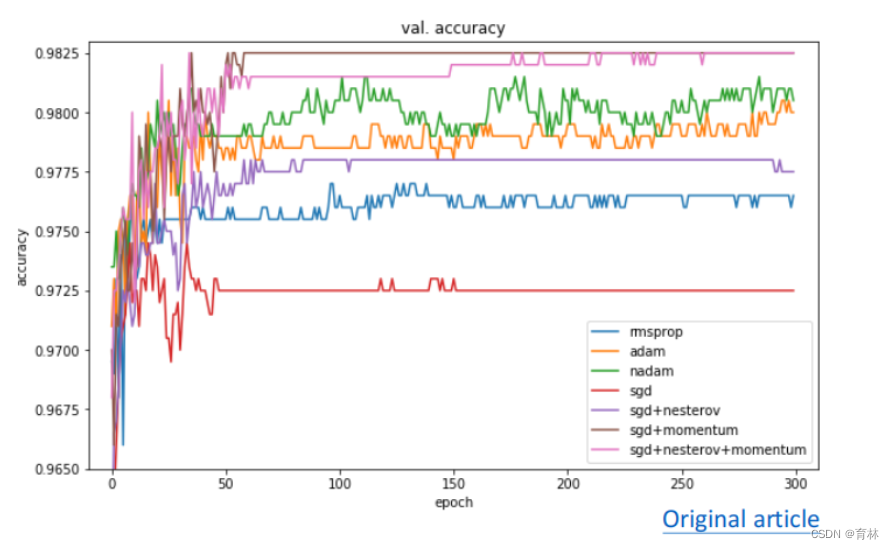
Adam vs SGDM
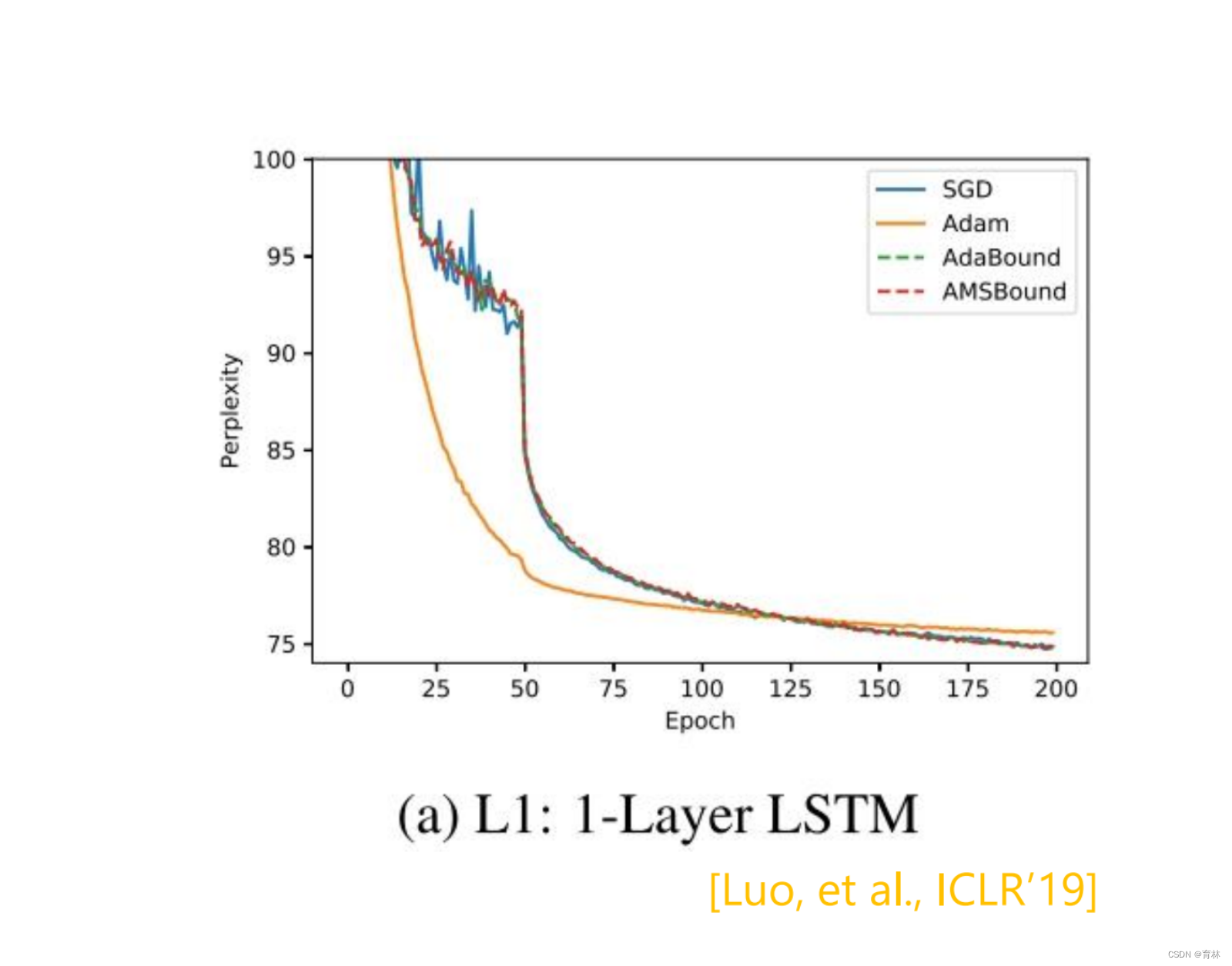
Adam:fast training, large generalization gap, unstable
• SGDM:stable, little generalization gap, better convergence(?)
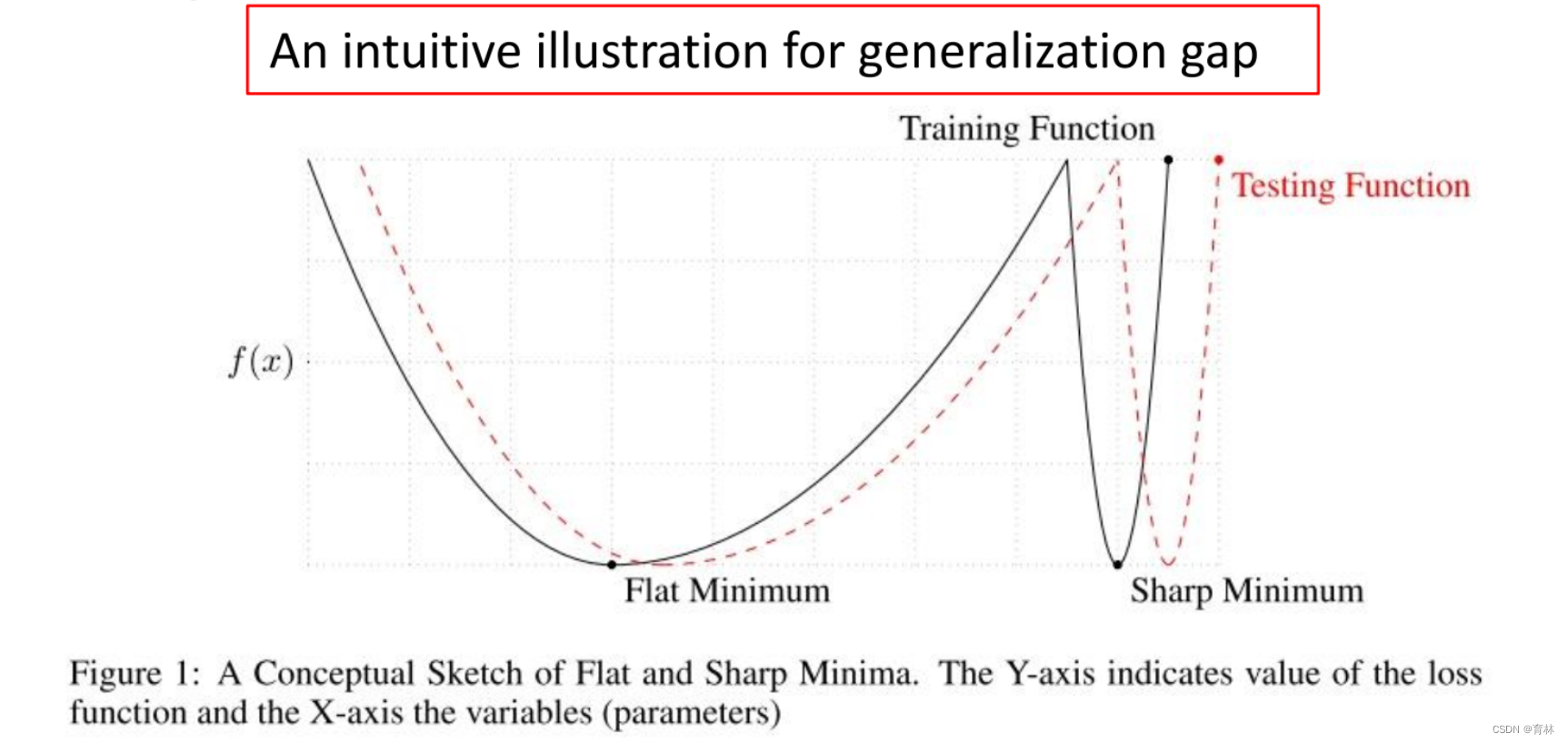
SWATS [Keskar, et al., arXiv’17]
Begin with Adam(fast), end with SGDM
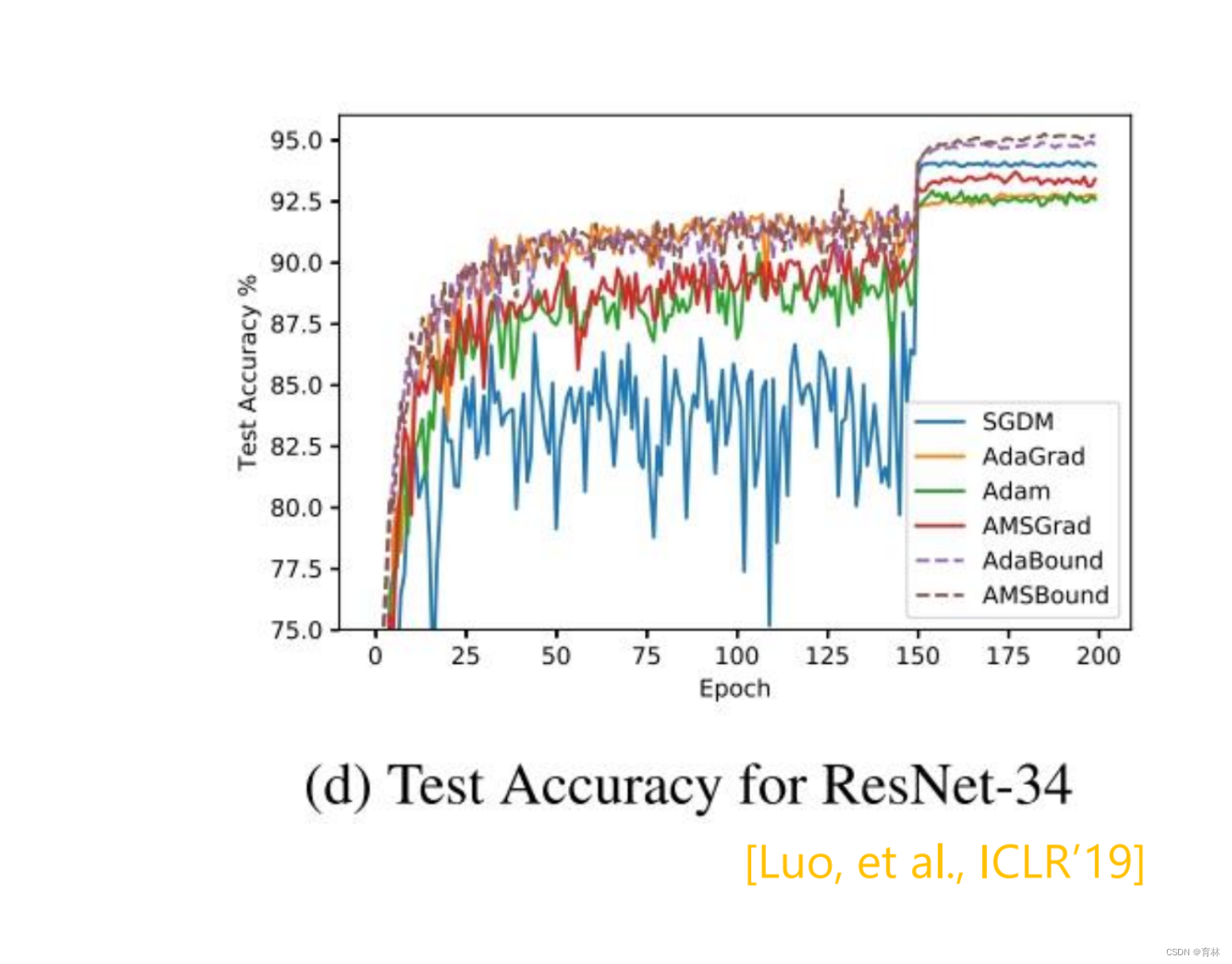
Towards Improving Adam
Trouble shooting:
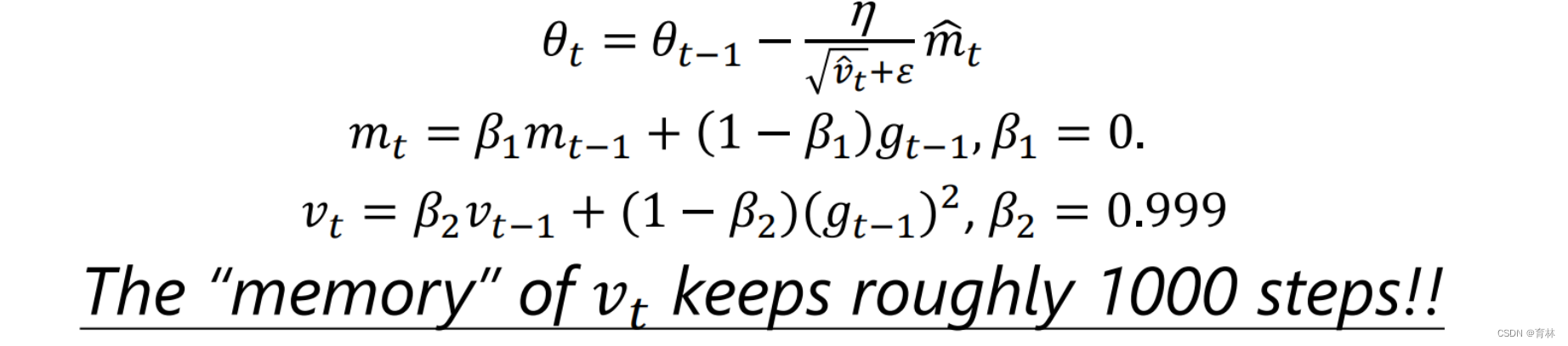
The “memory” of 𝑣𝑡 keeps roughly 1000 steps!!
In the final stage of training, most gradients are small and non-informative, while some mini-batches provide large informative gradient rarely

Towards Improving SGDM
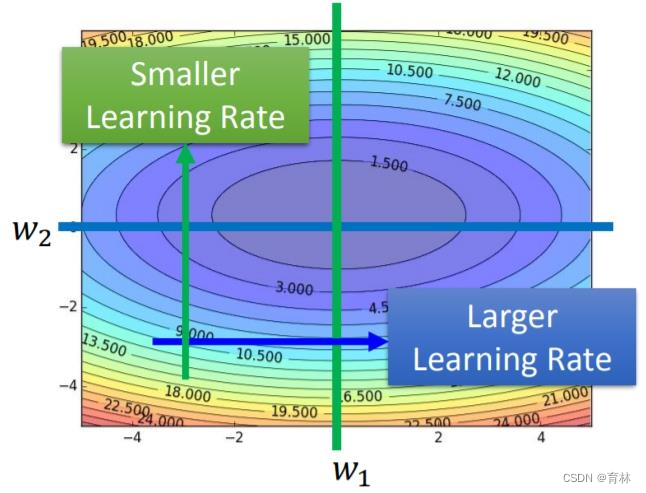
Adaptive learning rate algorithms:dynamically adjust learning rate over time
SGD-type algorithms:fix learning rate for all updates… too slow for small learning rates and bad result for large learning rates
Cyclical LR [Smith, WACV’17]
• learning rate:decide by LR range test
• stepsize:several epochs
• avoid local minimum by varying learning rate

• SGDR [Loshchilov, et al., ICLR’17]
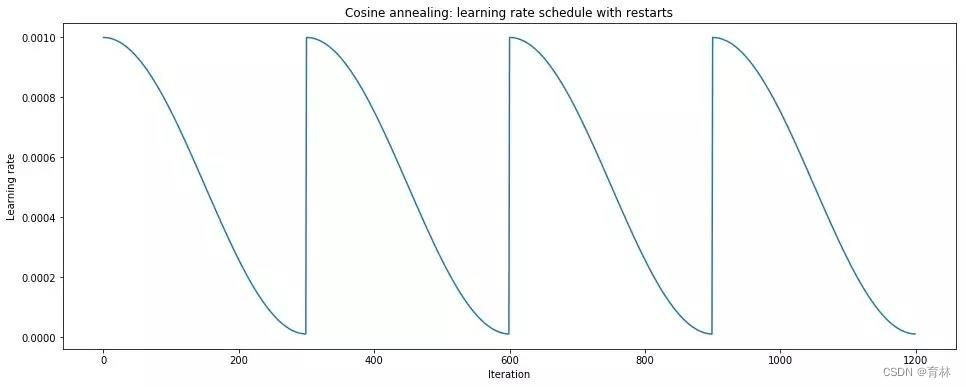
Adam need warm-up

Experiments show that the gradient distribution distorted in the first 10 steps
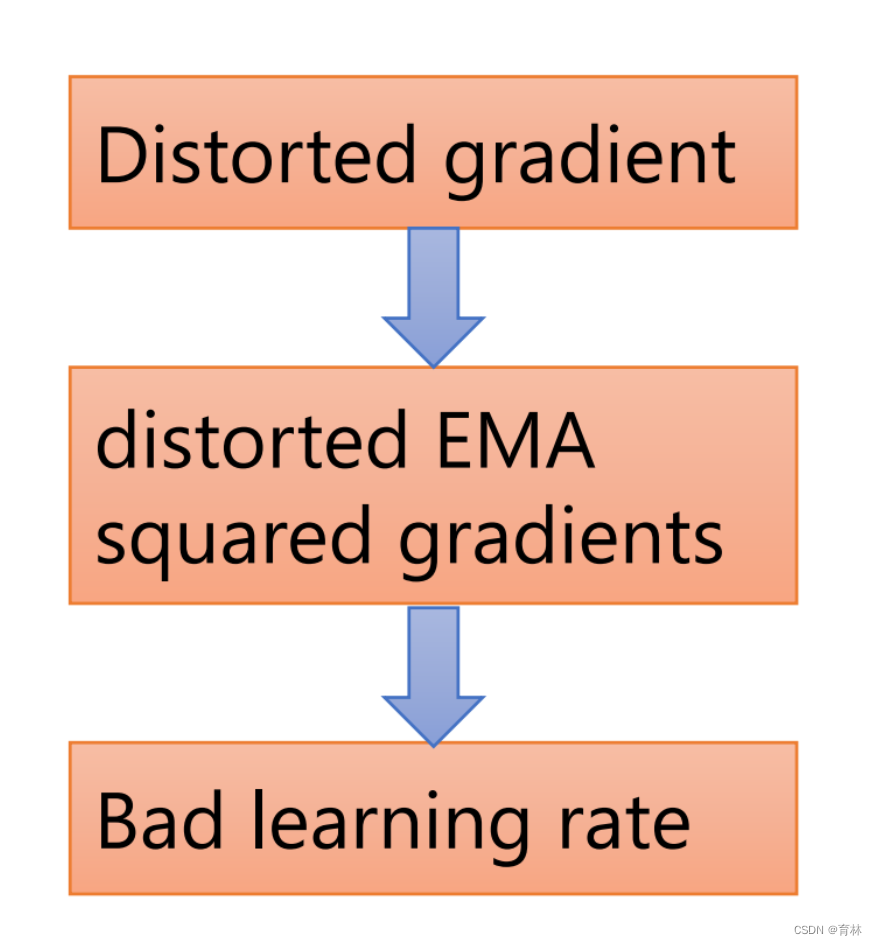

Keep your step size small at the beginning of training helps to reduce the variance of the gradients
RAdam [Liu, et al., ICLR’20]

1 、effective memory size of EMA
2、max memory size (t → ∞)
3、**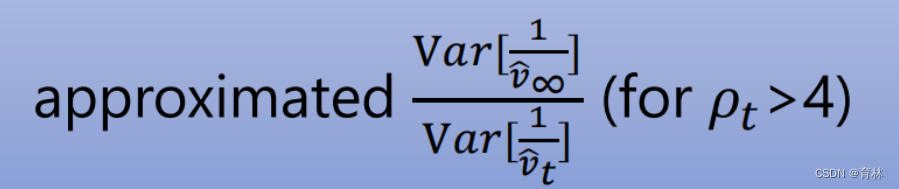
**
RAdam vs SWATS
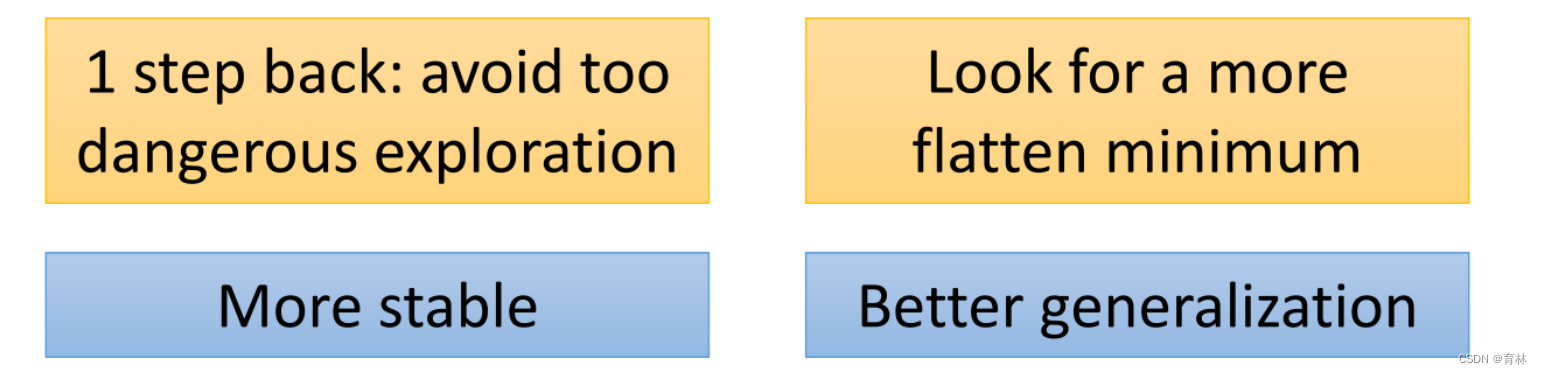
Lookahead [Zhang, et al., arXiv’19]

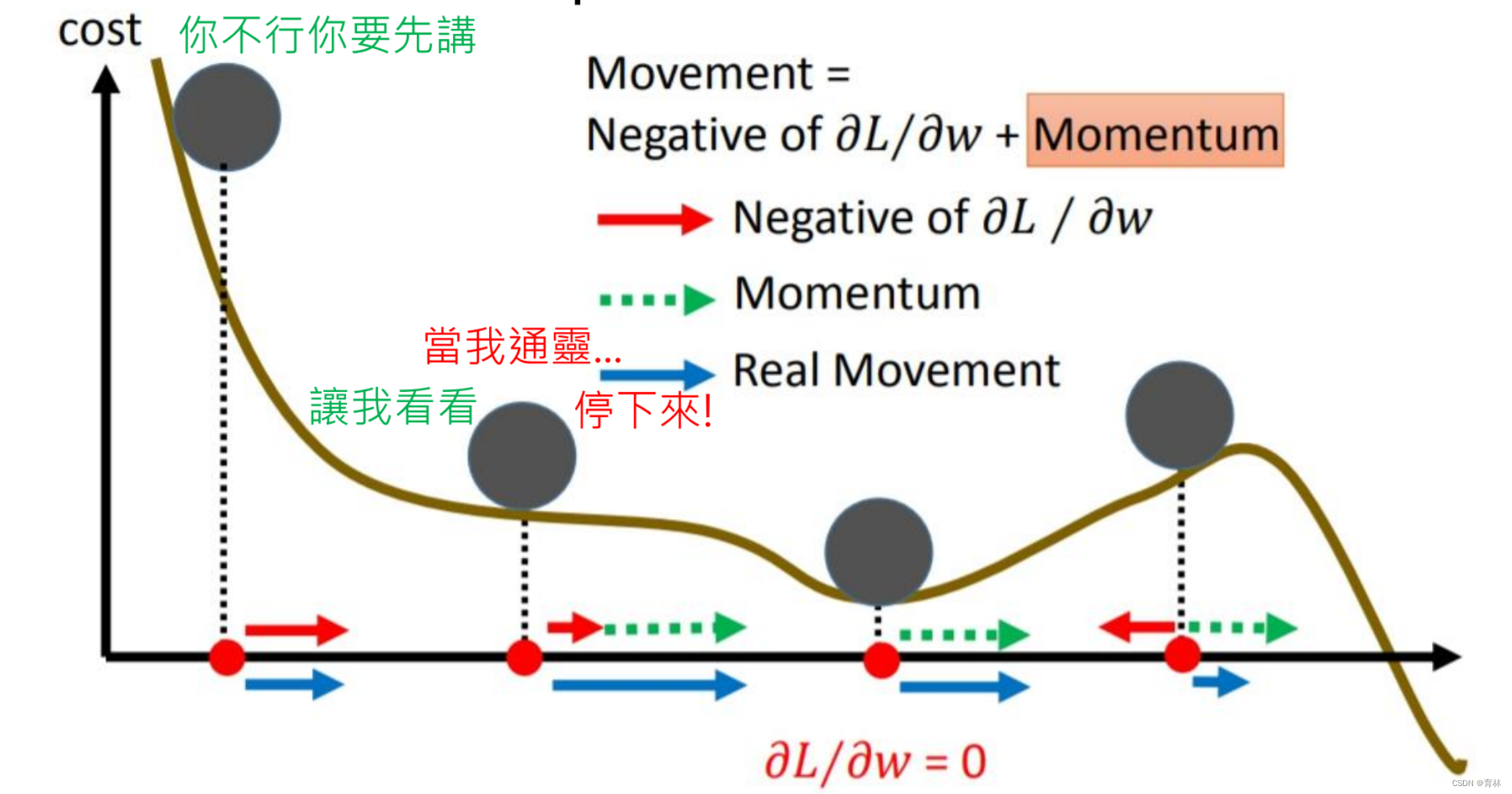
Momentum recap
Can we look into the future
Nesterov accelerated gradient (NAG) [Nesterov, jour Dokl. Akad. Nauk SSSR’83]
SGDM:
𝜃𝑡 = 𝜃𝑡−1 − 𝑚𝑡
𝑚𝑡 = 𝜆𝑚𝑡−1 + 𝜂∇𝐿(𝜃𝑡−1)
Look into the future:
𝜃𝑡 = 𝜃𝑡−1 − 𝑚𝑡
𝑚𝑡 = 𝜆𝑚𝑡−1 + 𝜂∇𝐿(𝜃𝑡−1 − 𝜆𝑚𝑡−1)
Nesterov accelerated gradient (NAG):
𝜃𝑡 = 𝜃𝑡−1 − 𝑚𝑡
𝑚𝑡 = 𝜆𝑚𝑡−1 + 𝜂∇𝐿(𝜃𝑡−1 − 𝜆𝑚𝑡−1)
𝐿𝑒𝑡 𝜃𝑡′ = 𝜃𝑡 − 𝜆𝑚𝑡
= 𝜃𝑡−1 − 𝑚𝑡 − 𝜆𝑚𝑡
= 𝜃𝑡−1 − 𝜆𝑚𝑡 − 𝜆𝑚𝑡−1 − 𝜂∇𝐿(𝜃𝑡−1 − 𝜆𝑚𝑡−1)
= 𝜃𝑡−1’ − 𝜆𝑚𝑡 − 𝜂∇𝐿(𝜃𝑡−1′)
𝑚𝑡 = 𝜆𝑚𝑡−1 + 𝜂∇𝐿(𝜃𝑡−1′)
SGDM:
𝜃𝑡 = 𝜃𝑡−1 − 𝑚𝑡
𝑚𝑡 = 𝜆𝑚𝑡−1 + 𝜂∇𝐿(𝜃𝑡−1)
or
𝜃𝑡 = 𝜃𝑡−1 − 𝜆𝑚𝑡−1-𝜂∇𝐿(𝜃𝑡−1)
𝑚𝑡 = 𝜆𝑚𝑡−1 + 𝜂∇𝐿(𝜃𝑡−1)
Nadam [Dozat, ICLR workshop’16]
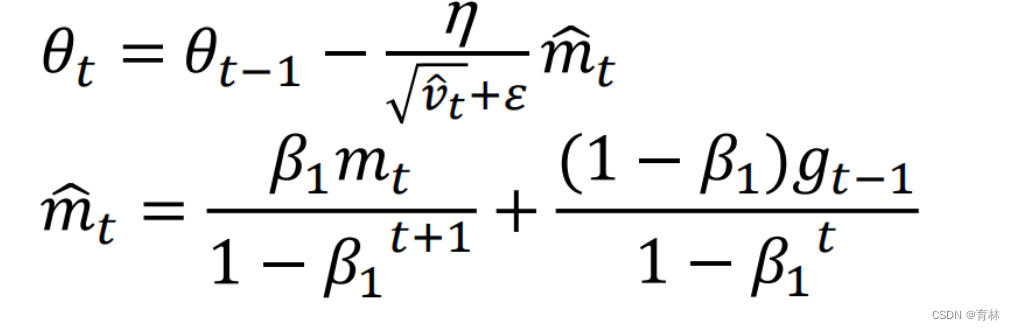
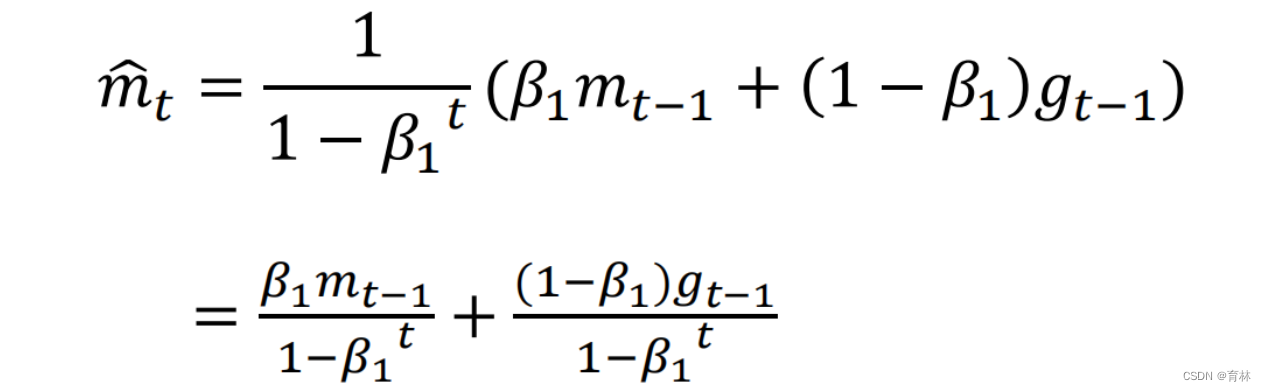
五、optimizer
L2
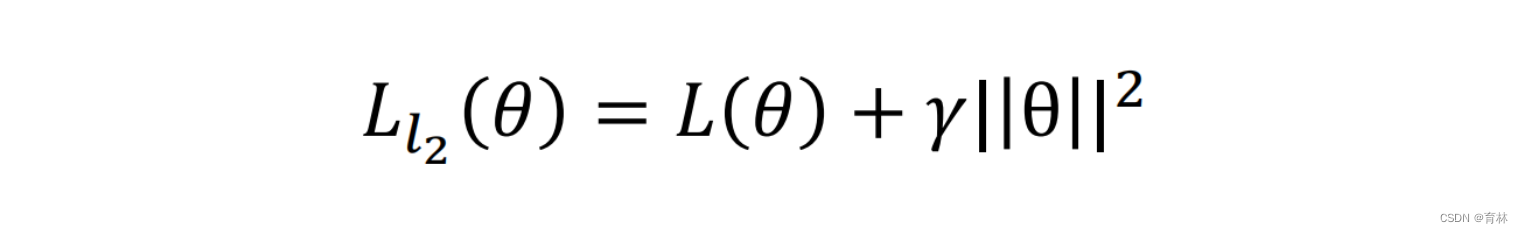
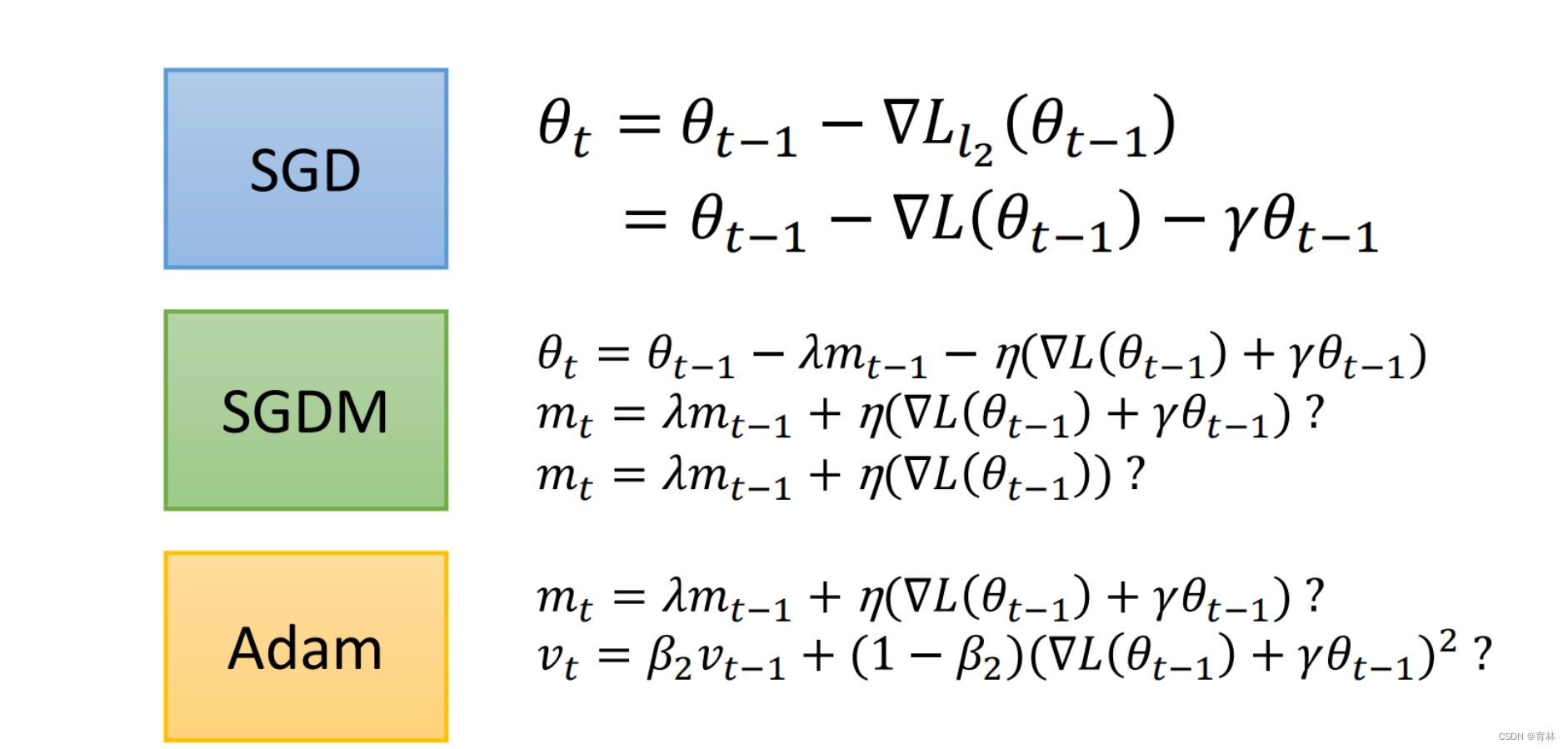
AdamW & SGDW with momentum
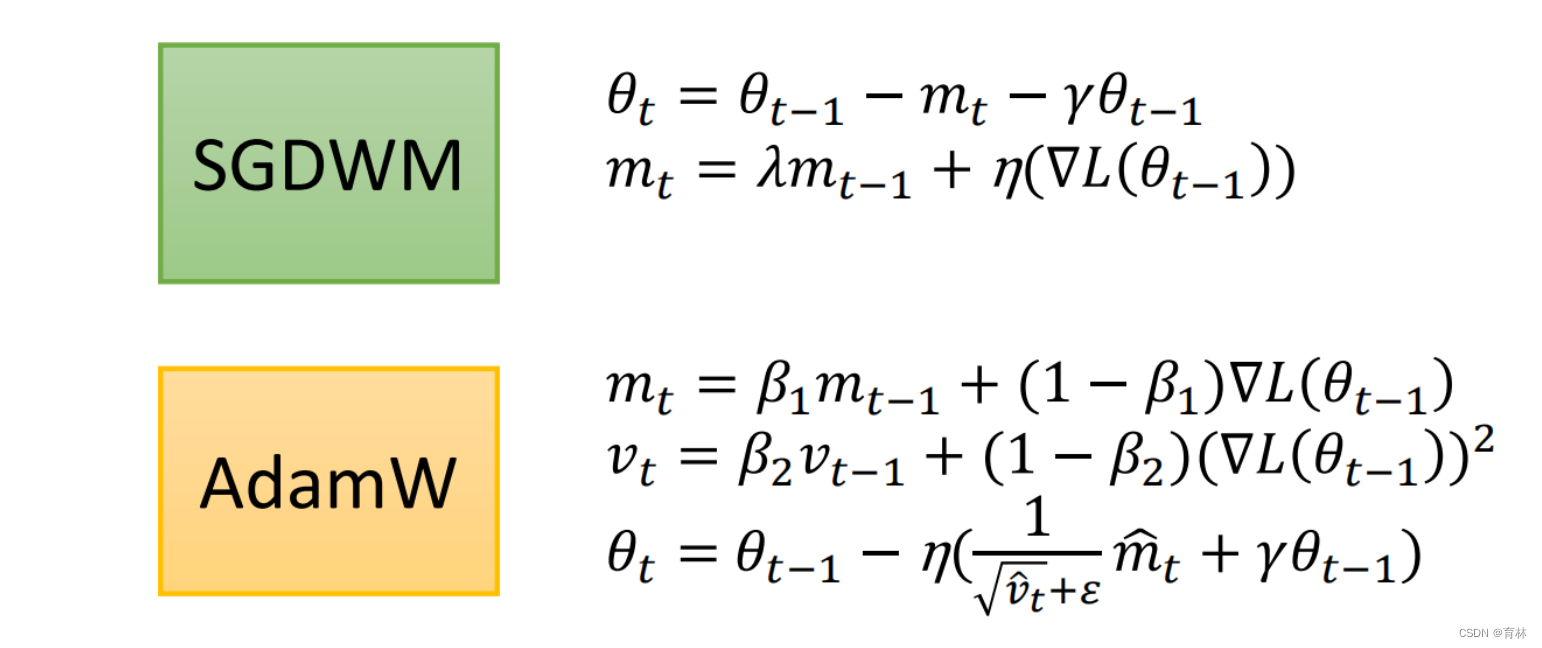
Something helps optimization
Normalization
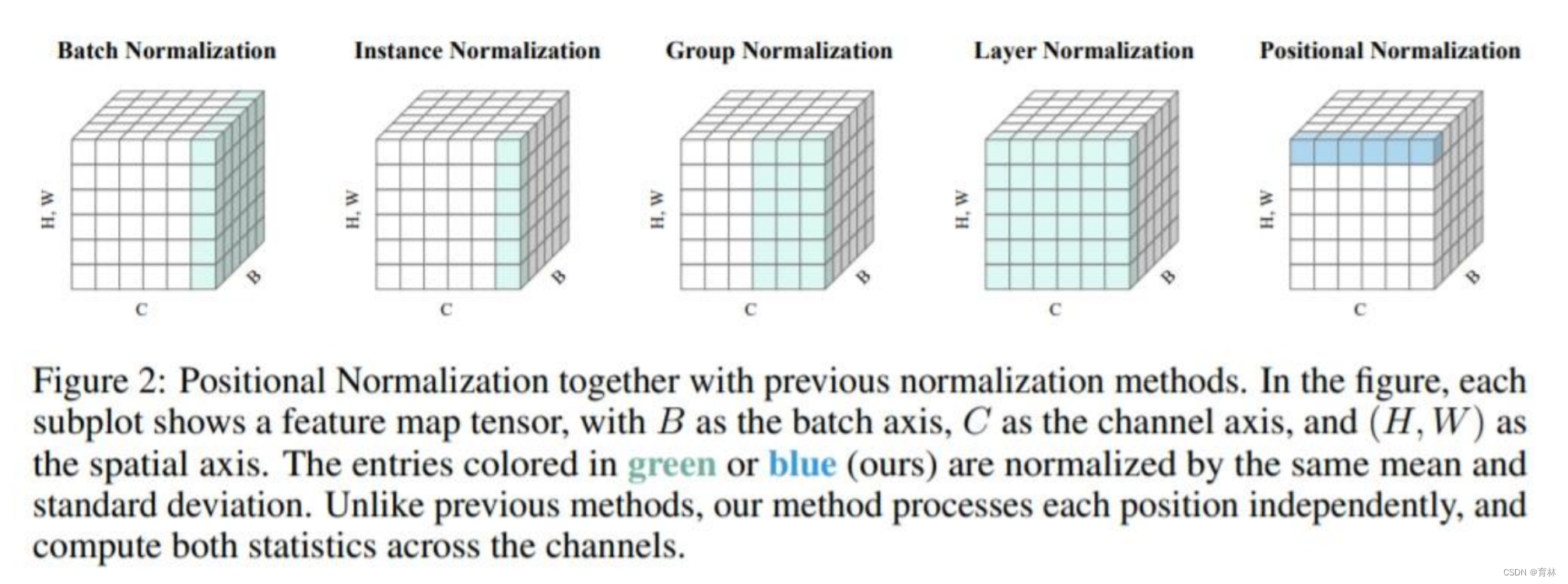
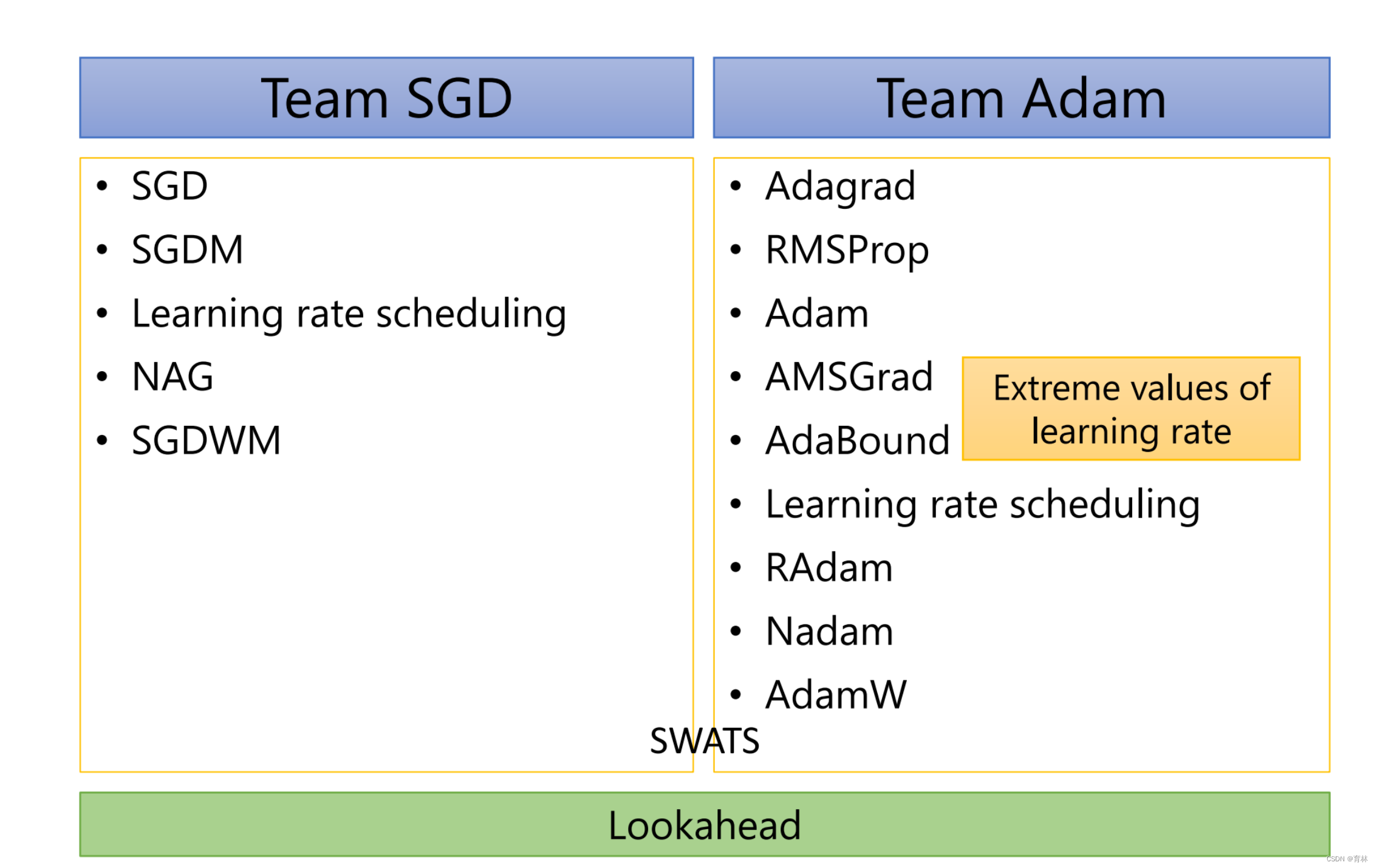
总结

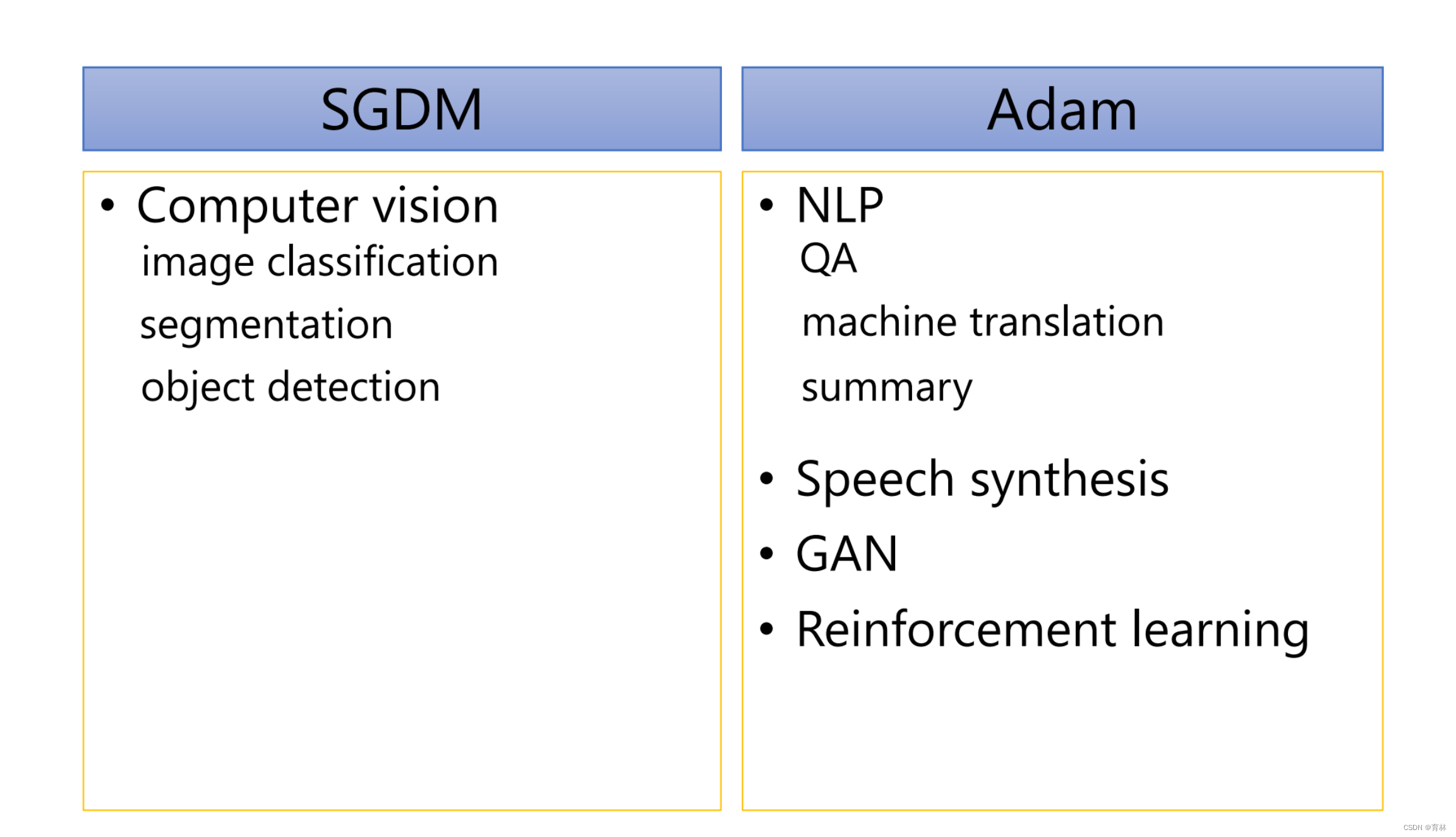
Advices:
![[洛谷-P3047] [USACO12FEB]Nearby Cows G(树形DP+换根DP)](https://img-blog.csdnimg.cn/5aa58266b0e548fa9ba3f5dbc44234c7.png)