【2】Dijkstra与SPFA等常见最短路算法的分析与比较——Bellman-Ford与SPFA

news2024/11/25 8:19:17

合集目录：

前言

一、Dijkstra

二、Bellman-Ford与SPFA（本文）

三、Dijkstra与SPFA的比较

四、Floyd

五、启发式搜索

Bellman-Ford

1. 算法介绍

The algorithm was first proposed by Alfonso Shimbel (1955), but is instead named after Richard Bellman and Lester Ford Jr., who published it in 1958 and 1956, respectively. Edward F. Moore also published a variation of the algorithm in 1959, and for this reason it is also sometimes called the Bellman–Ford–Moore algorithm. ——WIKIPEDIA

Bellman-Ford算法也是用于解决单源最短路问题，不过与Dijkstra不同的是，它可以解决带有负权边的单源最短路。Bellman-Ford算法通过限制经过边的数量，对每一条边都进行松弛，从而逐步得到最优解。

在一个 n n n个点的图中，任意两个点之间的最短路径最多有 n − 1 n-1 n−1条边（暂不考虑负环）。我们还是构造一个 d i s [ i ] dis[i] dis[i]数组，表示源点 s s s到点 i i i的最短距离。在算法最外层有一个 n − 1 n-1 n−1层的循环，第 i i i层循环表示从源点 s s s至某点 k k k的最短距离最多只经过 i i i条边。在此前提下，在第 n − 1 n-1 n−1层我们就能得到答案。同时，我们对 d i s dis dis数组进行划分层次， d i s i dis^i disi表示第 i i i层的 d i s dis dis数组。接下来考虑如何更新 d i s dis dis数组。当 i = 1 i=1 i=1时， d i s i [ k ] = w [ s ] [ k ] dis^i[k]=w[s][k] disi[k]=w[s][k]（ w [ s ] [ k ] w[s][k] w[s][k]为点 s s s至点 k k k的边的长度）；在每次循环中，我们依次遍历每条边，记某条边的起点和终点分别为 a a a和 b b b，通过这条边来更新 b b b点的 d i s dis dis数组，也就是“松弛”操作，即 d i s i [ k ] = m i n ( d i s i − 1 [ k ] , d i s i − 1 + w [ a ] [ b ] ) dis^i[k]=min(dis^{i-1}[k], dis^{i-1}+w[a][b]) disi[k]=min(disi−1[k],disi−1+w[a][b])。

以洛谷P3371 【模板】单源最短路径（弱化版）为例（70pts，不能通过全部测试点）：

#include <bits/stdc++.h>
#define A 500010

using namespace std;
int n, m, s, a[A], b[A];
long long dis[A], c[A];
void Bellman_ford(int s) {
	for (int i = 1; i <= n; i++) dis[i] = pow(2, 31) - 1;
	dis[s] = 0;
	for (int i = 1; i < n; i++)
		for (int j = 1; j <= m; j++)
			if (dis[b[j]] > dis[a[j]] + c[j])
				dis[b[j]] = dis[a[j]] + c[j];
}

int main(int argc, char const *argv[]) {
	cin >> n >> m >> s;
	for (int i = 1; i <= m; i++) scanf("%d%d%lld", &a[i], &b[i], &c[i]);
	Bellman_ford(s);
	for (int i = 1; i <= n; i++) printf("%lld ", dis[i]);
}

通过循环可以看出，Bellman-Ford的时间复杂度为 Θ ( n ⋅ m ) \Theta{(n·m)} Θ(n⋅m)。

2. 算法常见优化

在实际问题中，Bellman-Ford算法一般不需要做 n − 1 n-1 n−1层松弛操作就能得到最优解，因为最短路径经过的点数往往没有那么多，所以我们可以在某次循环不再进行松弛操作时，就直接退出循环。

for (int i = 1; i < n; i++) {
	bool check = 0;
	for (int j = 1; j <= m; j++)
		if (dis[b[j]] > dis[a[j]] + c[j])
			dis[b[j]] = dis[a[j]] + c[j], check = 1;
	if (!check) break;
}

对代码做了这个小小的改动后，就可以通过上面的题目了。
另外还有队列优化，也就是SPFA，会在下文着重讲解。

3. 判断负环

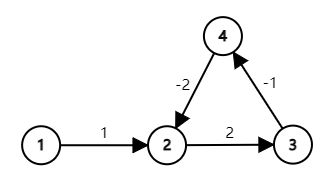
在这里插入图片描述
在这个图中，我们可以注意到有一个环，而且环中边权的和为负数，这就说明我们可以在环上走无数多次来达到更小的距离。这种情况下，最短路径是不存在的。在Bellman-Ford中，就体现为：第 n n n次松弛操作仍可得到更优的解。故可以通过下面的方式判断负环：

void Bellman_ford(int s) {
	for (int i = 1; i <= n; i++) dis[i] = pow(2, 31) - 1;
	dis[s] = 0;
	for (int i = 1; i < n; i++) {
		bool check = 0;
		for (int j = 1; j <= m; j++)
			if (dis[b[j]] > dis[a[j]] + c[j])
				dis[b[j]] = dis[a[j]] + c[j], check = 1;
		if (!check) break;
	}
	for (int j = 1; j <= m; j++)
		if (dis[b[j]] > dis[a[j]] + c[j]) {
			puts("Negative ring");
			return;
		}
}

4. 其他

Bellman-Ford算法容易理解且容易书写，但缺点就在于算法时间复杂度太高，所以在算法竞赛中很少见到它的身影。而它的队列优化版本SPFA，由于有着在稀疏随机图中优秀的时间复杂度，在算法竞赛中就较为重要。

SPFA

1. 算法介绍

可以确定，松弛操作必定只会发生在最短路径前导节点松弛成功的节点上，所以我们只用松弛成功的点在下一轮进行松弛，用一个队列记录松弛过的节点，避免了大量冗余计算。用一个 v i s [ i ] vis[i] vis[i]数组记录点 i i i是否在队列 q q q中，队列 q q q中是上一轮松弛成功的点，每次取出队列的队首，再用这个点进行松弛。

这是Bellman-Ford的队列优化版本，这种优化方式在1959年由Edward F. Moore作为广度优先搜索的扩展发表，所以也被称为Bellman-Ford-Moore算法。相同算法在1994年由段凡丁重新发现，他之前没有看过Moore的论文，所以给这种算法起了个通俗易懂的名字：Shortest Path Fast Algorithm。

#include <bits/stdc++.h>
#define A 1000010

using namespace std;
struct node{int next, to, w;}e[A];
int head[A], num;
void add(int fr, int to, int w) {
    e[++num].next = head[fr]; e[num].to = to;
    e[num].w = w; head[fr] = num;
}
int dis[A], n, m, s; bool vis[A];
void spfa(int s) {
    memset(vis, 0, sizeof vis); for (int i = 1; i <= n; i++) dis[i] = INT_MAX;
    dis[s] = 0; vis[s] = 1; queue<int> q; q.push(s);
    while (!q.empty()) {
        int fr = q.front(); q.pop(); vis[fr] = 0; // 将队首元素取出队列
        for (int i = head[fr]; i; i = e[i].next) {
            int ca = e[i].to;
            if (dis[ca] > dis[fr] + e[i].w) {
                dis[ca] = dis[fr] + e[i].w;
                if (!vis[ca]) vis[ca] = 1, q.push(ca); // 将松弛成功的点加入队列
            }
        }
    }
}

int main(int argc, char const *argv[]) {
    cin >> n >> m >> s;
    for (int i = 1; i <= m; i++) {
        int a, b, c; scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    spfa(s);
    for (int i = 1; i <= n; i++) printf("%d ", dis[i]);
}

2. 常见优化

这两种优化方式都使用了deque双端队列。
（1）SLF优化（Small Label First）
直译过来是：小的元素放前面。类似堆优化的Dijkstra，优先松弛距离较小的点。

void spfa_SLF(int s) {
    memset(vis, 0, sizeof vis); for (int i = 1; i <= n; i++) dis[i] = INT_MAX;
    dis[s] = 0; vis[s] = 1; deque<int> q; q.push_back(s);
    while (!q.empty()) {
        int fr = q.front(); q.pop_front(); vis[fr] = 0;
        for (int i = head[fr]; i; i = e[i].next) {
            int ca = e[i].to;
            if (dis[ca] > dis[fr] + e[i].w) {
                dis[ca] = dis[fr] + e[i].w;
                if (!vis[ca]) {
                    vis[ca] = 1;
                    if (q.empty() or dis[ca] > dis[q.front()]) q.push_back(ca);
                    else q.push_front(ca);
                }
            }
        }
    }
}

（2）LLL优化（Large Label Last）
直译过来是：大的元素放后面。LLL引入了平均值，距离大于平均值的节点会被移到队列尾端。前面的SLF是对入队做优化，LLL是对出队做优化，所以两者的说法并无冲突。

void spfa_LLL(int s) {
    memset(vis, 0, sizeof vis); for (int i = 1; i <= n; i++) dis[i] = INT_MAX;
    dis[s] = 0; vis[s] = 1; deque<int> q; q.push_back(s); int cnt = 1, sum = 0;
    while (!q.empty()) {
        int fr = q.front(); q.pop_front();
        cnt--; sum -= dis[fr];
        if (dis[fr] * cnt > sum) {
            q.push_back(fr);
            cnt++; sum += dis[fr];
            continue;
        }
        vis[fr] = 0; 
        for (int i = head[fr]; i; i = e[i].next) {
            int ca = e[i].to;
            if (dis[ca] > dis[fr] + e[i].w) {
                dis[ca] = dis[fr] + e[i].w;
                if (!vis[ca]) {
                    vis[ca] = 1;
                    q.push_back(ca);
                    cnt++; sum += dis[ca];
                }
            }
        }
    }
}

（3）SLF+LLL优化
前面也说到两种优化并无冲突，所以可以结合起来使用，出队使用LLL，入队使用SLF。
这两种优化算法大都是直观的理解，为此我找到了LLL优化的论文出处，论文中做了数值实验，详细介绍了几种优化算法。
原论文：Parallel_asynchronous_label-correcting_methods_for_shortest_paths
（4）MinPoP优化
这个是我在翻论文时看到的，这篇论文以SPFA为基础，将新提出的这个优化算法与SLF优化进行比较。原文中也提到了，“the improved algorithm is a little more efficient than SPFA and its SLF optimization algorithm”，提升并不是很大。原论文：An_Improved_SPFA_Algorithm_for_Single-Source_Shortest_Path_Problem_Using_Forward_Star_Data_Structure

void spfa_MinPoP(int s) { // 根据伪代码写的代码
	memset(vis, 0, sizeof vis); for (int i = 1; i <= n; i++) dis[i] = INT_MAX;
	dis[s] = 0; vis[s] = 1; deque<int> q; q.push_back(s); int minn = INT_MAX;
	while (!q.empty()) {
		int p = 0;
		int fr = q.front(); q.pop_front();
		vis[fr] = 0;
		for (int i = head[fr]; i; i = e[i].next) {
			int ca = e[i].to;
			if (dis[ca] > dis[fr] + e[i].w) {
				dis[ca] = dis[fr] + e[i].w;
				if (!vis[ca]) vis[ca] = 1, q.push_back(ca);
				if (dis[ca] < minn) minn = dis[ca], p = ca;
			}
		}
		if (p) q.push_front(p), vis[p] = 1;
	}
}

3. 判断负环

类比Bellman-Ford的判断负环的方法， 一个点最多被松弛 n − 1 n-1 n−1次，否则就一定存在负环。
洛谷P3385 【模板】负环：

#include <bits/stdc++.h>
#define A 10010

using namespace std;
struct node{int next, to, w;}e[A];
int head[A], num;
void add(int fr, int to, int w) {
    e[++num].next = head[fr]; e[num].to = to;
    e[num].w = w; head[fr] = num;
}
int dis[A], n, m, s, cnt[A]; bool vis[A];
void spfa(int s) {
    memset(vis, 0, sizeof vis); for (int i = 1; i <= n; i++) dis[i] = INT_MAX;
    dis[s] = 0; vis[s] = 1; queue<int> q; q.push(s);
    while (!q.empty()) {
        int fr = q.front(); q.pop(); vis[fr] = 0;
        for (int i = head[fr]; i; i = e[i].next) {
            int ca = e[i].to;
            if (dis[ca] > dis[fr] + e[i].w) {
                dis[ca] = dis[fr] + e[i].w;
                if (!vis[ca]) {
                	if (++cnt[ca] >= n) {
                		puts("YES");
                		return;
                	}
                	vis[ca] = 1, q.push(ca);
                }
            }
        }
    }
    puts("NO");
}

int main(int argc, char const *argv[]) {
	int T; cin >> T;
	while (T--) {
	    cin >> n >> m;
	    memset(head, 0, sizeof head); num = 0;
	    memset(cnt, 0, sizeof cnt);
	    for (int i = 1; i <= m; i++) {
	        int a, b, c; scanf("%d%d%d", &a, &b, &c);
	        if (c >= 0) add(a, b, c), add(b, a, c);
	        else add(a, b, c);
	    }
	    spfa(1);
	}
}

4. 时间复杂度

SPFA的最坏时间复杂度与Bellman-Ford相同，可以在特殊数据（网格图、菊花图等）下达到 Θ ( n ⋅ m ) \Theta{(n·m)} Θ(n⋅m)，可以将其看成是Bellman-Ford算法的特例情况，并没有对算法实质上的优化，所以有一些人不会承认SPFA。

5. 争议

在NOI2018D1T1归程中，出题人构造了特殊的数据，使得使用SPFA的选手从可以100分到了60分，并且在讲解题目时提出了“关于SPFA，它死了”这种说法。
SPFA
这道题目当时在OI界引起了很大的争议，在这之后，如何构造出卡SPFA的数据被越来越多人熟知，也有人逐一卡掉了SPFA的优化算法，其实一切的根源还是SPFA的假复杂度。所以说正权图最好还是用堆优化Dijkstra。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/403459.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

哪个牌子的洗地机耐用？耐用的洗地机推荐

哪个牌子的洗地机耐用？耐用的洗地机推荐

作为当下非常热销的洗地机&#xff0c;它不仅解放了双手&#xff0c;使用也非常的便捷。是生活品质提高的最好代表&#xff0c;但是面对市面上让人眼花缭乱的洗地机&#xff0c;挑选几个来回都决定不了到底入手哪个好&#xff01;为了能帮助大家选购到合适的洗地机&#xff0c;…
阅读更多...
gcc 编译的过程

gcc 编译的过程

#include <stdio.h> #define PI 3.14 int main(int argc, char const *argv[]) { //打印IP的值printf("PI %lf\n", PI);return 0; }编译的过程&#xff1a;预处理、编译、汇编、链接1.预处理&#xff1a;宏替换、删除注释、头文件包含、条件编译 -E &#xf…
阅读更多...
问心 | 再看token、session和cookie

问心 | 再看token、session和cookie

什么是cookie HTTP Cookie&#xff08;也叫 Web Cookie或浏览器 Cookie&#xff09;是服务器发送到用户浏览器并保存在本地的一小块数据&#xff0c;它会在浏览器下次向同一服务器再发起请求时被携带并发送到服务器上。 什么是session Session 代表着服务器和客户端一次会话…
阅读更多...
Paddle项目调试记录

Paddle项目调试记录

PaddlePaddle是百度公司提出的深度学习框架。近年来深度学习在很多机器学习领域都有着非常出色的表现&#xff0c;在图像识别、语音识别、自然语言处理、机器人、网络广告投放、医学自动诊断和金融等领域有着广泛应用。面对繁多的应用场景&#xff0c;深度学习框架有助于建模者…
阅读更多...
MyBatis-Plus(狂神)

MyBatis-Plus(狂神)

一.特点 无侵入&#xff1a;只做增强不做改变&#xff0c;引入它不会对现有工程产生影响&#xff0c;如丝般顺滑损耗小&#xff1a;启动即会自动注入基本 CURD&#xff0c;性能基本无损耗&#xff0c;直接面向对象操作强大的 CRUD 操作&#xff1a;内置通用 Mapper、通用 Serv…
阅读更多...
GDB调试快速入门

GDB调试快速入门

什么是GDB&#xff1a; GDB - - - (GNU symbolic debugger)是Linux平台下最常用的一款程序调试器。 自己的Linux是否安装GDB? 一般来说&#xff0c;使用Ubuntu的话&#xff0c;系统就会自带的有GDB调试器的 命令窗口输入如下命令可以查看是否安装了gdb&#xff1a; gdb -v …
阅读更多...
制作一个简单的信用卡验证表

制作一个简单的信用卡验证表

下载：https://download.csdn.net/download/mo3408/87559584 效果图： 您可以从文章顶部附近的下载按钮获取该项目的完整代码。这些文件的概述如下所示： 我们需要将两个 .css 文件和两个 .js 文件包含在我们的 HTML 中。所有其他资源，例如 Bootstrap 框架、jQuery 和 Web 字…
阅读更多...
SecureCRT 安装并绑定ENSP设备终端

SecureCRT 安装并绑定ENSP设备终端

软件下载链接链接&#xff1a;https://pan.baidu.com/s/1WFxmQgaO9bIiUTwBLSR4OA?pwd2023 提取码&#xff1a;2023 CRT安装&#xff1a;软件可以从上面链接进行下载&#xff0c;下载完成后解压如下&#xff1a;首先双击运行scrt-x64.8.5.4 软件&#xff0c;进行安装点击NEXT选…
阅读更多...
PMP项目管理项目资源管理

PMP项目管理项目资源管理

目录1 项目资源管理概述2 规划资源管理3 估算活动资源4 获取资源5 建设团队6 管理团队7 控制资源1 项目资源管理概述 项目资源管理包括识别、获取和管理所需资源以成功完成项目的各个过程&#xff0c;这些过程有助于确保项目经理和项目团队在正确的时间和地点使用正确的资源。…
阅读更多...
Nacos未授权访问漏洞（CVE-2021-29441）

Nacos未授权访问漏洞（CVE-2021-29441）

目录漏洞描述影响范围环境搭建漏洞复现声明&#xff1a;本文仅供学习参考&#xff0c;其中涉及的一切资源均来源于网络&#xff0c;请勿用于任何非法行为&#xff0c;否则您将自行承担相应后果&#xff0c;本人不承担任何法律及连带责任。加粗样式 漏洞描述 Nacos 是阿里巴巴…
阅读更多...
Redis缓存双写一致性

Redis缓存双写一致性

目录双写一致性Redis与Mysql双写一致性canal配置流程代码案例双写一致性理解缓存操作细分缓存一致性多种更新策略挂牌报错,凌晨升级先更新数据库,在更新缓存先删除缓存,在更新数据库先更新数据库,在删除缓存延迟双删策略总结双写一致性 Redis与Mysql双写一致性 canal 主要是…
阅读更多...
vuex3的介绍与state、actions和mutations的使用

vuex3的介绍与state、actions和mutations的使用

一、定义官网&#xff1a;Vuex 是什么&#xff1f; | Vuex (vuejs.org)Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态&#xff0c;并以相应的规则保证状态以一种可预测的方式发生变化。二、安装cdn<script src"/path/…
阅读更多...
[手撕数据结构]栈的深入学习-java实现

[手撕数据结构]栈的深入学习-java实现

CSDN的各位uu们你们好,今天千泽带来了栈的深入学习,我们会简单的用代码实现一下栈, 接下来让我们一起进入栈的神奇小世界吧!0.速览文章一、栈的定义1. 栈的概念2. 栈的图解二、栈的模拟实现三.栈的经典使用场景-逆波兰表达式总结一、栈的定义 1. 栈的概念 栈&#xff1a;一种…
阅读更多...
Optimizers for Deep Learning

Optimizers for Deep Learning

文章目录一、Some NotationsWhat is Optimization about?二、SGDSGD with Momentum(SGDM)Why momentum?三、AdagradRMSProp四、AdamSWATS [Keskar, et al., arXiv’17]Towards Improving AdamTowards Improving SGDMRAdam vs SWATSLookahead [Zhang, et al., arXiv’19]Momen…
阅读更多...
[洛谷-P3047] [USACO12FEB]Nearby Cows G（树形DP+换根DP）

[洛谷-P3047] [USACO12FEB]Nearby Cows G（树形DP+换根DP）

[洛谷-P3047] [USACO12FEB]Nearby Cows G一、问题题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示二、分析1、状态表示2、状态转移3、换根DP三、代码一、问题 题目描述 Farmer John has noticed that his cows often move between nearby fields. Taking this in…
阅读更多...
【数据结构初阶】单链表面试题|内含链表带环问题

【数据结构初阶】单链表面试题|内含链表带环问题

目录 前言 链表面试题 1. 删除链表中等于给定值 val 的所有节点。oj链接 2.反转一个单链表。oj链接 3. 给定一个带有头结点 head 的非空单链表&#xff0c;返回链表的中间结点。如果有两个中间结点&#xff0c;则返回第二个中间结点。oj链接 4. 输入一个链表&#xff0c;…
阅读更多...
每天五分钟机器学习算法：贝叶斯算法中处理重复词语的三种方式

每天五分钟机器学习算法：贝叶斯算法中处理重复词语的三种方式

什么是重复词语？ 我们预测一封邮件是否是垃圾邮件，前面已经介绍，我们需要对其进行分词处理，问题是分词处理之后很有可能有重复的词，那么这重复的词如何处理，这里我们介绍三种方式： 1.多项式模型 2.伯努利模型 3.混合模型 重复的情况举例 现在有一个垃圾邮件，它的内…
阅读更多...
安装Linux虚拟机和Hadoop平台教程汇总及踩坑总结

安装Linux虚拟机和Hadoop平台教程汇总及踩坑总结

&#x1f4cd;主要内容介绍安装Linux虚拟机、ubuntu系统、安装hadoop三个环节的教程链接介绍及本机与虚拟机的FTP传输教程总结&#xff08;直接找hadoop安装环节的5.filezilla传输文件&#xff09;新鲜出炉的踩坑总结和填坑指南安装Linux虚拟机和ubuntu系统一、材料和工具1、下…
阅读更多...
站内SEO内容优化包括那些？

站内SEO内容优化包括那些？

站内SEO优化是指优化网站内部结构&#xff0c;以提高搜索引擎对网站的识别和评价&#xff0c;从而提高网站在搜索引擎自然排名中的权重和位置。 站内SEO内容优化的目标是提高网站内容的质量和相关性&#xff0c;从而吸引更多的用户访问和留存。 以下是一些站内SEO优化的要点&…
阅读更多...
Yolov5-交通标志检测与识别

Yolov5-交通标志检测与识别

项目介绍 上一篇文章介绍了基于卷积神经网络的交通标志分类识别Python交通标志识别基于卷积神经网络的保姆级教程&#xff08;Tensorflow&#xff09;&#xff0c;并且最后实现了一个pyqt5的GUI界面&#xff0c;并且还制作了一个简单的Falsk前端网页实现了前后端的一个简单交互…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023