一、问题

题目描述

Farmer John has noticed that his cows often move between nearby fields. Taking this into account, he wants to plant enough grass in each of his fields not only for the cows situated initially in that field, but also for cows visiting from nearby fields.

Specifically, FJ’s farm consists of N fields (1 <= N <= 100,000), where some pairs of fields are connected with bi-directional trails (N-1 of them in total). FJ has designed the farm so that between any two fields i and j, there is a unique path made up of trails connecting between i and j. Field i is home to C(i) cows, although cows sometimes move to a different field by crossing up to K trails (1 <= K <= 20).

FJ wants to plant enough grass in each field i to feed the maximum number of cows, M(i), that could possibly end up in that field – that is, the number of cows that can potentially reach field i by following at most K trails. Given the structure of FJ’s farm and the value of C(i) for each field i, please help FJ compute M(i) for every field i.

输入格式

* Line 1: Two space-separated integers, N and K.

* Lines 2…N: Each line contains two space-separated integers, i and j (1 <= i,j <= N) indicating that fields i and j are directly connected by a trail.

* Lines N+1…2N: Line N+i contains the integer C(i). (0 <= C(i) <= 1000)

第一行两个正整数 $n, k$ 。
接下来 $n - 1$ 行，每行两个正整数 $u, v$ ，表示 $u, v$ 之间有一条边。
最后 $n$ 行，每行一个非负整数 $c_i$ ，表示点权。

输出格式

* Lines 1…N: Line i should contain the value of M(i).

输出 $n$ 行，第 $i$ 行一个整数表示 $m_i$ 。

样例 #1

样例输入 #1

样例输出 #1

提示

There are 6 fields, with trails connecting (5,1), (3,6), (2,4), (2,1), and (3,2). Field i has C(i) = i cows.

Field 1 has M(1) = 15 cows within a distance of 2 trails, etc.

【数据范围】
对于 $100\%$ 的数据： $\le n \le 10^5$ ， $\le k \le 20$ ， $\le c_i \le 1000$

二、分析

题目简单地来说就是：
给你一棵 $n$ 个点的树，点带权，对于每个节点求出距离它不超过 $k$ 的所有节点权值和 $m_i$ 。

对于树中的某个节点而言，距离它不超过 $k$ 的节点主要来源于两方面，一个是该节点的子节点中距离该节点不超过距离 $k$ 的节点的权值和，另一个就是该节点向上沿着父节点方向不超过距离 $k$ 的点的权值和。

对于子节点方向的节点的权值和，我们可以先通过普通的树形DP计算出来。

因此，我们先写一个DP计算出子树中距离该点不超过 $k$ 的点的权值和。

1、状态表示

$f [u] [k]$ 表示以 $u$ 为根节点的树中，距离 $u$ 不超过 $k$ 的子节点的权值和。

2、状态转移

$f[u][k]=val[u]+\sum f[son][k-1]$
到节点 $u$ 不超过距离 $k$ ，即距离 $so n$ 不超过 $k - 1$ ，然后加在一起即可。同时 $u$ 节点本身也是答案，因为 $u$ 节点本身是不超过距离 $0$ 的节点。

3、换根DP

这个题目本身是个无根树，如果我们认为规定编号为1的节点是根的话，那么对于祖宗节点 $1$ 来说， $f [1] [k]$ 就是距离 $1$ 节点不超过距离 $k$ 的节点的权值和。因为祖宗节点是没有父亲节点的，所以我们就不需要考虑沿着父节点方向的节点权值和。

我们不妨令： $g [u] [k]$ 表示所有到 $u$ 节点的不超过距离 $k$ 的节点的权值和。根据刚刚的分析： $g [1] [k] = f [1] [k]$

这个就是我们换根DP的初始化。其实受这个的启发，我们完全可以去把每个点都当作根，然后暴力跑出答案，但是这个暴力做法的时间复杂度是 $O(n^2)$ 的，会超时。

所以当我们将祖宗节点从节点1换为另一个节点的时候，我们只能通过数学上的关系来计算出 $g$ 数组元素的值。这个也是换根DP的意义。

我们看下面的图：
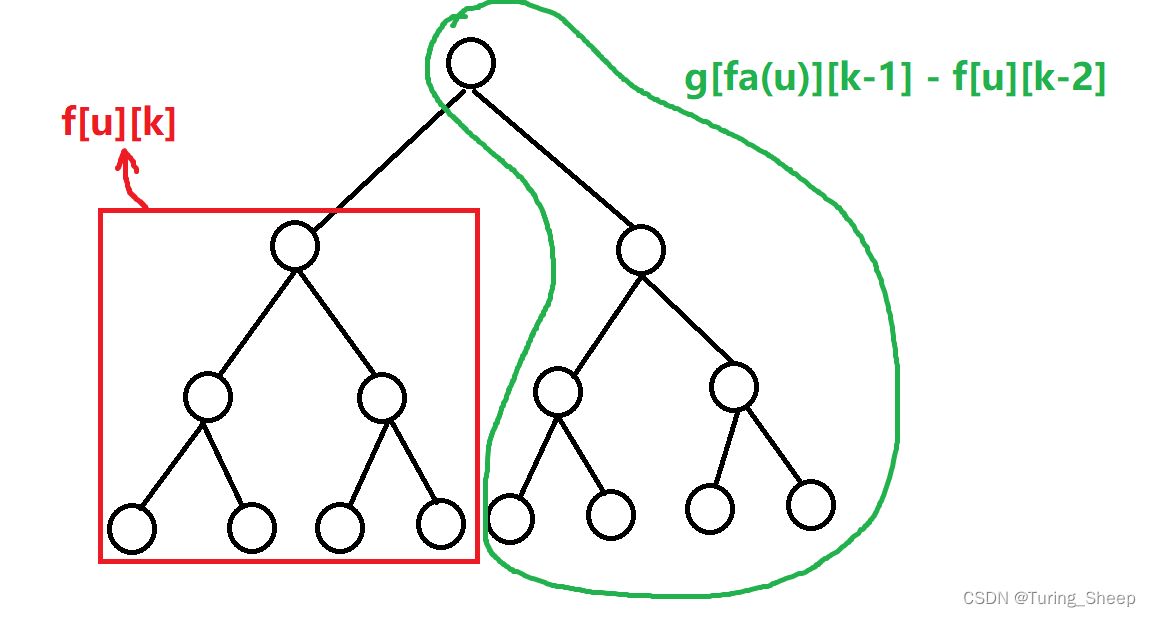
在这里插入图片描述
红色框是非常好理解的，直接写成 $f [u] [k]$ 即可。上面的部分，我们可以写成 $g [f a (u)] [k - 1]$ 。因为到 $u$ 不超过 $k$ 的距离，即距离它的父亲节点不超过 $k - 1$ 的距离。

但是这么写对吗？

答案是不对的， $g [f a (u)] [k - 1]$ 和 $f [u] [k]$ 是有重复部分的。我们需要减去这段重复的部分，那么关键问题是重复部分如何表示？

重复部分肯定是出现在了红色框中，红色框中到 $f a (u)$ 不超过距离 $k - 1$ ，即距离 $u$ 不超过 $k - 2$ ，同时重复部分又恰好是节点 $u$ 的子节点，所以这部分可以表示为： $f [u] [k - 2]$ 。

所以最终的结果就是：

$g [u] [k] = f [u] [k] + g [f a (u)] [k - 1] - f [u] [k - 2]$

但是上述方程成立的条件是 $k\geq 2$ 的。

所以我们还得想一想 $\leq 1$ 的时候。

如果 $k = 0$ ， $g [u] [0]$ 其实就是 $v a l [u]$ ，因为不超过距离 $0$ 的点只有本身。

如果 $k = 1$ ，那么 $g [u] [1]$ 其实就是 $f [u] [1] + v a l [f a (u)]$ ，因为沿着父节点方向距离 $u$ 不超过 $1$ 的点，只有父节点，而树中，父节点是唯一的。沿着子节点方向，其实就是 $u$ 的各个子节点，而这些子节点可以统统用 $f [u] [1]$ 表示。

三、代码

#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e5 + 10;
vector<int>edge[N];
int f[N][25], g[N][25];
int val[N];
int n, k;

void dp(int u, int father)
{
	for(int i = 0; i <= k; i ++)
		f[u][i] = val[u];
	for(int i = 0; i < edge[u].size(); i ++ )
	{
		int son = edge[u][i];
		if(son == father)
			continue;
		dp(son, u);

		for(int j = 1; j <= k; j ++ )
		{
			f[u][j] += f[son][j - 1];
		}
	}
	return;
}

void dp2(int u, int father)
{
	for(int i = 0; i < edge[u].size(); i ++ )
	{
		int son = edge[u][i];
		if(son == father)
			continue;
		g[son][0] = val[son];
		g[son][1] = f[son][1] + val[u];
		for(int j = 2; j <= k; j ++ )
		{
			g[son][j] = g[u][j - 1] + f[son][j] - f[son][j - 2]; 
		}
		
		dp2(son, u);
	}
}

void solve()
{
	cin >> n >> k;
	for(int i = 0; i < n - 1; i ++ )
	{
		int a, b;
		cin >> a >> b;
		edge[a].push_back(b);
		edge[b].push_back(a);
	}

	for(int i = 1; i <= n; i ++ )
		cin >> val[i];

	dp(1, 0);
	for(int i = 0; i <= k; i ++ )
	{
		g[1][i] = f[1][i];
	}
	dp2(1, 0);
	// for(int i = 1; i <= n; i ++ )
	// {
	// 	cout << f[i][k] << endl;
	// }
	// cout << endl;
	for(int i = 1; i <= n; i ++ )
	{
		cout << g[i][k] << endl;
	}
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	solve();
}